An improved convergence analysis for decentralized online stochastic non-convex optimization
Paper and Code
Aug 10, 2020
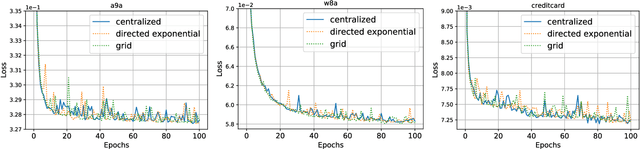
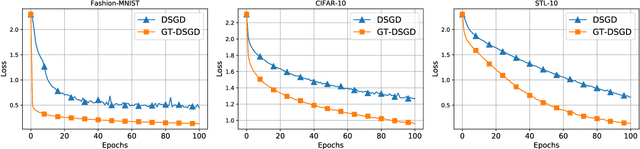
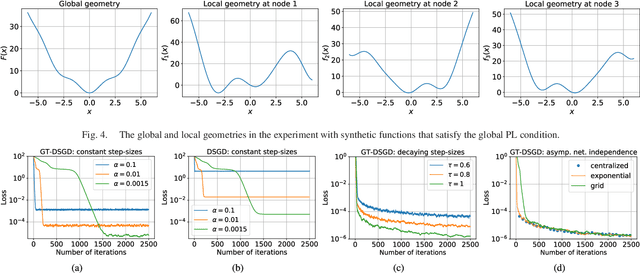
In this paper, we study decentralized online stochastic non-convex optimization over a network of nodes. Integrating a technique called gradient tracking in decentralized stochastic gradient descent (DSGD), we show that the resulting algorithm, GT-DSGD, exhibits several important characteristics towards minimizing a sum of smooth non-convex functions. The main results of this paper can be divided into two categories: (1) For general smooth non-convex functions, we establish a non-asymptotic characterization of GT-DSGD and derive the conditions under which it achieves network-independent performance and matches centralized minibatch SGD. In comparison, the existing results suggest that the performance of GT-DSGD is always network-dependent and is therefore strictly worse than that of centralized minibatch SGD. (2) When the global function additionally satisfies the Polyak-Lojasiewics condition, we derive the exponential stability range for GT-DSGD under a constant step-size up to a steady-state error. Under stochastic approximation step-sizes, we establish, for the first time, the optimal global sublinear convergence rate on almost every sample path, in addition to the convergence rate in mean. Since strongly convex functions are a special case of this class of problems, our results are not only immediately applicable but also improve the currently known best convergence rates and their dependence on problem parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge