Distributed Active State Estimation with User-Specified Accuracy
Paper and Code
Jan 14, 2018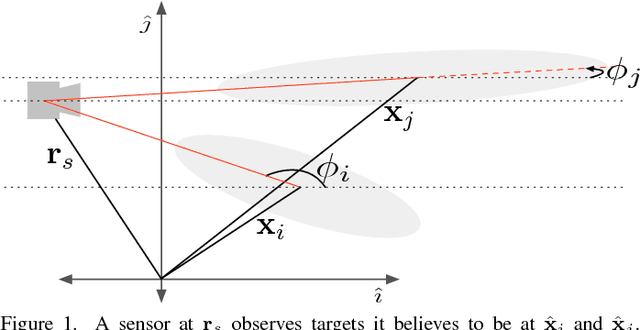
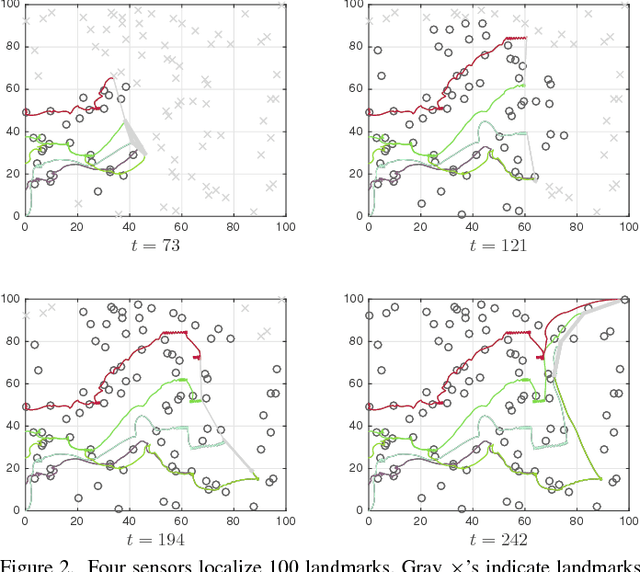
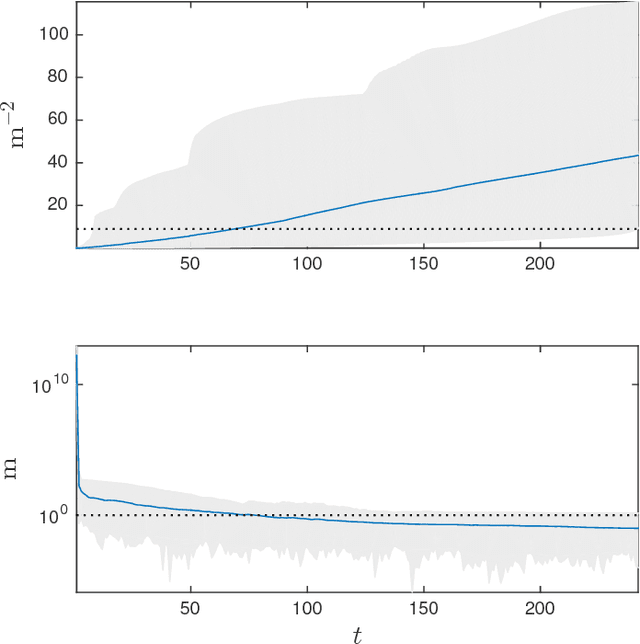
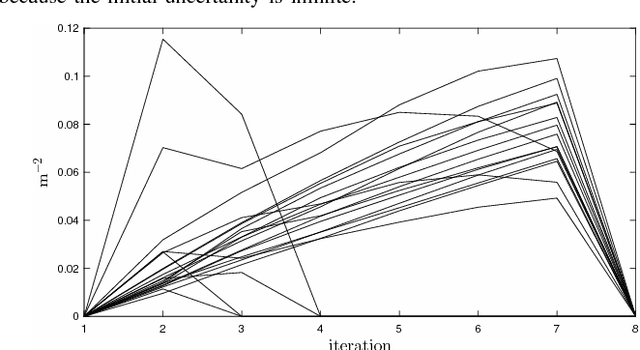
In this paper, we address the problem of controlling a network of mobile sensors so that a set of hidden states are estimated up to a user-specified accuracy. The sensors take measurements and fuse them online using an Information Consensus Filter (ICF). At the same time, the local estimates guide the sensors to their next best configuration. This leads to an LMI-constrained optimization problem that we solve by means of a new distributed random approximate projections method. The new method is robust to the state disagreement errors that exist among the robots as the ICF fuses the collected measurements. Assuming that the noise corrupting the measurements is zero-mean and Gaussian and that the robots are self localized in the environment, the integrated system converges to the next best positions from where new observations will be taken. This process is repeated with the robots taking a sequence of observations until the hidden states are estimated up to the desired user-specified accuracy. We present simulations of sparse landmark localization, where the robotic team achieves the desired estimation tolerances while exhibiting interesting emergent behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge