Optimal Bayesian Affine Estimator and Active Learning for the Wiener Model

This paper presents a Bayesian estimation framework for Wiener models, focusing on learning nonlinear output functions under known linear state dynamics. We derive a closed-form optimal affine estimator for the unknown parameters, characterized by the so-called "dynamic basis statistics (DBS)." Several features of the proposed estimator are studied, including Bayesian unbiasedness, closed-form posterior statistics, error monotonicity in trajectory length, and consistency condition (also known as persistent excitation). In the special case of Fourier basis functions, we demonstrate that the closed-form description is computationally available, as the Fourier DBS enjoys explicit expression. Furthermore, we identify an inherent inconsistency in single-trajectory measurements, regardless of input excitation. Leveraging the closed-form estimation error, we develop an active learning algorithm synthesizing input signals to minimize estimation error. Numerical experiments validate the efficacy of our approach, showing significant improvements over traditional regularized least-squares methods.

Interval Markov Decision Processes with Continuous Action-Spaces

Interval Markov Decision Processes (IMDPs) are uncertain Markov models, where the transition probabilities belong to intervals. Recently, there has been a surge of research on employing IMDPs as abstractions of stochastic systems for control synthesis. However, due to the absence of algorithms for synthesis over IMDPs with continuous action-spaces, the action-space is assumed discrete a-priori, which is a restrictive assumption for many applications. Motivated by this, we introduce continuous-action IMDPs (caIMDPs), where the bounds on transition probabilities are functions of the action variables, and study value iteration for maximizing expected cumulative rewards. Specifically, we show that solving the max-min problem associated to value iteration is equivalent to solving $|\mathcal{Q}|$ max problems, where $|\mathcal{Q}|$ is the number of states of the caIMDP. Then, exploiting the simple form of these max problems, we identify cases where value iteration over caIMDPs can be solved efficiently (e.g., with linear or convex programming). We also gain other interesting insights: e.g., in the case where the action set $\mathcal{A}$ is a polytope and the transition bounds are linear, synthesizing over a discrete-action IMDP, where the actions are the vertices of $\mathcal{A}$, is sufficient for optimality. We demonstrate our results on a numerical example. Finally, we include a short discussion on employing caIMDPs as abstractions for control synthesis.

Observational Robustness and Invariances in Reinforcement Learning via Lexicographic Objectives

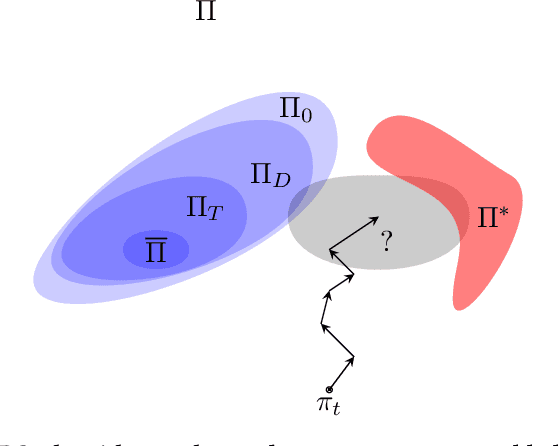
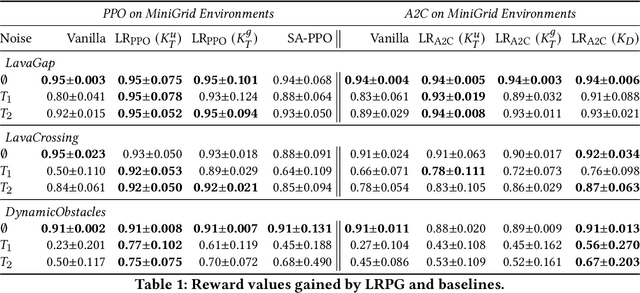
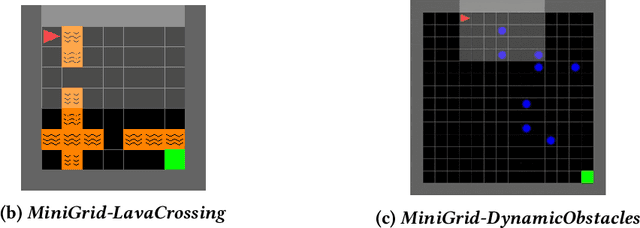
Policy robustness in Reinforcement Learning (RL) may not be desirable at any price; the alterations caused by robustness requirements from otherwise optimal policies should be explainable and quantifiable. Policy gradient algorithms that have strong convergence guarantees are usually modified to obtain robust policies in ways that do not preserve algorithm guarantees, which defeats the purpose of formal robustness requirements. In this work we study a notion of robustness in partially observable MDPs where state observations are perturbed by a noise-induced stochastic kernel. We characterise the set of policies that are maximally robust by analysing how the policies are altered by this kernel. We then establish a connection between such robust policies and certain properties of the noise kernel, as well as with structural properties of the underlying MDPs, constructing sufficient conditions for policy robustness. We use these notions to propose a robustness-inducing scheme, applicable to any policy gradient algorithm, to formally trade off the reward achieved by a policy with its robustness level through lexicographic optimisation, which preserves convergence properties of the original algorithm. We test the the proposed approach through numerical experiments on safety-critical RL environments, and show how the proposed method helps achieve high robustness when state errors are introduced in the policy roll-out.