Scalable Kernel Inverse Optimization

Inverse Optimization (IO) is a framework for learning the unknown objective function of an expert decision-maker from a past dataset. In this paper, we extend the hypothesis class of IO objective functions to a reproducing kernel Hilbert space (RKHS), thereby enhancing feature representation to an infinite-dimensional space. We demonstrate that a variant of the representer theorem holds for a specific training loss, allowing the reformulation of the problem as a finite-dimensional convex optimization program. To address scalability issues commonly associated with kernel methods, we propose the Sequential Selection Optimization (SSO) algorithm to efficiently train the proposed Kernel Inverse Optimization (KIO) model. Finally, we validate the generalization capabilities of the proposed KIO model and the effectiveness of the SSO algorithm through learning-from-demonstration tasks on the MuJoCo benchmark.

Inverse Optimization for Routing Problems

We propose a method for learning decision-makers' behavior in routing problems using Inverse Optimization (IO). The IO framework falls into the supervised learning category and builds on the premise that the target behavior is an optimizer of an unknown cost function. This cost function is to be learned through historical data, and in the context of routing problems, can be interpreted as the routing preferences of the decision-makers. In this view, the main contributions of this study are to propose an IO methodology with a hypothesis function, loss function, and stochastic first-order algorithm tailored to routing problems. We further test our IO approach in the Amazon Last Mile Routing Research Challenge, where the goal is to learn models that replicate the routing preferences of human drivers, using thousands of real-world routing examples. Our final IO-learned routing model achieves a score that ranks 2nd compared with the 48 models that qualified for the final round of the challenge. Our results showcase the flexibility and real-world potential of the proposed IO methodology to learn from decision-makers' decisions in routing problems.

Learning in Inverse Optimization: Incenter Cost, Augmented Suboptimality Loss, and Algorithms

In Inverse Optimization (IO), an expert agent solves an optimization problem parametric in an exogenous signal. From a learning perspective, the goal is to learn the expert's cost function given a dataset of signals and corresponding optimal actions. Motivated by the geometry of the IO set of consistent cost vectors, we introduce the "incenter" concept, a new notion akin to circumcenter recently proposed by Besbes et al. [2022]. Discussing the geometric and robustness interpretation of the incenter cost vector, we develop corresponding tractable convex reformulations, which are in contrast with the circumcenter, which we show is equivalent to an intractable optimization program. We further propose a novel loss function called Augmented Suboptimality Loss (ASL), as a relaxation of the incenter concept, for problems with inconsistent data. Exploiting the structure of the ASL, we propose a novel first-order algorithm, which we name Stochastic Approximate Mirror Descent. This algorithm combines stochastic and approximate subgradient evaluations, together with mirror descent update steps, which is provably efficient for the IO problems with high cardinality discrete feasible sets. We implement the IO approaches developed in this paper as a Python package called InvOpt. All of our numerical experiments are reproducible, and the underlying source code is available as examples in the InvOpt package.

Adaptive Online Optimization with Predictions: Static and Dynamic Environments

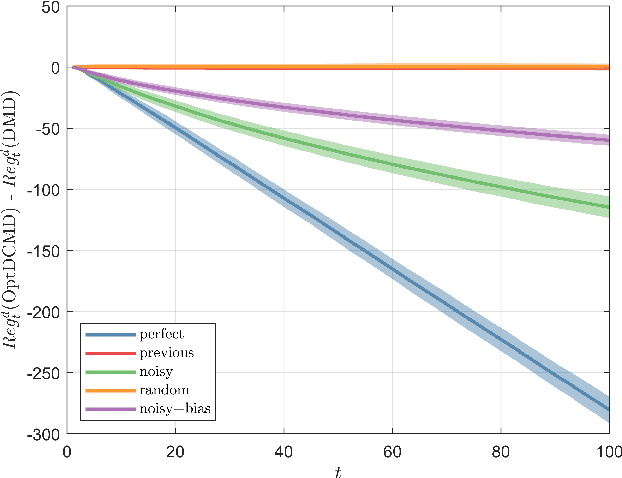
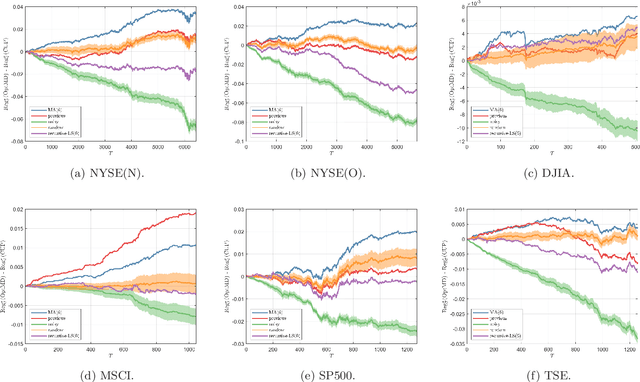
In the past few years, Online Convex Optimization (OCO) has received notable attention in the control literature thanks to its flexible real-time nature and powerful performance guarantees. In this paper, we propose new step-size rules and OCO algorithms that simultaneously exploit gradient predictions, function predictions and dynamics, features particularly pertinent to control applications. The proposed algorithms enjoy static and dynamic regret bounds in terms of the dynamics of the reference action sequence, gradient prediction error and function prediction error, which are generalizations of known regularity measures from the literature. We present results for both convex and strongly convex costs. We validate the performance of the proposed algorithms in a trajectory tracking case study, as well as portfolio optimization using real-world datasets.