Generalized maximum entropy estimation

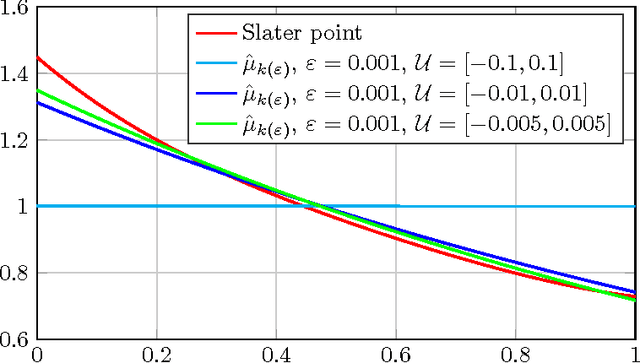
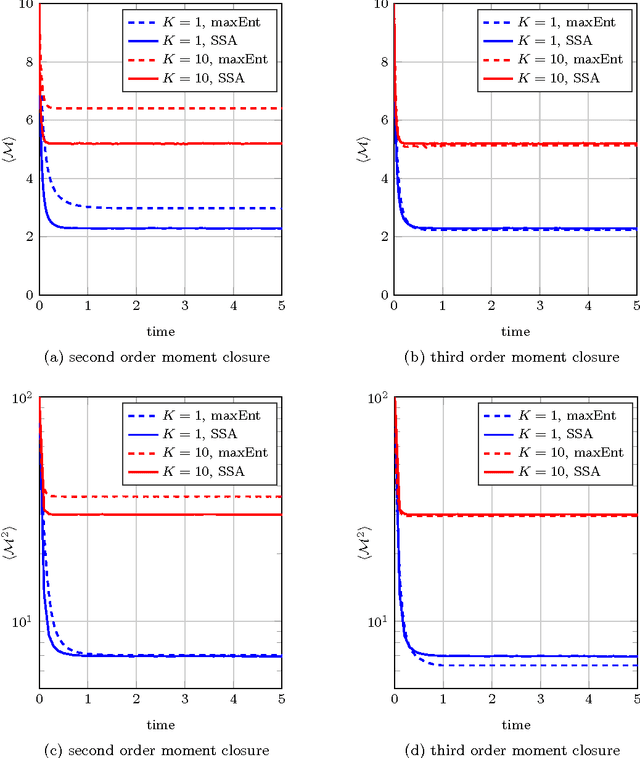
We consider the problem of estimating a probability distribution that maximizes the entropy while satisfying a finite number of moment constraints, possibly corrupted by noise. Based on duality of convex programming, we present a novel approximation scheme using a smoothed fast gradient method that is equipped with explicit bounds on the approximation error. We further demonstrate how the presented scheme can be used for approximating the chemical master equation through the zero-information moment closure method.