Generalization Through The Lens Of Leave-One-Out Error

Despite the tremendous empirical success of deep learning models to solve various learning tasks, our theoretical understanding of their generalization ability is very limited. Classical generalization bounds based on tools such as the VC dimension or Rademacher complexity, are so far unsuitable for deep models and it is doubtful that these techniques can yield tight bounds even in the most idealistic settings (Nagarajan & Kolter, 2019). In this work, we instead revisit the concept of leave-one-out (LOO) error to measure the generalization ability of deep models in the so-called kernel regime. While popular in statistics, the LOO error has been largely overlooked in the context of deep learning. By building upon the recently established connection between neural networks and kernel learning, we leverage the closed-form expression for the leave-one-out error, giving us access to an efficient proxy for the test error. We show both theoretically and empirically that the leave-one-out error is capable of capturing various phenomena in generalization theory, such as double descent, random labels or transfer learning. Our work therefore demonstrates that the leave-one-out error provides a tractable way to estimate the generalization ability of deep neural networks in the kernel regime, opening the door to potential, new research directions in the field of generalization.

The power of quantum neural networks

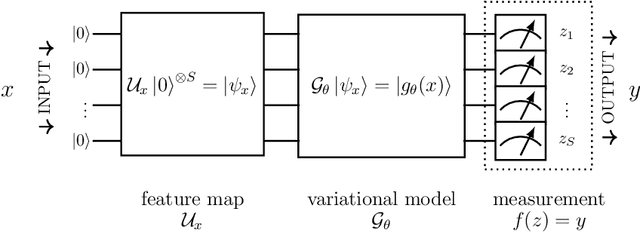
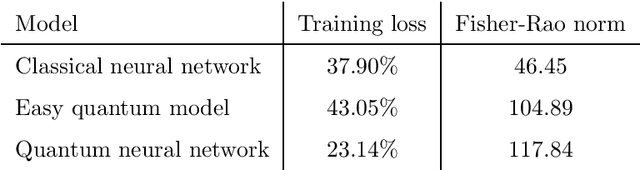
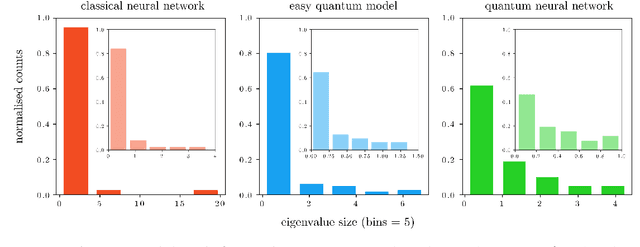
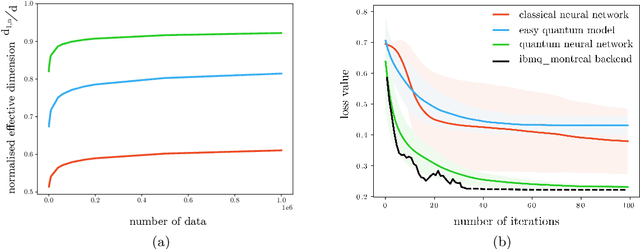
Fault-tolerant quantum computers offer the promise of dramatically improving machine learning through speed-ups in computation or improved model scalability. In the near-term, however, the benefits of quantum machine learning are not so clear. Understanding expressibility and trainability of quantum models-and quantum neural networks in particular-requires further investigation. In this work, we use tools from information geometry to define a notion of expressibility for quantum and classical models. The effective dimension, which depends on the Fisher information, is used to prove a novel generalisation bound and establish a robust measure of expressibility. We show that quantum neural networks are able to achieve a significantly better effective dimension than comparable classical neural networks. To then assess the trainability of quantum models, we connect the Fisher information spectrum to barren plateaus, the problem of vanishing gradients. Importantly, certain quantum neural networks can show resilience to this phenomenon and train faster than classical models due to their favourable optimisation landscapes, captured by a more evenly spread Fisher information spectrum. Our work is the first to demonstrate that well-designed quantum neural networks offer an advantage over classical neural networks through a higher effective dimension and faster training ability, which we verify on real quantum hardware.

PolyMapper: Extracting City Maps using Polygons

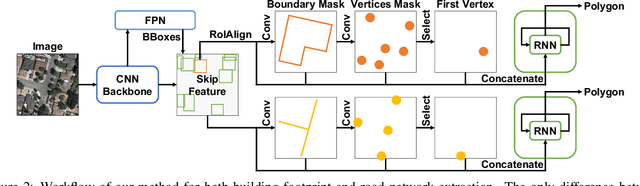
We propose a method to leapfrog pixel-wise, semantic segmentation of (aerial) images and predict objects in a vector representation directly. PolyMapper predicts maps of cities from aerial images as collections of polygons with a learnable framework. Instead of the usual multi-step procedure of semantic segmentation, shape improvement, conversion to polygons, and polygon refinement, our approach learns mappings with a single network architecture and directly outputs maps. We demonstrate that our method is capable of drawing polygons of buildings and road networks that very closely approximate the structure of existing online maps such as OpenStreetMap, and it does so in a fully automated manner. Validation on existing and novel large scale datasets of several cities show that our approach achieves good levels of performance.

Generator Reversal

We consider the problem of training generative models with deep neural networks as generators, i.e. to map latent codes to data points. Whereas the dominant paradigm combines simple priors over codes with complex deterministic models, we propose instead to use more flexible code distributions. These distributions are estimated non-parametrically by reversing the generator map during training. The benefits include: more powerful generative models, better modeling of latent structure and explicit control of the degree of generalization.