Marginalizable Density Models

Probability density models based on deep networks have achieved remarkable success in modeling complex high-dimensional datasets. However, unlike kernel density estimators, modern neural models do not yield marginals or conditionals in closed form, as these quantities require the evaluation of seldom tractable integrals. In this work, we present the Marginalizable Density Model Approximator (MDMA), a novel deep network architecture which provides closed form expressions for the probabilities, marginals and conditionals of any subset of the variables. The MDMA learns deep scalar representations for each individual variable and combines them via learned hierarchical tensor decompositions into a tractable yet expressive CDF, from which marginals and conditional densities are easily obtained. We illustrate the advantage of exact marginalizability in several tasks that are out of reach of previous deep network-based density estimation models, such as estimating mutual information between arbitrary subsets of variables, inferring causality by testing for conditional independence, and inference with missing data without the need for data imputation, outperforming state-of-the-art models on these tasks. The model also allows for parallelized sampling with only a logarithmic dependence of the time complexity on the number of variables.

Copulas as High-Dimensional Generative Models: Vine Copula Autoencoders

We propose a vine copula autoencoder to construct flexible generative models for high-dimensional distributions in a straightforward three-step procedure. First, an autoencoder compresses the data using a lower dimensional representation. Second, the multivariate distribution of the encoded data is estimated with vine copulas. Third, a generative model is obtained by combining the estimated distribution with the decoder part of the autoencoder. This approach can transform any already trained autoencoder into a flexible generative model at a low computational cost. This is an advantage over existing generative models such as adversarial networks and variational autoencoders which can be difficult to train and can impose strong assumptions on the latent space. Experiments on MNIST, Street View House Numbers and Large-Scale CelebFaces Attributes datasets show that vine copulas autoencoders can achieve competitive results to standard baselines.

Deep Smoothing of the Implied Volatility Surface

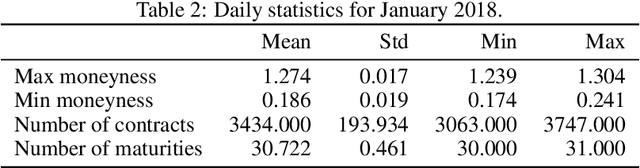
We present an artificial neural network (ANN) approach to value financial derivatives. Atypically to standard ANN applications, practitioners equally use option pricing models to validate market prices and to infer unobserved prices. Importantly, models need to generate realistic arbitrage-free prices, meaning that no option portfolio can lead to risk-free profits. The absence of arbitrage opportunities is guaranteed by penalizing the loss using soft constraints on an extended grid of input values. ANNs can be pre-trained by first calibrating a standard option pricing model, and then training an ANN to a larger synthetic dataset generated from the calibrated model. The parameters transfer as well as the non-arbitrage constraints appear to be particularly useful when only sparse or erroneous data are available. We also explore how deeper ANNs improve over shallower ones, as well as other properties of the network architecture. We benchmark our method against standard option pricing models, such as Heston with and without jumps. We validate our method both on training sets, and testing sets, namely, highlighting both their capacity to reproduce observed prices and predict new ones.

Generative Models for Simulating Mobility Trajectories

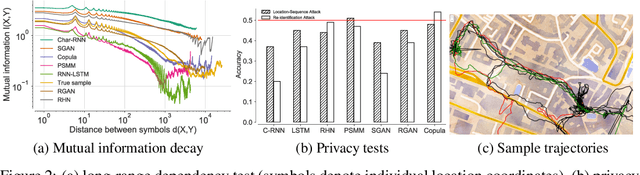
Mobility datasets are fundamental for evaluating algorithms pertaining to geographic information systems and facilitating experimental reproducibility. But privacy implications restrict sharing such datasets, as even aggregated location-data is vulnerable to membership inference attacks. Current synthetic mobility dataset generators attempt to superficially match a priori modeled mobility characteristics which do not accurately reflect the real-world characteristics. Modeling human mobility to generate synthetic yet semantically and statistically realistic trajectories is therefore crucial for publishing trajectory datasets having satisfactory utility level while preserving user privacy. Specifically, long-range dependencies inherent to human mobility are challenging to capture with both discriminative and generative models. In this paper, we benchmark the performance of recurrent neural architectures (RNNs), generative adversarial networks (GANs) and nonparametric copulas to generate synthetic mobility traces. We evaluate the generated trajectories with respect to their geographic and semantic similarity, circadian rhythms, long-range dependencies, training and generation time. We also include two sample tests to assess statistical similarity between the observed and simulated distributions, and we analyze the privacy tradeoffs with respect to membership inference and location-sequence attacks.

Nonparametric Quantile-Based Causal Discovery

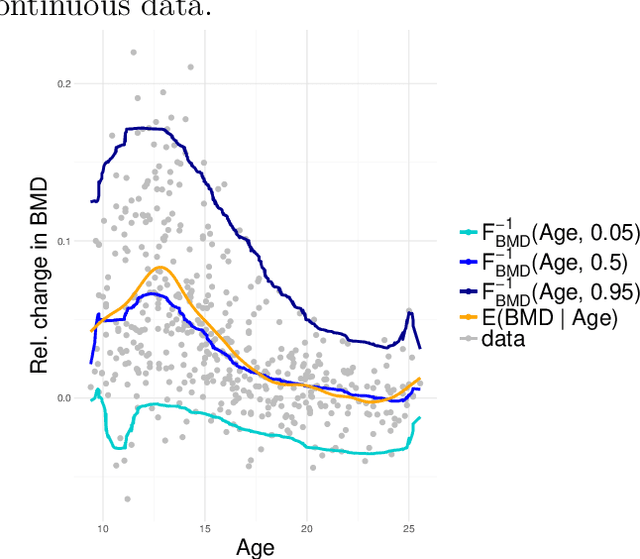
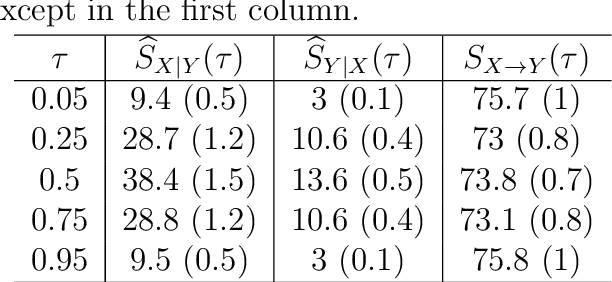
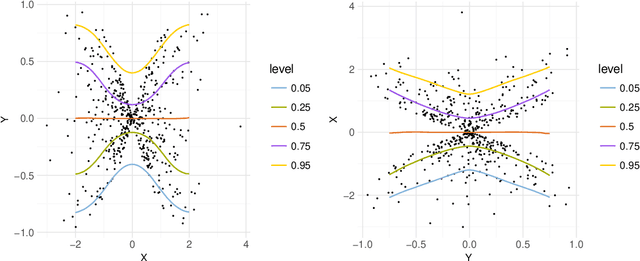
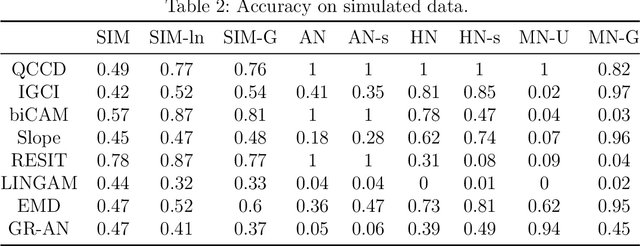
Distinguishing cause from effect using observational data is a challenging problem, especially in the bivariate case. Contemporary methods often assume an independence between the cause and the generating mechanism of the effect given the cause. From this postulate, they derive asymmetries to uncover causal relationships. Leveraging the same postulate, in this work, we propose a novel approach based on the link between Kolmogorov complexity and quantile scoring. We use a nonparametric conditional quantile estimator based on copulas to implement our procedure, thus avoiding restrictive assumptions about the joint distribution between cause and effect. In an extensive study on real and synthetic data, we show that quantile copula causal discovery (QCCD) compares favorably to state-of-the-art methods.