Copulas as High-Dimensional Generative Models: Vine Copula Autoencoders

We propose a vine copula autoencoder to construct flexible generative models for high-dimensional distributions in a straightforward three-step procedure. First, an autoencoder compresses the data using a lower dimensional representation. Second, the multivariate distribution of the encoded data is estimated with vine copulas. Third, a generative model is obtained by combining the estimated distribution with the decoder part of the autoencoder. This approach can transform any already trained autoencoder into a flexible generative model at a low computational cost. This is an advantage over existing generative models such as adversarial networks and variational autoencoders which can be difficult to train and can impose strong assumptions on the latent space. Experiments on MNIST, Street View House Numbers and Large-Scale CelebFaces Attributes datasets show that vine copulas autoencoders can achieve competitive results to standard baselines.

Deep Smoothing of the Implied Volatility Surface

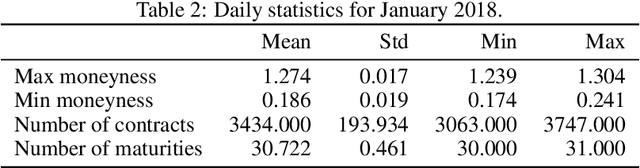
We present an artificial neural network (ANN) approach to value financial derivatives. Atypically to standard ANN applications, practitioners equally use option pricing models to validate market prices and to infer unobserved prices. Importantly, models need to generate realistic arbitrage-free prices, meaning that no option portfolio can lead to risk-free profits. The absence of arbitrage opportunities is guaranteed by penalizing the loss using soft constraints on an extended grid of input values. ANNs can be pre-trained by first calibrating a standard option pricing model, and then training an ANN to a larger synthetic dataset generated from the calibrated model. The parameters transfer as well as the non-arbitrage constraints appear to be particularly useful when only sparse or erroneous data are available. We also explore how deeper ANNs improve over shallower ones, as well as other properties of the network architecture. We benchmark our method against standard option pricing models, such as Heston with and without jumps. We validate our method both on training sets, and testing sets, namely, highlighting both their capacity to reproduce observed prices and predict new ones.