SEMF: Supervised Expectation-Maximization Framework for Predicting Intervals

This work introduces the Supervised Expectation-Maximization Framework (SEMF), a versatile and model-agnostic framework that generates prediction intervals for datasets with complete or missing data. SEMF extends the Expectation-Maximization (EM) algorithm, traditionally used in unsupervised learning, to a supervised context, enabling it to extract latent representations for uncertainty estimation. The framework demonstrates robustness through extensive empirical evaluation across 11 tabular datasets, achieving$\unicode{x2013}$in some cases$\unicode{x2013}$narrower normalized prediction intervals and higher coverage than traditional quantile regression methods. Furthermore, SEMF integrates seamlessly with existing machine learning algorithms, such as gradient-boosted trees and neural networks, exemplifying its usefulness for real-world applications. The experimental results highlight SEMF's potential to advance state-of-the-art techniques in uncertainty quantification.

Structural restrictions in local causal discovery: identifying direct causes of a target variable

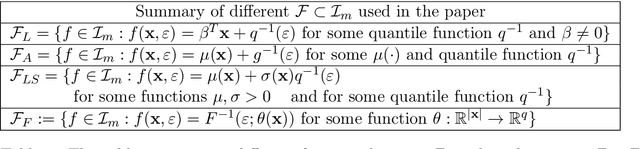
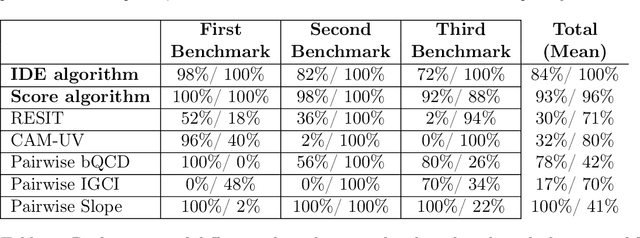
We consider the problem of learning a set of direct causes of a target variable from an observational joint distribution. Learning directed acyclic graphs (DAGs) that represent the causal structure is a fundamental problem in science. Several results are known when the full DAG is identifiable from the distribution, such as assuming a nonlinear Gaussian data-generating process. Often, we are only interested in identifying the direct causes of one target variable (local causal structure), not the full DAG. In this paper, we discuss different assumptions for the data-generating process of the target variable under which the set of direct causes is identifiable from the distribution. While doing so, we put essentially no assumptions on the variables other than the target variable. In addition to the novel identifiability results, we provide two practical algorithms for estimating the direct causes from a finite random sample and demonstrate their effectiveness on several benchmark datasets. We apply this framework to learn direct causes of the reduction in fertility rates in different countries.

Analyzing privacy-aware mobility behavior using the evolution of spatio-temporal entropy

Analyzing mobility behavior of users is extremely useful to create or improve existing services. Several research works have been done in order to study mobility behavior of users that mainly use users' significant locations. However, these existing analysis are extremely intrusive because they require the knowledge of the frequently visited places of users, which thus makes it fairly easy to identify them. Consequently, in this paper, we present a privacy-aware methodology to analyze mobility behavior of users. We firstly propose a new metric based on the well-known Shannon entropy, called spatio-temporal entropy, to quantify the mobility level of a user during a time window. Then, we compute a sequence of spatio-temporal entropy from the location history of the user that expresses user's movements as rhythms. We secondly present how to study the effects of several groups of additional variables on the evolution of the spatio-temporal entropy of a user, such as spatio-temporal, demographic and mean of transportation variables. For this, we use Generalized Additive Models (GAMs). The results firstly show that the spatio-temporal entropy and GAMs are an ideal combination to understand mobility behavior of an individual user or a group of users. We also evaluate the prediction accuracy of a global GAM compared to individual GAMs and individual AutoRegressive Integrated Moving Average (ARIMA) models. These last results highlighted that the global GAM gives more accurate predictions of spatio-temporal entropy by checking the Mean Absolute Error (MAE). In addition, this research work opens various threads, such as the prediction of demographic data of users or the creation of personalized mobility prediction models by using movement rhythm characteristics of a user.

Nonparametric Quantile-Based Causal Discovery

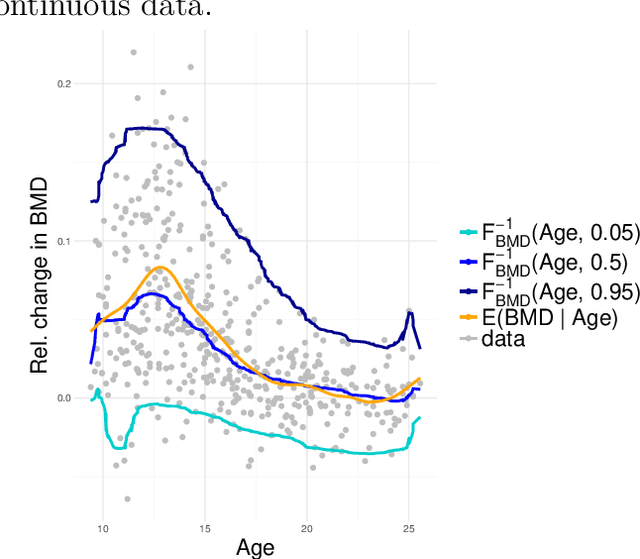
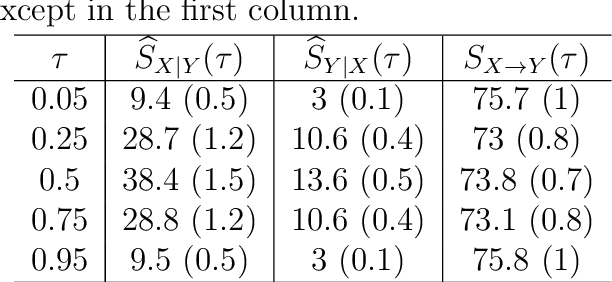
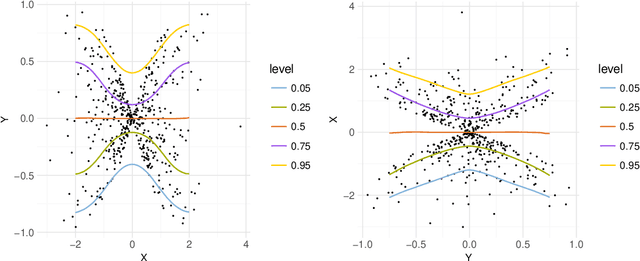
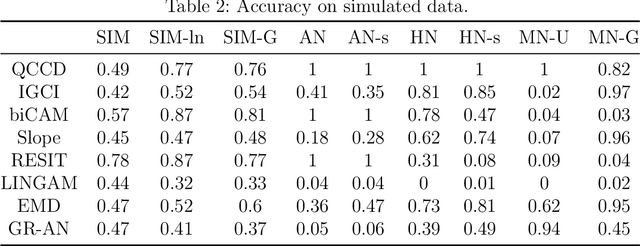
Distinguishing cause from effect using observational data is a challenging problem, especially in the bivariate case. Contemporary methods often assume an independence between the cause and the generating mechanism of the effect given the cause. From this postulate, they derive asymmetries to uncover causal relationships. Leveraging the same postulate, in this work, we propose a novel approach based on the link between Kolmogorov complexity and quantile scoring. We use a nonparametric conditional quantile estimator based on copulas to implement our procedure, thus avoiding restrictive assumptions about the joint distribution between cause and effect. In an extensive study on real and synthetic data, we show that quantile copula causal discovery (QCCD) compares favorably to state-of-the-art methods.