Granger Causality in Extremes

We introduce a rigorous mathematical framework for Granger causality in extremes, designed to identify causal links from extreme events in time series. Granger causality plays a pivotal role in uncovering directional relationships among time-varying variables. While this notion gains heightened importance during extreme and highly volatile periods, state-of-the-art methods primarily focus on causality within the body of the distribution, often overlooking causal mechanisms that manifest only during extreme events. Our framework is designed to infer causality mainly from extreme events by leveraging the causal tail coefficient. We establish equivalences between causality in extremes and other causal concepts, including (classical) Granger causality, Sims causality, and structural causality. We prove other key properties of Granger causality in extremes and show that the framework is especially helpful under the presence of hidden confounders. We also propose a novel inference method for detecting the presence of Granger causality in extremes from data. Our method is model-free, can handle non-linear and high-dimensional time series, outperforms current state-of-the-art methods in all considered setups, both in performance and speed, and was found to uncover coherent effects when applied to financial and extreme weather observations.

Structural restrictions in local causal discovery: identifying direct causes of a target variable

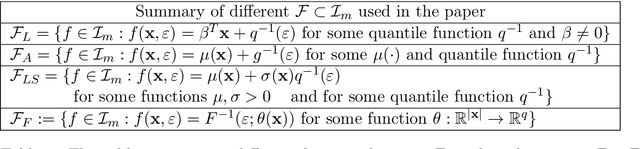
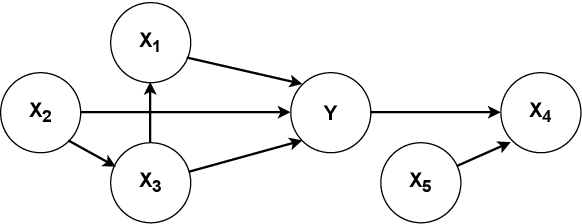
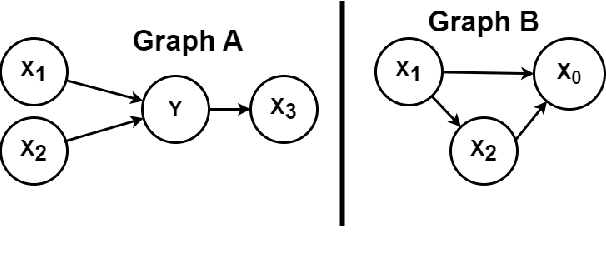
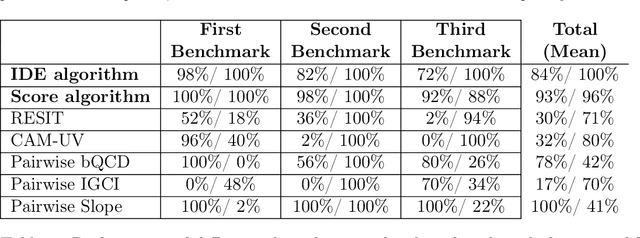
We consider the problem of learning a set of direct causes of a target variable from an observational joint distribution. Learning directed acyclic graphs (DAGs) that represent the causal structure is a fundamental problem in science. Several results are known when the full DAG is identifiable from the distribution, such as assuming a nonlinear Gaussian data-generating process. Often, we are only interested in identifying the direct causes of one target variable (local causal structure), not the full DAG. In this paper, we discuss different assumptions for the data-generating process of the target variable under which the set of direct causes is identifiable from the distribution. While doing so, we put essentially no assumptions on the variables other than the target variable. In addition to the novel identifiability results, we provide two practical algorithms for estimating the direct causes from a finite random sample and demonstrate their effectiveness on several benchmark datasets. We apply this framework to learn direct causes of the reduction in fertility rates in different countries.