Margalit Glasgow
Propagation of Chaos in One-hidden-layer Neural Networks beyond Logarithmic Time
Apr 17, 2025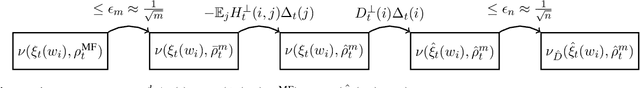

Abstract:We study the approximation gap between the dynamics of a polynomial-width neural network and its infinite-width counterpart, both trained using projected gradient descent in the mean-field scaling regime. We demonstrate how to tightly bound this approximation gap through a differential equation governed by the mean-field dynamics. A key factor influencing the growth of this ODE is the local Hessian of each particle, defined as the derivative of the particle's velocity in the mean-field dynamics with respect to its position. We apply our results to the canonical feature learning problem of estimating a well-specified single-index model; we permit the information exponent to be arbitrarily large, leading to convergence times that grow polynomially in the ambient dimension $d$. We show that, due to a certain ``self-concordance'' property in these problems -- where the local Hessian of a particle is bounded by a constant times the particle's velocity -- polynomially many neurons are sufficient to closely approximate the mean-field dynamics throughout training.
The Limits and Potentials of Local SGD for Distributed Heterogeneous Learning with Intermittent Communication
May 19, 2024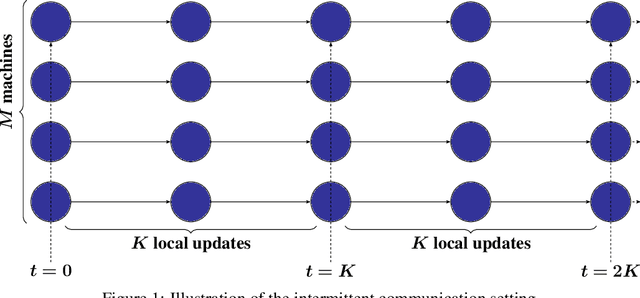

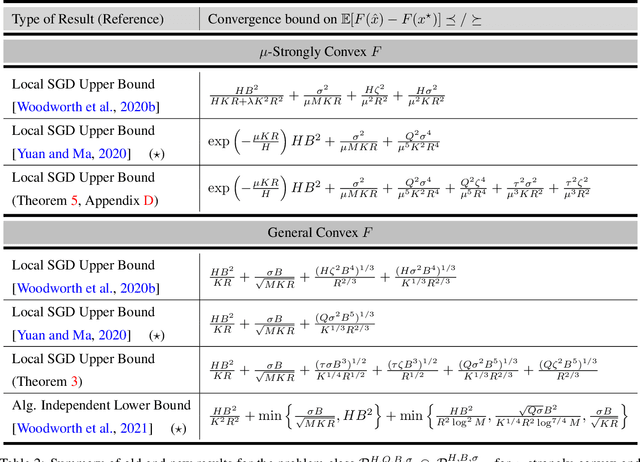
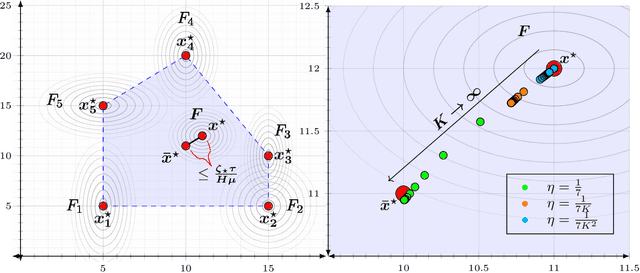
Abstract:Local SGD is a popular optimization method in distributed learning, often outperforming other algorithms in practice, including mini-batch SGD. Despite this success, theoretically proving the dominance of local SGD in settings with reasonable data heterogeneity has been difficult, creating a significant gap between theory and practice. In this paper, we provide new lower bounds for local SGD under existing first-order data heterogeneity assumptions, showing that these assumptions are insufficient to prove the effectiveness of local update steps. Furthermore, under these same assumptions, we demonstrate the min-max optimality of accelerated mini-batch SGD, which fully resolves our understanding of distributed optimization for several problem classes. Our results emphasize the need for better models of data heterogeneity to understand the effectiveness of local SGD in practice. Towards this end, we consider higher-order smoothness and heterogeneity assumptions, providing new upper bounds that imply the dominance of local SGD over mini-batch SGD when data heterogeneity is low.
SGD Finds then Tunes Features in Two-Layer Neural Networks with near-Optimal Sample Complexity: A Case Study in the XOR problem
Oct 02, 2023Abstract:In this work, we consider the optimization process of minibatch stochastic gradient descent (SGD) on a 2-layer neural network with data separated by a quadratic ground truth function. We prove that with data drawn from the $d$-dimensional Boolean hypercube labeled by the quadratic ``XOR'' function $y = -x_ix_j$, it is possible to train to a population error $o(1)$ with $d \:\text{polylog}(d)$ samples. Our result considers simultaneously training both layers of the two-layer-neural network with ReLU activations via standard minibatch SGD on the logistic loss. To our knowledge, this work is the first to give a sample complexity of $\tilde{O}(d)$ for efficiently learning the XOR function on isotropic data on a standard neural network with standard training. Our main technique is showing that the network evolves in two phases: a $\textit{signal-finding}$ phase where the network is small and many of the neurons evolve independently to find features, and a $\textit{signal-heavy}$ phase, where SGD maintains and balances the features. We leverage the simultaneous training of the layers to show that it is sufficient for only a small fraction of the neurons to learn features, since those neurons will be amplified by the simultaneous growth of their second layer weights.
Beyond NTK with Vanilla Gradient Descent: A Mean-Field Analysis of Neural Networks with Polynomial Width, Samples, and Time
Jun 28, 2023Abstract:Despite recent theoretical progress on the non-convex optimization of two-layer neural networks, it is still an open question whether gradient descent on neural networks without unnatural modifications can achieve better sample complexity than kernel methods. This paper provides a clean mean-field analysis of projected gradient flow on polynomial-width two-layer neural networks. Different from prior works, our analysis does not require unnatural modifications of the optimization algorithm. We prove that with sample size $n = O(d^{3.1})$ where $d$ is the dimension of the inputs, the network converges in polynomially many iterations to a non-trivial error that is not achievable by kernel methods using $n \ll d^4$ samples, hence demonstrating a clear separation between unmodified gradient descent and NTK.
Lower Bounds for $γ$-Regret via the Decision-Estimation Coefficient
Mar 06, 2023Abstract:In this note, we give a new lower bound for the $\gamma$-regret in bandit problems, the regret which arises when comparing against a benchmark that is $\gamma$ times the optimal solution, i.e., $\mathsf{Reg}_{\gamma}(T) = \sum_{t = 1}^T \gamma \max_{\pi} f(\pi) - f(\pi_t)$. The $\gamma$-regret arises in structured bandit problems where finding an exact optimum of $f$ is intractable. Our lower bound is given in terms of a modification of the constrained Decision-Estimation Coefficient (DEC) of~\citet{foster2023tight} (and closely related to the original offset DEC of \citet{foster2021statistical}), which we term the $\gamma$-DEC. When restricted to the traditional regret setting where $\gamma = 1$, our result removes the logarithmic factors in the lower bound of \citet{foster2023tight}.
Feature Dropout: Revisiting the Role of Augmentations in Contrastive Learning
Dec 16, 2022



Abstract:What role do augmentations play in contrastive learning? Recent work suggests that good augmentations are label-preserving with respect to a specific downstream task. We complicate this picture by showing that label-destroying augmentations can be useful in the foundation model setting, where the goal is to learn diverse, general-purpose representations for multiple downstream tasks. We perform contrastive learning experiments on a range of image and audio datasets with multiple downstream tasks (e.g. for digits superimposed on photographs, predicting the class of one vs. the other). We find that Viewmaker Networks, a recently proposed model for learning augmentations for contrastive learning, produce label-destroying augmentations that stochastically destroy features needed for different downstream tasks. These augmentations are interpretable (e.g. altering shapes, digits, or letters added to images) and surprisingly often result in better performance compared to expert-designed augmentations, despite not preserving label information. To support our empirical results, we theoretically analyze a simple contrastive learning setting with a linear model. In this setting, label-destroying augmentations are crucial for preventing one set of features from suppressing the learning of features useful for another downstream task. Our results highlight the need for analyzing the interaction between multiple downstream tasks when trying to explain the success of foundation models.
Max-Margin Works while Large Margin Fails: Generalization without Uniform Convergence
Jun 16, 2022
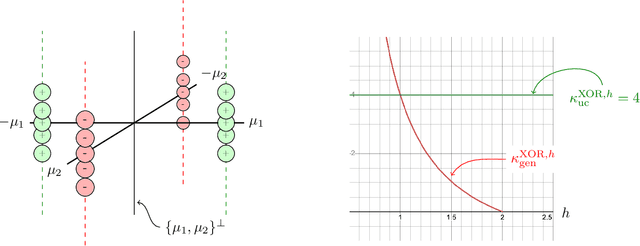
Abstract:A major challenge in modern machine learning is theoretically understanding the generalization properties of overparameterized models. Many existing tools rely on \em uniform convergence \em (UC), a property that, when it holds, guarantees that the test loss will be close to the training loss, uniformly over a class of candidate models. Nagarajan and Kolter (2019) show that in certain simple linear and neural-network settings, any uniform convergence bound will be vacuous, leaving open the question of how to prove generalization in settings where UC fails. Our main contribution is proving novel generalization bounds in two such settings, one linear, and one non-linear. We study the linear classification setting of Nagarajan and Kolter, and a quadratic ground truth function learned via a two-layer neural network in the non-linear regime. We prove a new type of margin bound showing that above a certain signal-to-noise threshold, any near-max-margin classifier will achieve almost no test loss in these two settings. Our results show that near-max-margin is important: while any model that achieves at least a $(1 - \epsilon)$-fraction of the max-margin generalizes well, a classifier achieving half of the max-margin may fail terribly. We additionally strengthen the UC impossibility results of Nagarajan and Kolter, proving that \em one-sided \em UC bounds and classical margin bounds will fail on near-max-margin classifiers. Our analysis provides insight on why memorization can coexist with generalization: we show that in this challenging regime where generalization occurs but UC fails, near-max-margin classifiers simultaneously contain some generalizable components and some overfitting components that memorize the data. The presence of the overfitting components is enough to preclude UC, but the near-extremal margin guarantees that sufficient generalizable components are present.
Sharp Bounds for Federated Averaging (Local SGD) and Continuous Perspective
Nov 05, 2021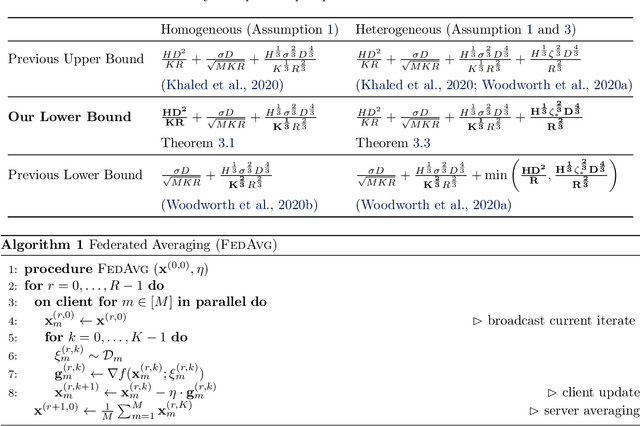
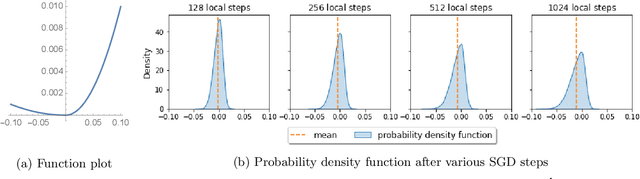
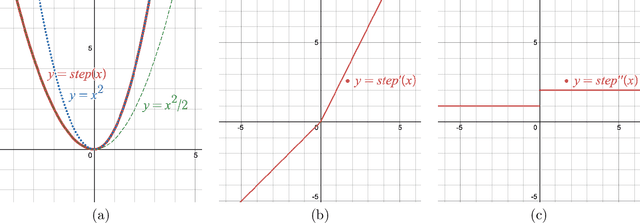
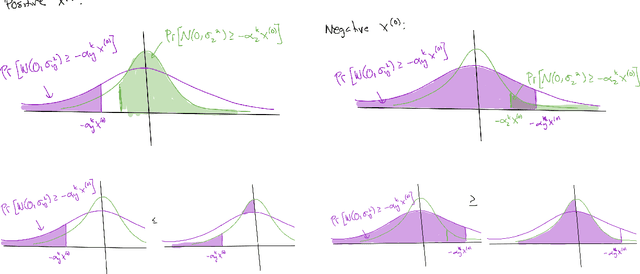
Abstract:Federated Averaging (FedAvg), also known as Local SGD, is one of the most popular algorithms in Federated Learning (FL). Despite its simplicity and popularity, the convergence rate of FedAvg has thus far been undetermined. Even under the simplest assumptions (convex, smooth, homogeneous, and bounded covariance), the best-known upper and lower bounds do not match, and it is not clear whether the existing analysis captures the capacity of the algorithm. In this work, we first resolve this question by providing a lower bound for FedAvg that matches the existing upper bound, which shows the existing FedAvg upper bound analysis is not improvable. Additionally, we establish a lower bound in a heterogeneous setting that nearly matches the existing upper bound. While our lower bounds show the limitations of FedAvg, under an additional assumption of third-order smoothness, we prove more optimistic state-of-the-art convergence results in both convex and non-convex settings. Our analysis stems from a notion we call iterate bias, which is defined by the deviation of the expectation of the SGD trajectory from the noiseless gradient descent trajectory with the same initialization. We prove novel sharp bounds on this quantity, and show intuitively how to analyze this quantity from a Stochastic Differential Equation (SDE) perspective.
Asynchronous Distributed Optimization with Randomized Delays
Oct 02, 2020


Abstract:In this work, we study asynchronous finite sum minimization in a distributed-data setting with a central parameter server. While asynchrony is well understood in parallel settings where the data is accessible by all machines, little is known for the distributed-data setting. We introduce a variant of SAGA called ADSAGA for the distributed-data setting where each machine stores a partition of the data. We show that with independent exponential work times -- a common assumption in distributed optimization -- ADSAGA converges in $\tilde{O}\left(\left(n + \sqrt{m}\kappa\right)\log(1/\epsilon)\right)$ iterations, where $n$ is the number of component functions, $m$ is the number of machines, and $\kappa$ is a condition number. We empirically compare the iteration complexity of ADSAGA to existing parallel and distributed algorithms, including synchronous mini-batch algorithms.
Approximate Gradient Coding with Optimal Decoding
Jun 17, 2020
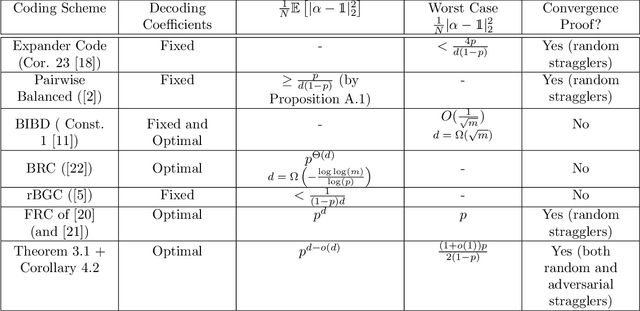

Abstract:In distributed optimization problems, a technique called gradient coding, which involves replicating data points, has been used to mitigate the effect of straggling machines. Recent work has studied approximate gradient coding, which concerns coding schemes where the replication factor of the data is too low to recover the full gradient exactly. Our work is motivated by the challenge of creating approximate gradient coding schemes that simultaneously work well in both the adversarial and stochastic models. To that end, we introduce novel approximate gradient codes based on expander graphs, in which each machine receives exactly two blocks of data points. We analyze the decoding error both in the random and adversarial straggler setting, when optimal decoding coefficients are used. We show that in the random setting, our schemes achieve an error to the gradient that decays exponentially in the replication factor. In the adversarial setting, the error is nearly a factor of two smaller than any existing code with similar performance in the random setting. We show convergence bounds both in the random and adversarial setting for gradient descent under standard assumptions using our codes. In the random setting, our convergence rate improves upon block-box bounds. In the adversarial setting, we show that gradient descent can converge down to a noise floor that scales linearly with the adversarial error to the gradient. We demonstrate empirically that our schemes achieve near-optimal error in the random setting and converge faster than algorithms which do not use the optimal decoding coefficients.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge