Sharp Bounds for Federated Averaging (Local SGD) and Continuous Perspective
Paper and Code
Nov 05, 2021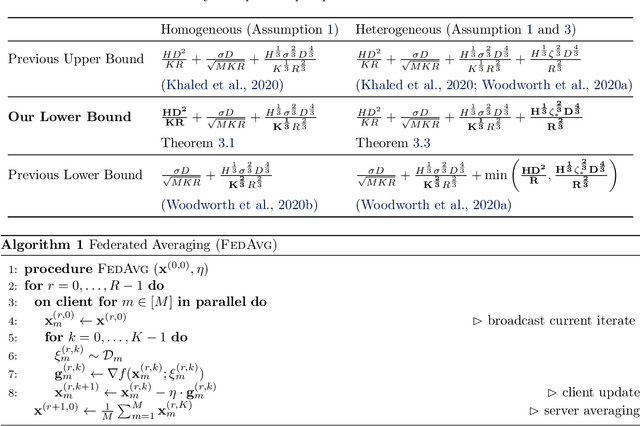
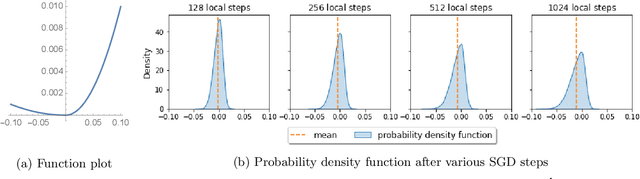
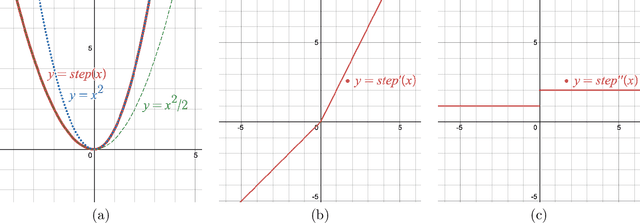
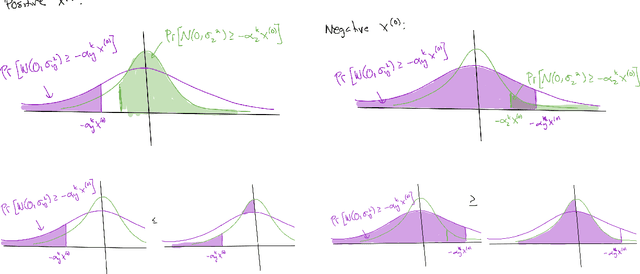
Federated Averaging (FedAvg), also known as Local SGD, is one of the most popular algorithms in Federated Learning (FL). Despite its simplicity and popularity, the convergence rate of FedAvg has thus far been undetermined. Even under the simplest assumptions (convex, smooth, homogeneous, and bounded covariance), the best-known upper and lower bounds do not match, and it is not clear whether the existing analysis captures the capacity of the algorithm. In this work, we first resolve this question by providing a lower bound for FedAvg that matches the existing upper bound, which shows the existing FedAvg upper bound analysis is not improvable. Additionally, we establish a lower bound in a heterogeneous setting that nearly matches the existing upper bound. While our lower bounds show the limitations of FedAvg, under an additional assumption of third-order smoothness, we prove more optimistic state-of-the-art convergence results in both convex and non-convex settings. Our analysis stems from a notion we call iterate bias, which is defined by the deviation of the expectation of the SGD trajectory from the noiseless gradient descent trajectory with the same initialization. We prove novel sharp bounds on this quantity, and show intuitively how to analyze this quantity from a Stochastic Differential Equation (SDE) perspective.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge