Honglin Yuan
On Principled Local Optimization Methods for Federated Learning
Jan 24, 2024Abstract:Federated Learning (FL), a distributed learning paradigm that scales on-device learning collaboratively, has emerged as a promising approach for decentralized AI applications. Local optimization methods such as Federated Averaging (FedAvg) are the most prominent methods for FL applications. Despite their simplicity and popularity, the theoretical understanding of local optimization methods is far from clear. This dissertation aims to advance the theoretical foundation of local methods in the following three directions. First, we establish sharp bounds for FedAvg, the most popular algorithm in Federated Learning. We demonstrate how FedAvg may suffer from a notion we call iterate bias, and how an additional third-order smoothness assumption may mitigate this effect and lead to better convergence rates. We explain this phenomenon from a Stochastic Differential Equation (SDE) perspective. Second, we propose Federated Accelerated Stochastic Gradient Descent (FedAc), the first principled acceleration of FedAvg, which provably improves the convergence rate and communication efficiency. Our technique uses on a potential-based perturbed iterate analysis, a novel stability analysis of generalized accelerated SGD, and a strategic tradeoff between acceleration and stability. Third, we study the Federated Composite Optimization problem, which extends the classic smooth setting by incorporating a shared non-smooth regularizer. We show that direct extensions of FedAvg may suffer from the "curse of primal averaging," resulting in slow convergence. As a solution, we propose a new primal-dual algorithm, Federated Dual Averaging, which overcomes the curse of primal averaging by employing a novel inter-client dual averaging procedure.
Plex: Towards Reliability using Pretrained Large Model Extensions
Jul 15, 2022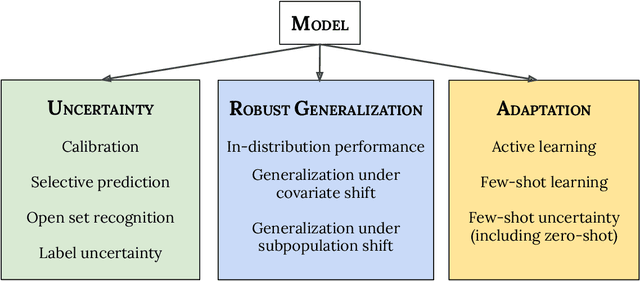

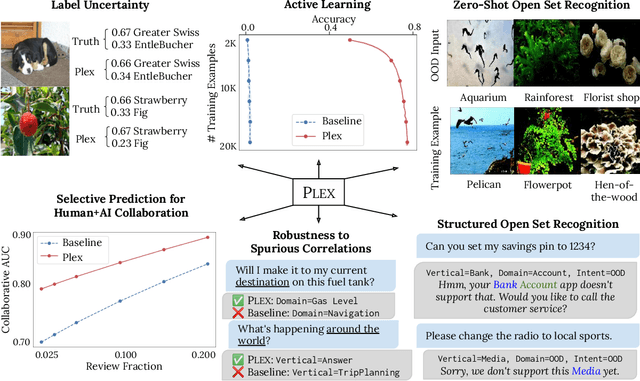

Abstract:A recent trend in artificial intelligence is the use of pretrained models for language and vision tasks, which have achieved extraordinary performance but also puzzling failures. Probing these models' abilities in diverse ways is therefore critical to the field. In this paper, we explore the reliability of models, where we define a reliable model as one that not only achieves strong predictive performance but also performs well consistently over many decision-making tasks involving uncertainty (e.g., selective prediction, open set recognition), robust generalization (e.g., accuracy and proper scoring rules such as log-likelihood on in- and out-of-distribution datasets), and adaptation (e.g., active learning, few-shot uncertainty). We devise 10 types of tasks over 40 datasets in order to evaluate different aspects of reliability on both vision and language domains. To improve reliability, we developed ViT-Plex and T5-Plex, pretrained large model extensions for vision and language modalities, respectively. Plex greatly improves the state-of-the-art across reliability tasks, and simplifies the traditional protocol as it improves the out-of-the-box performance and does not require designing scores or tuning the model for each task. We demonstrate scaling effects over model sizes up to 1B parameters and pretraining dataset sizes up to 4B examples. We also demonstrate Plex's capabilities on challenging tasks including zero-shot open set recognition, active learning, and uncertainty in conversational language understanding.
Sharp Bounds for Federated Averaging (Local SGD) and Continuous Perspective
Nov 05, 2021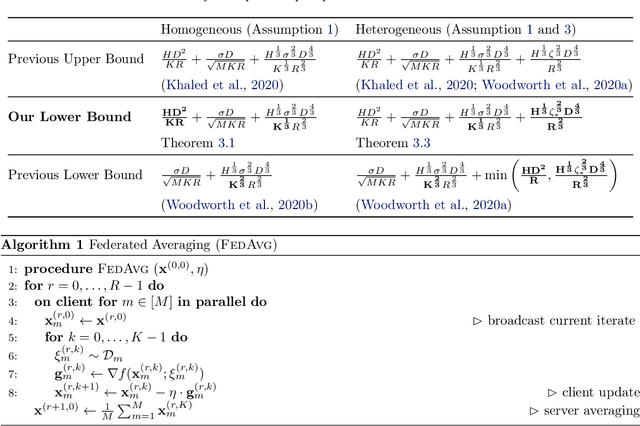
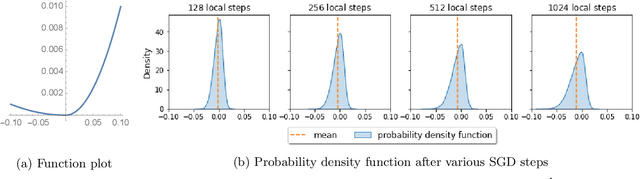
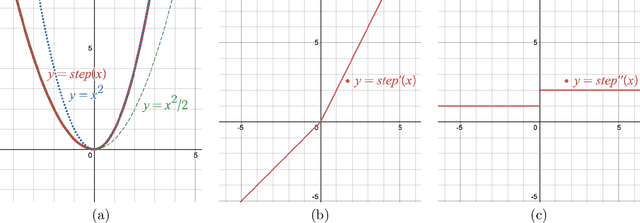
Abstract:Federated Averaging (FedAvg), also known as Local SGD, is one of the most popular algorithms in Federated Learning (FL). Despite its simplicity and popularity, the convergence rate of FedAvg has thus far been undetermined. Even under the simplest assumptions (convex, smooth, homogeneous, and bounded covariance), the best-known upper and lower bounds do not match, and it is not clear whether the existing analysis captures the capacity of the algorithm. In this work, we first resolve this question by providing a lower bound for FedAvg that matches the existing upper bound, which shows the existing FedAvg upper bound analysis is not improvable. Additionally, we establish a lower bound in a heterogeneous setting that nearly matches the existing upper bound. While our lower bounds show the limitations of FedAvg, under an additional assumption of third-order smoothness, we prove more optimistic state-of-the-art convergence results in both convex and non-convex settings. Our analysis stems from a notion we call iterate bias, which is defined by the deviation of the expectation of the SGD trajectory from the noiseless gradient descent trajectory with the same initialization. We prove novel sharp bounds on this quantity, and show intuitively how to analyze this quantity from a Stochastic Differential Equation (SDE) perspective.
Big-Step-Little-Step: Efficient Gradient Methods for Objectives with Multiple Scales
Nov 04, 2021

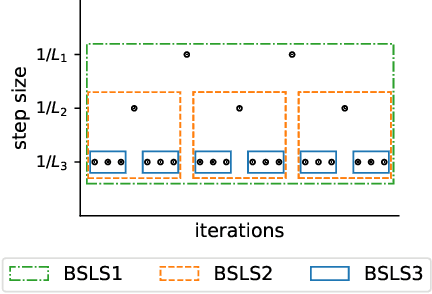

Abstract:We provide new gradient-based methods for efficiently solving a broad class of ill-conditioned optimization problems. We consider the problem of minimizing a function $f : \mathbb{R}^d \rightarrow \mathbb{R}$ which is implicitly decomposable as the sum of $m$ unknown non-interacting smooth, strongly convex functions and provide a method which solves this problem with a number of gradient evaluations that scales (up to logarithmic factors) as the product of the square-root of the condition numbers of the components. This complexity bound (which we prove is nearly optimal) can improve almost exponentially on that of accelerated gradient methods, which grow as the square root of the condition number of $f$. Additionally, we provide efficient methods for solving stochastic, quadratic variants of this multiscale optimization problem. Rather than learn the decomposition of $f$ (which would be prohibitively expensive), our methods apply a clean recursive "Big-Step-Little-Step" interleaving of standard methods. The resulting algorithms use $\tilde{\mathcal{O}}(d m)$ space, are numerically stable, and open the door to a more fine-grained understanding of the complexity of convex optimization beyond condition number.
What Do We Mean by Generalization in Federated Learning?
Oct 27, 2021
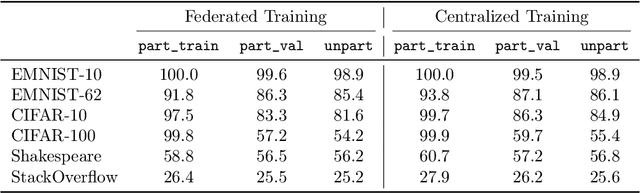
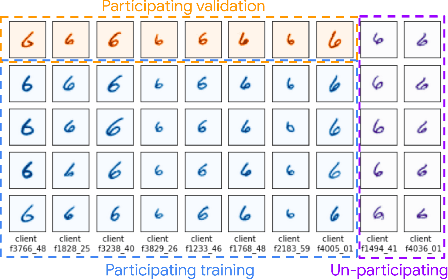
Abstract:Federated learning data is drawn from a distribution of distributions: clients are drawn from a meta-distribution, and their data are drawn from local data distributions. Thus generalization studies in federated learning should separate performance gaps from unseen client data (out-of-sample gap) from performance gaps from unseen client distributions (participation gap). In this work, we propose a framework for disentangling these performance gaps. Using this framework, we observe and explain differences in behavior across natural and synthetic federated datasets, indicating that dataset synthesis strategy can be important for realistic simulations of generalization in federated learning. We propose a semantic synthesis strategy that enables realistic simulation without naturally-partitioned data. Informed by our findings, we call out community suggestions for future federated learning works.
A Field Guide to Federated Optimization
Jul 14, 2021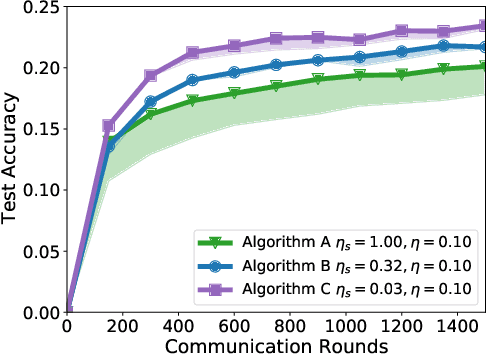


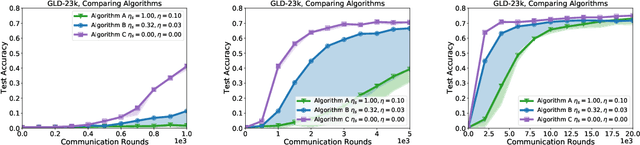
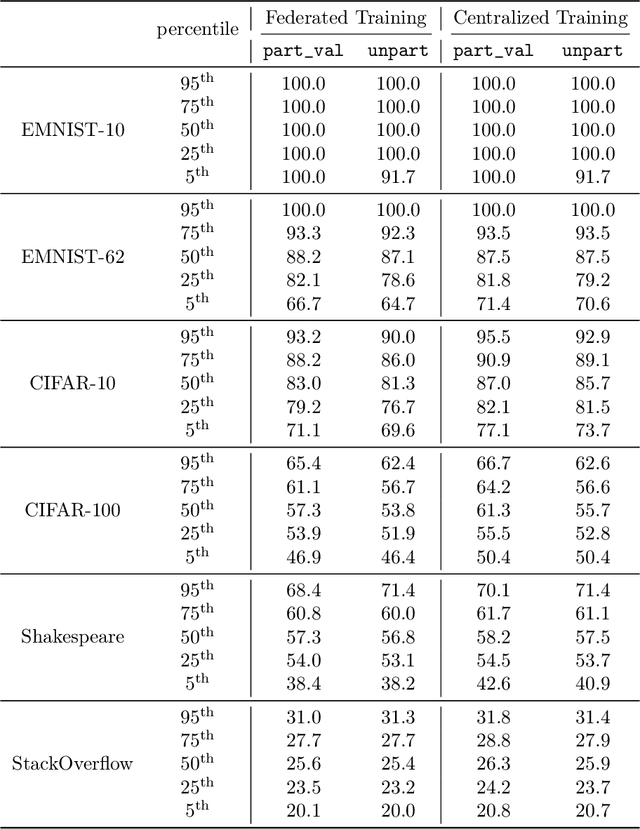
Abstract:Federated learning and analytics are a distributed approach for collaboratively learning models (or statistics) from decentralized data, motivated by and designed for privacy protection. The distributed learning process can be formulated as solving federated optimization problems, which emphasize communication efficiency, data heterogeneity, compatibility with privacy and system requirements, and other constraints that are not primary considerations in other problem settings. This paper provides recommendations and guidelines on formulating, designing, evaluating and analyzing federated optimization algorithms through concrete examples and practical implementation, with a focus on conducting effective simulations to infer real-world performance. The goal of this work is not to survey the current literature, but to inspire researchers and practitioners to design federated learning algorithms that can be used in various practical applications.
Federated Composite Optimization
Nov 17, 2020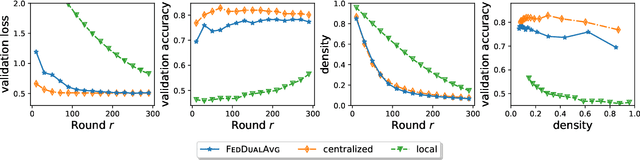

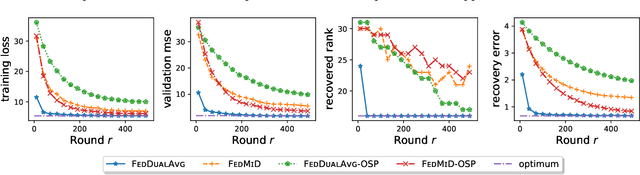
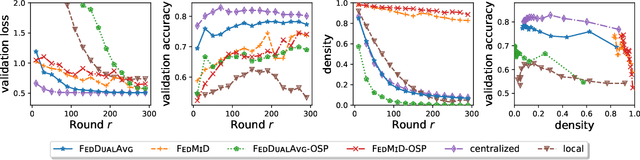
Abstract:Federated Learning (FL) is a distributed learning paradigm which scales on-device learning collaboratively and privately. Standard FL algorithms such as Federated Averaging (FedAvg) are primarily geared towards smooth unconstrained settings. In this paper, we study the Federated Composite Optimization (FCO) problem, where the objective function in FL includes an additive (possibly) non-smooth component. Such optimization problems are fundamental to machine learning and arise naturally in the context of regularization (e.g., sparsity, low-rank, monotonicity, and constraint). To tackle this problem, we propose different primal/dual averaging approaches and study their communication and computation complexities. Of particular interest is Federated Dual Averaging (FedDualAvg), a federated variant of the dual averaging algorithm. FedDualAvg uses a novel double averaging procedure, which involves gradient averaging step in standard dual averaging and an average of client updates akin to standard federated averaging. Our theoretical analysis and empirical experiments demonstrate that FedDualAvg outperforms baselines for FCO.
SHREC 2020 track: 6D Object Pose Estimation
Oct 19, 2020
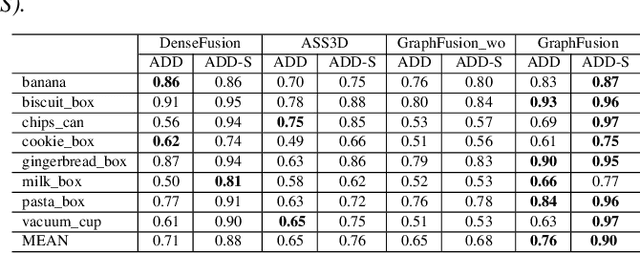
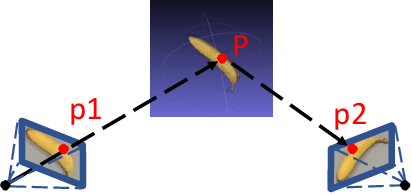
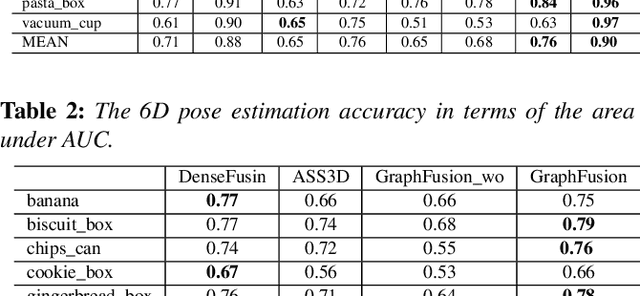
Abstract:6D pose estimation is crucial for augmented reality, virtual reality, robotic manipulation and visual navigation. However, the problem is challenging due to the variety of objects in the real world. They have varying 3D shape and their appearances in captured images are affected by sensor noise, changing lighting conditions and occlusions between objects. Different pose estimation methods have different strengths and weaknesses, depending on feature representations and scene contents. At the same time, existing 3D datasets that are used for data-driven methods to estimate 6D poses have limited view angles and low resolution. To address these issues, we organize the Shape Retrieval Challenge benchmark on 6D pose estimation and create a physically accurate simulator that is able to generate photo-realistic color-and-depth image pairs with corresponding ground truth 6D poses. From captured color and depth images, we use this simulator to generate a 3D dataset which has 400 photo-realistic synthesized color-and-depth image pairs with various view angles for training, and another 100 captured and synthetic images for testing. Five research groups register in this track and two of them submitted their results. Data-driven methods are the current trend in 6D object pose estimation and our evaluation results show that approaches which fully exploit the color and geometric features are more robust for 6D pose estimation of reflective and texture-less objects and occlusion. This benchmark and comparative evaluation results have the potential to further enrich and boost the research of 6D object pose estimation and its applications.
Federated Accelerated Stochastic Gradient Descent
Jun 19, 2020



Abstract:We propose Federated Accelerated Stochastic Gradient Descent (FedAc), a principled acceleration of Federated Averaging (FedAvg, also known as Local SGD) for distributed optimization. FedAc is the first provable acceleration of FedAvg that improves convergence speed and communication efficiency on various types of convex functions. For example, for strongly convex and smooth functions, when using $M$ workers, the previous state-of-the-art FedAvg analysis can achieve a linear speedup in $M$ if given $M$ rounds of synchronization, whereas FedAc only requires $M^{\frac{1}{3}}$ rounds. Moreover, we prove stronger guarantees for FedAc when the objectives are third-order smooth. Our technique is based on a potential-based perturbed iterate analysis, a novel stability analysis of generalized accelerated SGD, and a strategic tradeoff between acceleration and stability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge