Learning Mixtures of Gaussians Using Diffusion Models

We give a new algorithm for learning mixtures of $k$ Gaussians (with identity covariance in $\mathbb{R}^n$) to TV error $\varepsilon$, with quasi-polynomial ($O(n^{\text{poly log}\left(\frac{n+k}{\varepsilon}\right)})$) time and sample complexity, under a minimum weight assumption. Unlike previous approaches, most of which are algebraic in nature, our approach is analytic and relies on the framework of diffusion models. Diffusion models are a modern paradigm for generative modeling, which typically rely on learning the score function (gradient log-pdf) along a process transforming a pure noise distribution, in our case a Gaussian, to the data distribution. Despite their dazzling performance in tasks such as image generation, there are few end-to-end theoretical guarantees that they can efficiently learn nontrivial families of distributions; we give some of the first such guarantees. We proceed by deriving higher-order Gaussian noise sensitivity bounds for the score functions for a Gaussian mixture to show that that they can be inductively learned using piecewise polynomial regression (up to poly-logarithmic degree), and combine this with known convergence results for diffusion models. Our results extend to continuous mixtures of Gaussians where the mixing distribution is supported on a union of $k$ balls of constant radius. In particular, this applies to the case of Gaussian convolutions of distributions on low-dimensional manifolds, or more generally sets with small covering number.

Lasso with Latents: Efficient Estimation, Covariate Rescaling, and Computational-Statistical Gaps

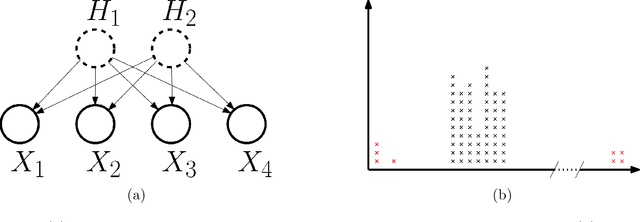
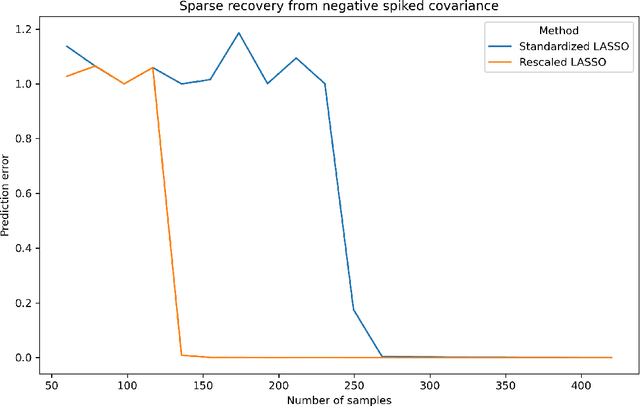
It is well-known that the statistical performance of Lasso can suffer significantly when the covariates of interest have strong correlations. In particular, the prediction error of Lasso becomes much worse than computationally inefficient alternatives like Best Subset Selection. Due to a large conjectured computational-statistical tradeoff in the problem of sparse linear regression, it may be impossible to close this gap in general. In this work, we propose a natural sparse linear regression setting where strong correlations between covariates arise from unobserved latent variables. In this setting, we analyze the problem caused by strong correlations and design a surprisingly simple fix. While Lasso with standard normalization of covariates fails, there exists a heterogeneous scaling of the covariates with which Lasso will suddenly obtain strong provable guarantees for estimation. Moreover, we design a simple, efficient procedure for computing such a "smart scaling." The sample complexity of the resulting "rescaled Lasso" algorithm incurs (in the worst case) quadratic dependence on the sparsity of the underlying signal. While this dependence is not information-theoretically necessary, we give evidence that it is optimal among the class of polynomial-time algorithms, via the method of low-degree polynomials. This argument reveals a new connection between sparse linear regression and a special version of sparse PCA with a near-critical negative spike. The latter problem can be thought of as a real-valued analogue of learning a sparse parity. Using it, we also establish the first computational-statistical gap for the closely related problem of learning a Gaussian Graphical Model.

Feature Adaptation for Sparse Linear Regression

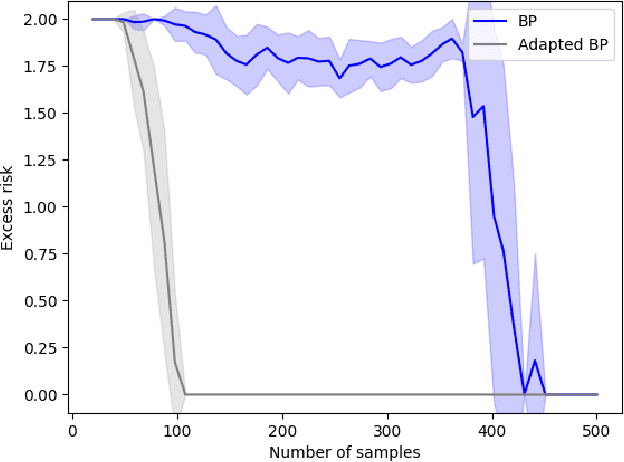
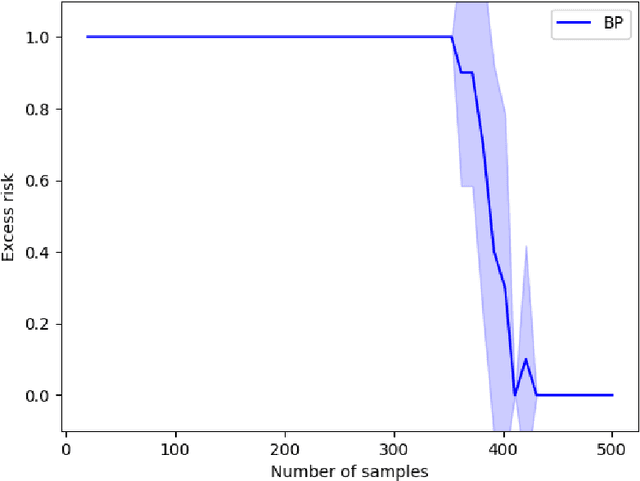
Sparse linear regression is a central problem in high-dimensional statistics. We study the correlated random design setting, where the covariates are drawn from a multivariate Gaussian $N(0,\Sigma)$, and we seek an estimator with small excess risk. If the true signal is $t$-sparse, information-theoretically, it is possible to achieve strong recovery guarantees with only $O(t\log n)$ samples. However, computationally efficient algorithms have sample complexity linear in (some variant of) the condition number of $\Sigma$. Classical algorithms such as the Lasso can require significantly more samples than necessary even if there is only a single sparse approximate dependency among the covariates. We provide a polynomial-time algorithm that, given $\Sigma$, automatically adapts the Lasso to tolerate a small number of approximate dependencies. In particular, we achieve near-optimal sample complexity for constant sparsity and if $\Sigma$ has few ``outlier'' eigenvalues. Our algorithm fits into a broader framework of feature adaptation for sparse linear regression with ill-conditioned covariates. With this framework, we additionally provide the first polynomial-factor improvement over brute-force search for constant sparsity $t$ and arbitrary covariance $\Sigma$.

Sampling with Barriers: Faster Mixing via Lewis Weights

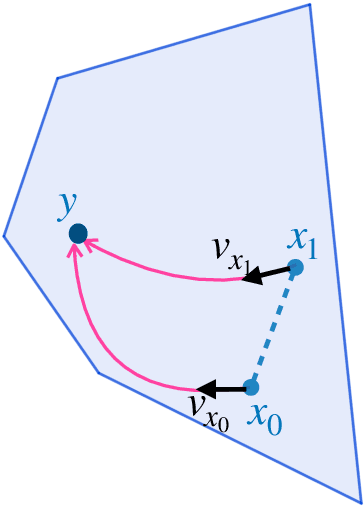
We analyze Riemannian Hamiltonian Monte Carlo (RHMC) for sampling a polytope defined by $m$ inequalities in $\R^n$ endowed with the metric defined by the Hessian of a self-concordant convex barrier function. We use a hybrid of the $p$-Lewis weight barrier and the standard logarithmic barrier and prove that the mixing rate is bounded by $\tilde O(m^{1/3}n^{4/3})$, improving on the previous best bound of $\tilde O(mn^{2/3})$, based on the log barrier. Our analysis overcomes several technical challenges to establish this result, in the process deriving smoothness bounds on Hamiltonian curves and extending self-concordance notions to the infinity norm; both properties appear to be of independent interest.

Big-Step-Little-Step: Efficient Gradient Methods for Objectives with Multiple Scales

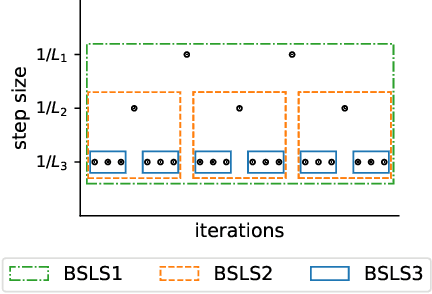
We provide new gradient-based methods for efficiently solving a broad class of ill-conditioned optimization problems. We consider the problem of minimizing a function $f : \mathbb{R}^d \rightarrow \mathbb{R}$ which is implicitly decomposable as the sum of $m$ unknown non-interacting smooth, strongly convex functions and provide a method which solves this problem with a number of gradient evaluations that scales (up to logarithmic factors) as the product of the square-root of the condition numbers of the components. This complexity bound (which we prove is nearly optimal) can improve almost exponentially on that of accelerated gradient methods, which grow as the square root of the condition number of $f$. Additionally, we provide efficient methods for solving stochastic, quadratic variants of this multiscale optimization problem. Rather than learn the decomposition of $f$ (which would be prohibitively expensive), our methods apply a clean recursive "Big-Step-Little-Step" interleaving of standard methods. The resulting algorithms use $\tilde{\mathcal{O}}(d m)$ space, are numerically stable, and open the door to a more fine-grained understanding of the complexity of convex optimization beyond condition number.

On the Power of Preconditioning in Sparse Linear Regression

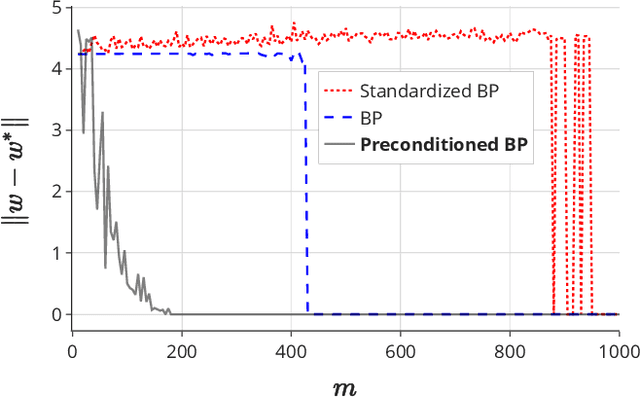
Sparse linear regression is a fundamental problem in high-dimensional statistics, but strikingly little is known about how to efficiently solve it without restrictive conditions on the design matrix. We consider the (correlated) random design setting, where the covariates are independently drawn from a multivariate Gaussian $N(0,\Sigma)$ with $\Sigma : n \times n$, and seek estimators $\hat{w}$ minimizing $(\hat{w}-w^*)^T\Sigma(\hat{w}-w^*)$, where $w^*$ is the $k$-sparse ground truth. Information theoretically, one can achieve strong error bounds with $O(k \log n)$ samples for arbitrary $\Sigma$ and $w^*$; however, no efficient algorithms are known to match these guarantees even with $o(n)$ samples, without further assumptions on $\Sigma$ or $w^*$. As far as hardness, computational lower bounds are only known with worst-case design matrices. Random-design instances are known which are hard for the Lasso, but these instances can generally be solved by Lasso after a simple change-of-basis (i.e. preconditioning). In this work, we give upper and lower bounds clarifying the power of preconditioning in sparse linear regression. First, we show that the preconditioned Lasso can solve a large class of sparse linear regression problems nearly optimally: it succeeds whenever the dependency structure of the covariates, in the sense of the Markov property, has low treewidth -- even if $\Sigma$ is highly ill-conditioned. Second, we construct (for the first time) random-design instances which are provably hard for an optimally preconditioned Lasso. In fact, we complete our treewidth classification by proving that for any treewidth-$t$ graph, there exists a Gaussian Markov Random Field on this graph such that the preconditioned Lasso, with any choice of preconditioner, requires $\Omega(t^{1/20})$ samples to recover $O(\log n)$-sparse signals when covariates are drawn from this model.

Learning Some Popular Gaussian Graphical Models without Condition Number Bounds

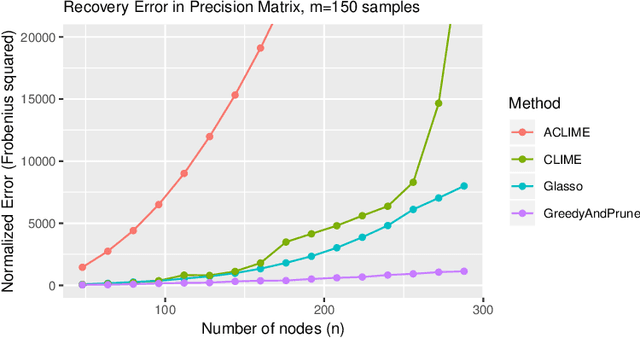
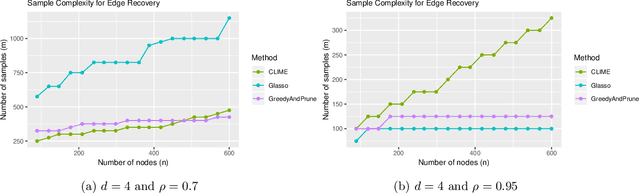
Gaussian Graphical Models (GGMs) have wide-ranging applications in machine learning and the natural and social sciences. In most of the settings in which they are applied, the number of observed samples is much smaller than the dimension and they are assumed to be sparse. While there are a variety of algorithms (e.g. Graphical Lasso, CLIME) that provably recover the graph structure with a logarithmic number of samples, they assume various conditions that require the precision matrix to be in some sense well-conditioned. Here we give the first polynomial-time algorithms for learning attractive GGMs and walk-summable GGMs with a logarithmic number of samples without any such assumptions. In particular, our algorithms can tolerate strong dependencies among the variables. We complement our results with experiments showing that many existing algorithms fail even in some simple settings where there are long dependency chains, whereas ours do not.

Rounding Sum-of-Squares Relaxations

We present a general approach to rounding semidefinite programming relaxations obtained by the Sum-of-Squares method (Lasserre hierarchy). Our approach is based on using the connection between these relaxations and the Sum-of-Squares proof system to transform a *combining algorithm* -- an algorithm that maps a distribution over solutions into a (possibly weaker) solution -- into a *rounding algorithm* that maps a solution of the relaxation to a solution of the original problem. Using this approach, we obtain algorithms that yield improved results for natural variants of three well-known problems: 1) We give a quasipolynomial-time algorithm that approximates the maximum of a low degree multivariate polynomial with non-negative coefficients over the Euclidean unit sphere. Beyond being of interest in its own right, this is related to an open question in quantum information theory, and our techniques have already led to improved results in this area (Brand\~{a}o and Harrow, STOC '13). 2) We give a polynomial-time algorithm that, given a d dimensional subspace of R^n that (almost) contains the characteristic function of a set of size n/k, finds a vector $v$ in the subspace satisfying $|v|_4^4 > c(k/d^{1/3}) |v|_2^2$, where $|v|_p = (E_i v_i^p)^{1/p}$. Aside from being a natural relaxation, this is also motivated by a connection to the Small Set Expansion problem shown by Barak et al. (STOC 2012) and our results yield a certain improvement for that problem. 3) We use this notion of L_4 vs. L_2 sparsity to obtain a polynomial-time algorithm with substantially improved guarantees for recovering a planted $\mu$-sparse vector v in a random d-dimensional subspace of R^n. If v has mu n nonzero coordinates, we can recover it with high probability whenever $\mu < O(\min(1,n/d^2))$, improving for $d < n^{2/3}$ prior methods which intrinsically required $\mu < O(1/\sqrt(d))$.