Fast Mixing of Data Augmentation Algorithms: Bayesian Probit, Logit, and Lasso Regression

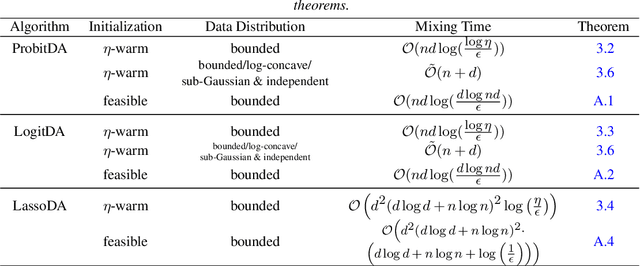
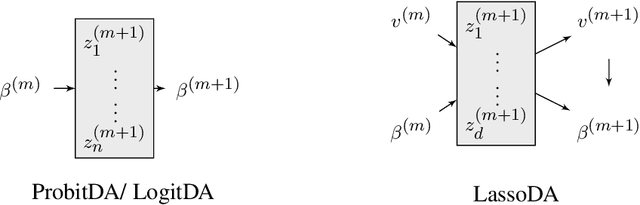
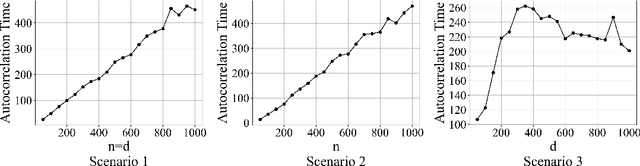
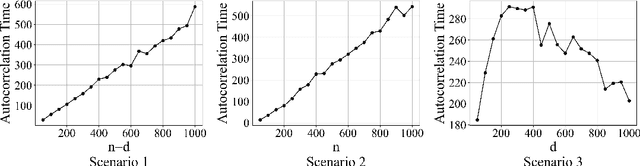
Despite the widespread use of the data augmentation (DA) algorithm, the theoretical understanding of its convergence behavior remains incomplete. We prove the first non-asymptotic polynomial upper bounds on mixing times of three important DA algorithms: DA algorithm for Bayesian Probit regression (Albert and Chib, 1993, ProbitDA), Bayesian Logit regression (Polson, Scott, and Windle, 2013, LogitDA), and Bayesian Lasso regression (Park and Casella, 2008, Rajaratnam et al., 2015, LassoDA). Concretely, we demonstrate that with $\eta$-warm start, parameter dimension $d$, and sample size $n$, the ProbitDA and LogitDA require $\mathcal{O}\left(nd\log \left(\frac{\log \eta}{\epsilon}\right)\right)$ steps to obtain samples with at most $\epsilon$ TV error, whereas the LassoDA requires $\mathcal{O}\left(d^2(d\log d +n \log n)^2 \log \left(\frac{\eta}{\epsilon}\right)\right)$ steps. The results are generally applicable to settings with large $n$ and large $d$, including settings with highly imbalanced response data in the Probit and Logit regression. The proofs are based on the Markov chain conductance and isoperimetric inequalities. Assuming that data are independently generated from either a bounded, sub-Gaussian, or log-concave distribution, we improve the guarantees for ProbitDA and LogitDA to $\tilde{\mathcal{O}}(n+d)$ with high probability, and compare it with the best known guarantees of Langevin Monte Carlo and Metropolis Adjusted Langevin Algorithm. We also discuss the mixing times of the three algorithms under feasible initialization.

Efficiently learning and sampling multimodal distributions with data-based initialization

We consider the problem of sampling a multimodal distribution with a Markov chain given a small number of samples from the stationary measure. Although mixing can be arbitrarily slow, we show that if the Markov chain has a $k$th order spectral gap, initialization from a set of $\tilde O(k/\varepsilon^2)$ samples from the stationary distribution will, with high probability over the samples, efficiently generate a sample whose conditional law is $\varepsilon$-close in TV distance to the stationary measure. In particular, this applies to mixtures of $k$ distributions satisfying a Poincar\'e inequality, with faster convergence when they satisfy a log-Sobolev inequality. Our bounds are stable to perturbations to the Markov chain, and in particular work for Langevin diffusion over $\mathbb R^d$ with score estimation error, as well as Glauber dynamics combined with approximation error from pseudolikelihood estimation. This justifies the success of data-based initialization for score matching methods despite slow mixing for the data distribution, and improves and generalizes the results of Koehler and Vuong (2023) to have linear, rather than exponential, dependence on $k$ and apply to arbitrary semigroups. As a consequence of our results, we show for the first time that a natural class of low-complexity Ising measures can be efficiently learned from samples.

Convergence Bounds for Sequential Monte Carlo on Multimodal Distributions using Soft Decomposition

We prove bounds on the variance of a function $f$ under the empirical measure of the samples obtained by the Sequential Monte Carlo (SMC) algorithm, with time complexity depending on local rather than global Markov chain mixing dynamics. SMC is a Markov Chain Monte Carlo (MCMC) method, which starts by drawing $N$ particles from a known distribution, and then, through a sequence of distributions, re-weights and re-samples the particles, at each instance applying a Markov chain for smoothing. In principle, SMC tries to alleviate problems from multi-modality. However, most theoretical guarantees for SMC are obtained by assuming global mixing time bounds, which are only efficient in the uni-modal setting. We show that bounds can be obtained in the truly multi-modal setting, with mixing times that depend only on local MCMC dynamics.

Learning Mixtures of Gaussians Using Diffusion Models

We give a new algorithm for learning mixtures of $k$ Gaussians (with identity covariance in $\mathbb{R}^n$) to TV error $\varepsilon$, with quasi-polynomial ($O(n^{\text{poly log}\left(\frac{n+k}{\varepsilon}\right)})$) time and sample complexity, under a minimum weight assumption. Unlike previous approaches, most of which are algebraic in nature, our approach is analytic and relies on the framework of diffusion models. Diffusion models are a modern paradigm for generative modeling, which typically rely on learning the score function (gradient log-pdf) along a process transforming a pure noise distribution, in our case a Gaussian, to the data distribution. Despite their dazzling performance in tasks such as image generation, there are few end-to-end theoretical guarantees that they can efficiently learn nontrivial families of distributions; we give some of the first such guarantees. We proceed by deriving higher-order Gaussian noise sensitivity bounds for the score functions for a Gaussian mixture to show that that they can be inductively learned using piecewise polynomial regression (up to poly-logarithmic degree), and combine this with known convergence results for diffusion models. Our results extend to continuous mixtures of Gaussians where the mixing distribution is supported on a union of $k$ balls of constant radius. In particular, this applies to the case of Gaussian convolutions of distributions on low-dimensional manifolds, or more generally sets with small covering number.

How Flawed is ECE? An Analysis via Logit Smoothing

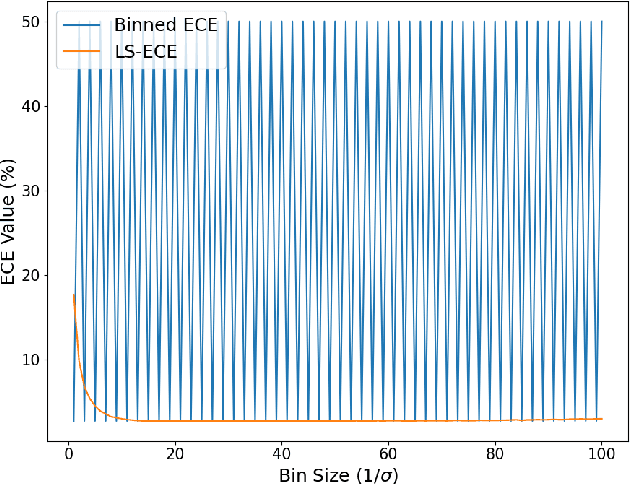
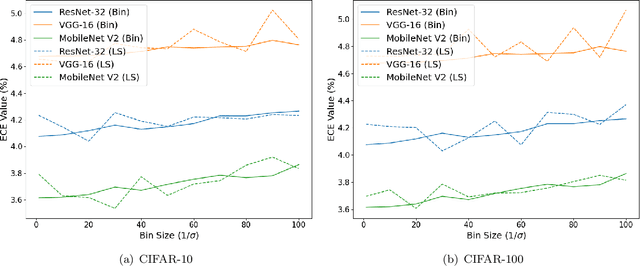
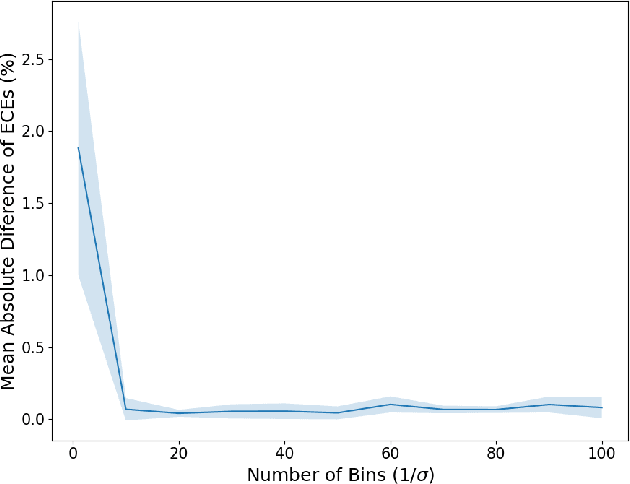
Informally, a model is calibrated if its predictions are correct with a probability that matches the confidence of the prediction. By far the most common method in the literature for measuring calibration is the expected calibration error (ECE). Recent work, however, has pointed out drawbacks of ECE, such as the fact that it is discontinuous in the space of predictors. In this work, we ask: how fundamental are these issues, and what are their impacts on existing results? Towards this end, we completely characterize the discontinuities of ECE with respect to general probability measures on Polish spaces. We then use the nature of these discontinuities to motivate a novel continuous, easily estimated miscalibration metric, which we term Logit-Smoothed ECE (LS-ECE). By comparing the ECE and LS-ECE of pre-trained image classification models, we show in initial experiments that binned ECE closely tracks LS-ECE, indicating that the theoretical pathologies of ECE may be avoidable in practice.

Principled Gradient-based Markov Chain Monte Carlo for Text Generation

Recent papers have demonstrated the possibility of energy-based text generation by adapting gradient-based sampling algorithms, a paradigm of MCMC algorithms that promises fast convergence. However, as we show in this paper, previous attempts on this approach to text generation all fail to sample correctly from the target language model distributions. To address this limitation, we consider the problem of designing text samplers that are faithful, meaning that they have the target text distribution as its limiting distribution. We propose several faithful gradient-based sampling algorithms to sample from the target energy-based text distribution correctly, and study their theoretical properties. Through experiments on various forms of text generation, we demonstrate that faithful samplers are able to generate more fluent text while adhering to the control objectives better.

Provable benefits of score matching

Score matching is an alternative to maximum likelihood (ML) for estimating a probability distribution parametrized up to a constant of proportionality. By fitting the ''score'' of the distribution, it sidesteps the need to compute this constant of proportionality (which is often intractable). While score matching and variants thereof are popular in practice, precise theoretical understanding of the benefits and tradeoffs with maximum likelihood -- both computational and statistical -- are not well understood. In this work, we give the first example of a natural exponential family of distributions such that the score matching loss is computationally efficient to optimize, and has a comparable statistical efficiency to ML, while the ML loss is intractable to optimize using a gradient-based method. The family consists of exponentials of polynomials of fixed degree, and our result can be viewed as a continuous analogue of recent developments in the discrete setting. Precisely, we show: (1) Designing a zeroth-order or first-order oracle for optimizing the maximum likelihood loss is NP-hard. (2) Maximum likelihood has a statistical efficiency polynomial in the ambient dimension and the radius of the parameters of the family. (3) Minimizing the score matching loss is both computationally and statistically efficient, with complexity polynomial in the ambient dimension.

The probability flow ODE is provably fast

We provide the first polynomial-time convergence guarantees for the probability flow ODE implementation (together with a corrector step) of score-based generative modeling. Our analysis is carried out in the wake of recent results obtaining such guarantees for the SDE-based implementation (i.e., denoising diffusion probabilistic modeling or DDPM), but requires the development of novel techniques for studying deterministic dynamics without contractivity. Through the use of a specially chosen corrector step based on the underdamped Langevin diffusion, we obtain better dimension dependence than prior works on DDPM ($O(\sqrt{d})$ vs. $O(d)$, assuming smoothness of the data distribution), highlighting potential advantages of the ODE framework.

Improved Bound for Mixing Time of Parallel Tempering

In the field of sampling algorithms, MCMC (Markov Chain Monte Carlo) methods are widely used when direct sampling is not possible. However, multimodality of target distributions often leads to slow convergence and mixing. One common solution is parallel tempering. Though highly effective in practice, theoretical guarantees on its performance are limited. In this paper, we present a new lower bound for parallel tempering on the spectral gap that has a polynomial dependence on all parameters except $\log L$, where $(L + 1)$ is the number of levels. This improves the best existing bound which depends exponentially on the number of modes. Moreover, we complement our result with a hypothetical upper bound on spectral gap that has an exponential dependence on $\log L$, which shows that, in some sense, our bound is tight.

Improved Analysis of Score-based Generative Modeling: User-Friendly Bounds under Minimal Smoothness Assumptions

In this paper, we focus on the theoretical analysis of diffusion-based generative modeling. Under an $L^2$-accurate score estimator, we provide convergence guarantees with polynomial complexity for any data distribution with second-order moment, by either employing an early stopping technique or assuming smoothness condition on the score function of the data distribution. Our result does not rely on any log-concavity or functional inequality assumption and has a logarithmic dependence on the smoothness. In particular, we show that under only a finite second moment condition, approximating the following in KL divergence in $\epsilon$-accuracy can be done in $\tilde O\left(\frac{d^2 \log^2 (1/\delta)}{\epsilon^2}\right)$ steps: 1) the variance-$\delta$ Gaussian perturbation of any data distribution; 2) data distributions with $1/\delta$-smooth score functions. Our theoretical analysis also provides quantitative comparison between different discrete approximations and may guide the choice of discretization points in practice.