Computational Dynamical Systems

We study the computational complexity theory of smooth, finite-dimensional dynamical systems. Building off of previous work, we give definitions for what it means for a smooth dynamical system to simulate a Turing machine. We then show that 'chaotic' dynamical systems (more precisely, Axiom A systems) and 'integrable' dynamical systems (more generally, measure-preserving systems) cannot robustly simulate universal Turing machines, although such machines can be robustly simulated by other kinds of dynamical systems. Subsequently, we show that any Turing machine that can be encoded into a structurally stable one-dimensional dynamical system must have a decidable halting problem, and moreover an explicit time complexity bound in instances where it does halt. More broadly, our work elucidates what it means for one 'machine' to simulate another, and emphasizes the necessity of defining low-complexity 'encoders' and 'decoders' to translate between the dynamics of the simulation and the system being simulated. We highlight how the notion of a computational dynamical system leads to questions at the intersection of computational complexity theory, dynamical systems theory, and real algebraic geometry.

How Flawed is ECE? An Analysis via Logit Smoothing

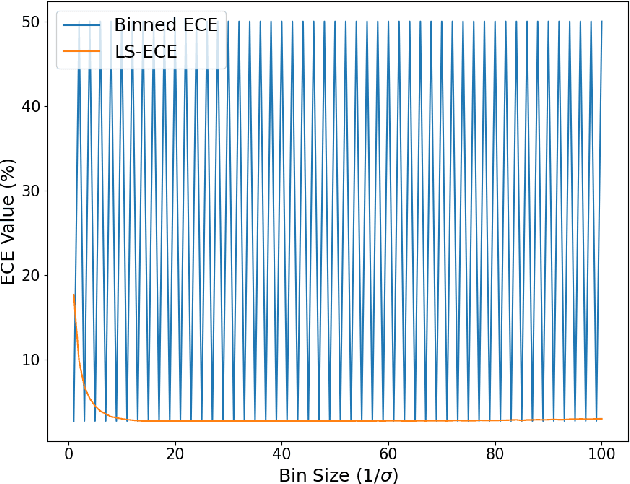
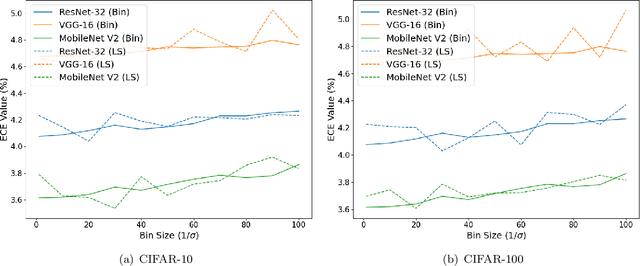
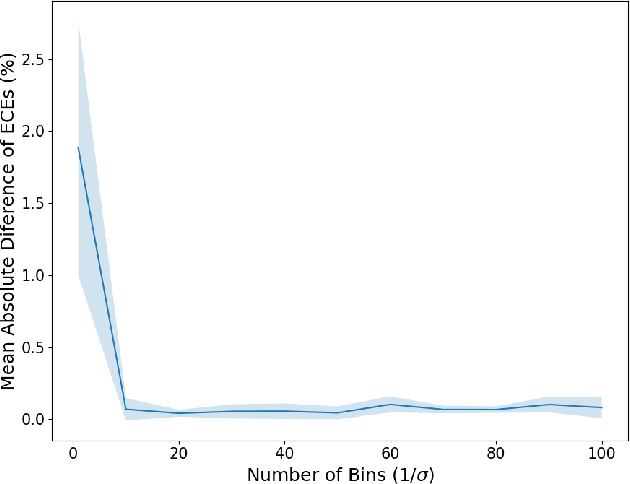
Informally, a model is calibrated if its predictions are correct with a probability that matches the confidence of the prediction. By far the most common method in the literature for measuring calibration is the expected calibration error (ECE). Recent work, however, has pointed out drawbacks of ECE, such as the fact that it is discontinuous in the space of predictors. In this work, we ask: how fundamental are these issues, and what are their impacts on existing results? Towards this end, we completely characterize the discontinuities of ECE with respect to general probability measures on Polish spaces. We then use the nature of these discontinuities to motivate a novel continuous, easily estimated miscalibration metric, which we term Logit-Smoothed ECE (LS-ECE). By comparing the ECE and LS-ECE of pre-trained image classification models, we show in initial experiments that binned ECE closely tracks LS-ECE, indicating that the theoretical pathologies of ECE may be avoidable in practice.

Renormalizing Diffusion Models

We explain how to use diffusion models to learn inverse renormalization group flows of statistical and quantum field theories. Diffusion models are a class of machine learning models which have been used to generate samples from complex distributions, such as the distribution of natural images. These models achieve sample generation by learning the inverse process to a diffusion process which adds noise to the data until the distribution of the data is pure noise. Nonperturbative renormalization group schemes in physics can naturally be written as diffusion processes in the space of fields. We combine these observations in a concrete framework for building ML-based models for studying field theories, in which the models learn the inverse process to an explicitly-specified renormalization group scheme. We detail how these models define a class of adaptive bridge (or parallel tempering) samplers for lattice field theory. Because renormalization group schemes have a physical meaning, we provide explicit prescriptions for how to compare results derived from models associated to several different renormalization group schemes of interest. We also explain how to use diffusion models in a variational method to find ground states of quantum systems. We apply some of our methods to numerically find RG flows of interacting statistical field theories. From the perspective of machine learning, our work provides an interpretation of multiscale diffusion models, and gives physically-inspired suggestions for diffusion models which should have novel properties.

Diffusion with Forward Models: Solving Stochastic Inverse Problems Without Direct Supervision

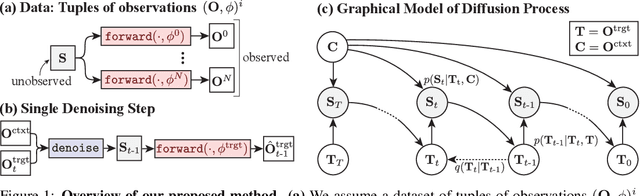
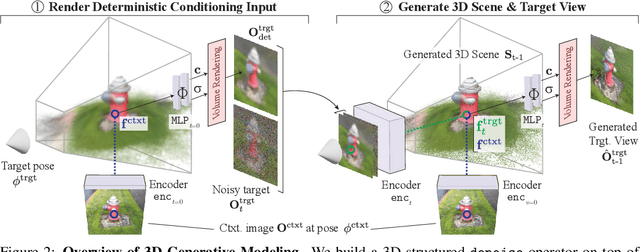
Denoising diffusion models are a powerful type of generative models used to capture complex distributions of real-world signals. However, their applicability is limited to scenarios where training samples are readily available, which is not always the case in real-world applications. For example, in inverse graphics, the goal is to generate samples from a distribution of 3D scenes that align with a given image, but ground-truth 3D scenes are unavailable and only 2D images are accessible. To address this limitation, we propose a novel class of denoising diffusion probabilistic models that learn to sample from distributions of signals that are never directly observed. Instead, these signals are measured indirectly through a known differentiable forward model, which produces partial observations of the unknown signal. Our approach involves integrating the forward model directly into the denoising process. This integration effectively connects the generative modeling of observations with the generative modeling of the underlying signals, allowing for end-to-end training of a conditional generative model over signals. During inference, our approach enables sampling from the distribution of underlying signals that are consistent with a given partial observation. We demonstrate the effectiveness of our method on three challenging computer vision tasks. For instance, in the context of inverse graphics, our model enables direct sampling from the distribution of 3D scenes that align with a single 2D input image.

Light Field Networks: Neural Scene Representations with Single-Evaluation Rendering

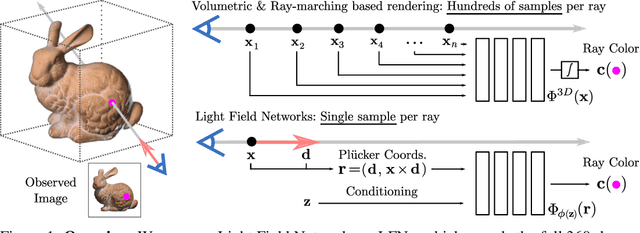
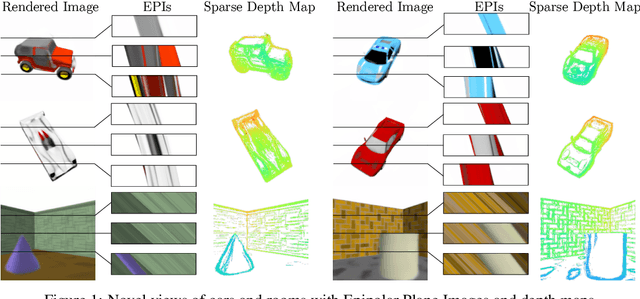
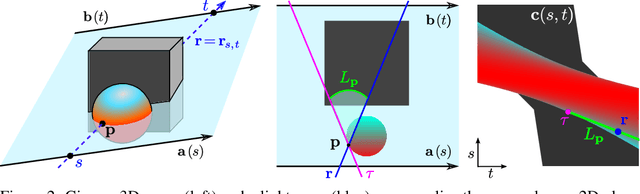
Inferring representations of 3D scenes from 2D observations is a fundamental problem of computer graphics, computer vision, and artificial intelligence. Emerging 3D-structured neural scene representations are a promising approach to 3D scene understanding. In this work, we propose a novel neural scene representation, Light Field Networks or LFNs, which represent both geometry and appearance of the underlying 3D scene in a 360-degree, four-dimensional light field parameterized via a neural implicit representation. Rendering a ray from an LFN requires only a *single* network evaluation, as opposed to hundreds of evaluations per ray for ray-marching or volumetric based renderers in 3D-structured neural scene representations. In the setting of simple scenes, we leverage meta-learning to learn a prior over LFNs that enables multi-view consistent light field reconstruction from as little as a single image observation. This results in dramatic reductions in time and memory complexity, and enables real-time rendering. The cost of storing a 360-degree light field via an LFN is two orders of magnitude lower than conventional methods such as the Lumigraph. Utilizing the analytical differentiability of neural implicit representations and a novel parameterization of light space, we further demonstrate the extraction of sparse depth maps from LFNs.

Stochastic natural gradient descent draws posterior samples in function space

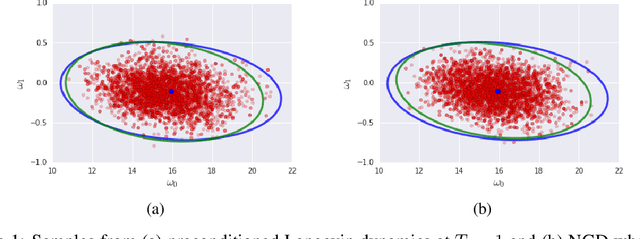
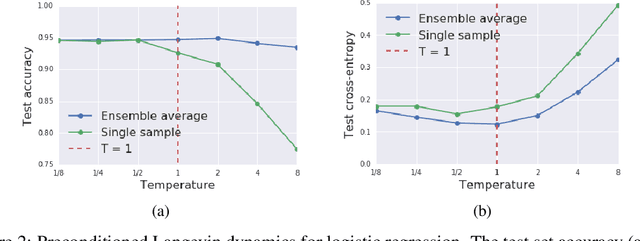
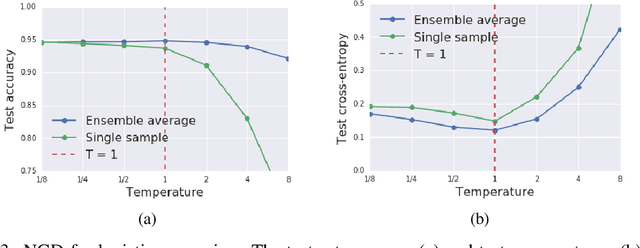
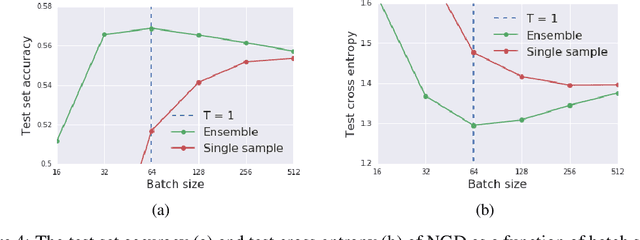
We prove that as the model predictions on the training set approach the true conditional distribution of labels given inputs, the noise inherent in minibatch gradients causes the stationary distribution of natural gradient descent to approach a Bayesian posterior near local minima as the learning rate $\epsilon \rightarrow 0$. The temperature $T \approx \epsilon N/(2B)$ of this posterior is controlled by the learning rate, training set size $N$ and batch size $B$. However minibatch NGD is not parameterisation invariant, and we therefore introduce "stochastic natural gradient descent", which preserves parameterisation invariance by introducing a multiplicative bias to the stationary distribution. We identify this bias as the well known Jeffreys prior. To support our claims, we show that the distribution of samples from NGD is close to the Laplace approximation to the posterior when $T = 1$. Furthermore, the test loss of ensembles drawn using NGD falls rapidly as we increase the batch size until $B \approx \epsilon N/2$, while above this point the test loss is constant or rises slowly.