Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Reassessing How to Compare and Improve the Calibration of Machine Learning Models

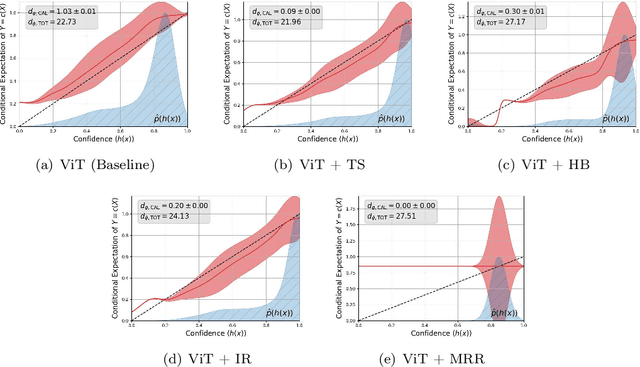
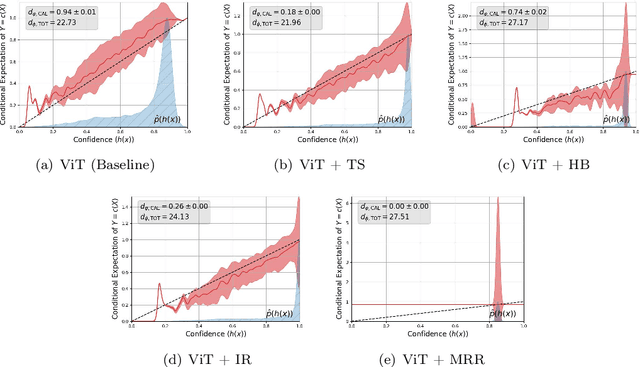
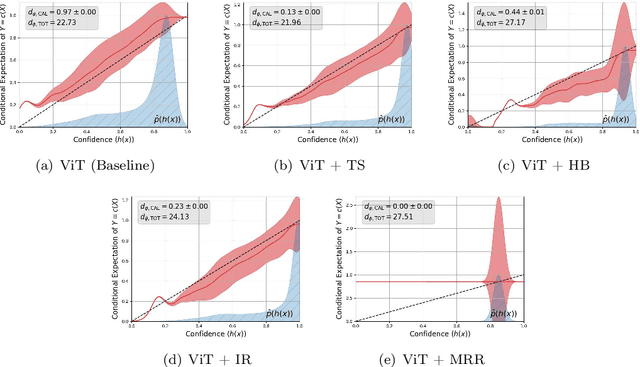
A machine learning model is calibrated if its predicted probability for an outcome matches the observed frequency for that outcome conditional on the model prediction. This property has become increasingly important as the impact of machine learning models has continued to spread to various domains. As a result, there are now a dizzying number of recent papers on measuring and improving the calibration of (specifically deep learning) models. In this work, we reassess the reporting of calibration metrics in the recent literature. We show that there exist trivial recalibration approaches that can appear seemingly state-of-the-art unless calibration and prediction metrics (i.e. test accuracy) are accompanied by additional generalization metrics such as negative log-likelihood. We then derive a calibration-based decomposition of Bregman divergences that can be used to both motivate a choice of calibration metric based on a generalization metric, and to detect trivial calibration. Finally, we apply these ideas to develop a new extension to reliability diagrams that can be used to jointly visualize calibration as well as the estimated generalization error of a model.

How Flawed is ECE? An Analysis via Logit Smoothing

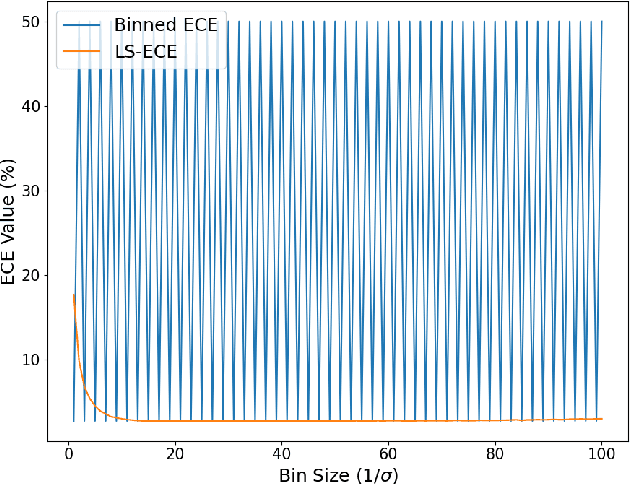
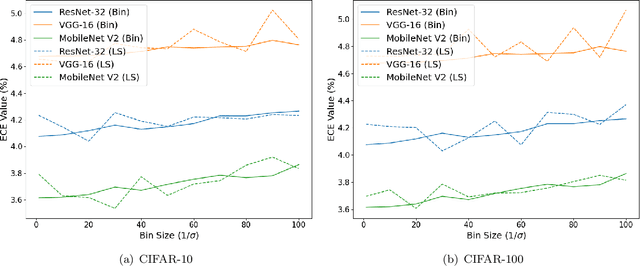
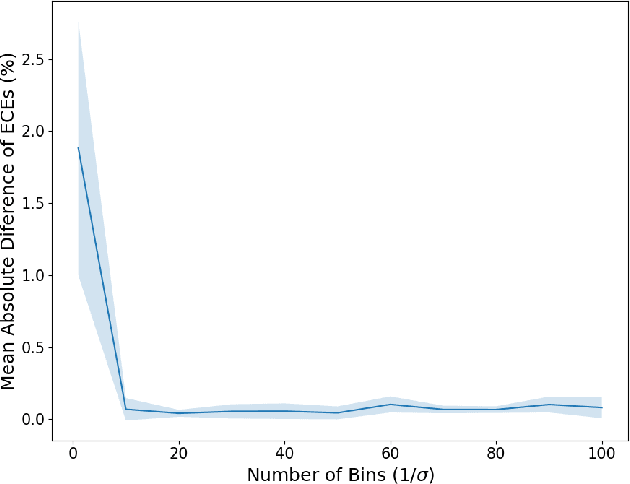
Informally, a model is calibrated if its predictions are correct with a probability that matches the confidence of the prediction. By far the most common method in the literature for measuring calibration is the expected calibration error (ECE). Recent work, however, has pointed out drawbacks of ECE, such as the fact that it is discontinuous in the space of predictors. In this work, we ask: how fundamental are these issues, and what are their impacts on existing results? Towards this end, we completely characterize the discontinuities of ECE with respect to general probability measures on Polish spaces. We then use the nature of these discontinuities to motivate a novel continuous, easily estimated miscalibration metric, which we term Logit-Smoothed ECE (LS-ECE). By comparing the ECE and LS-ECE of pre-trained image classification models, we show in initial experiments that binned ECE closely tracks LS-ECE, indicating that the theoretical pathologies of ECE may be avoidable in practice.

For Better or For Worse? Learning Minimum Variance Features With Label Augmentation

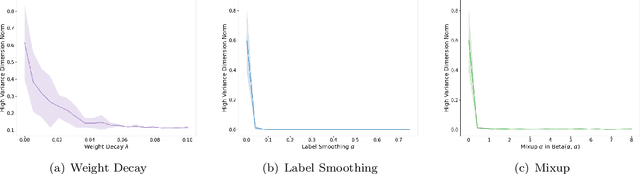
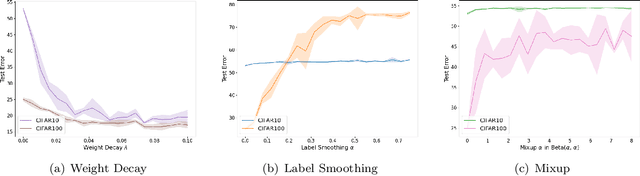
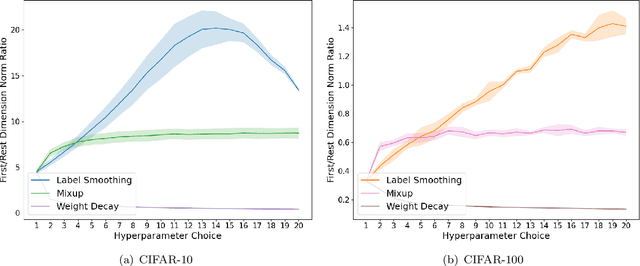
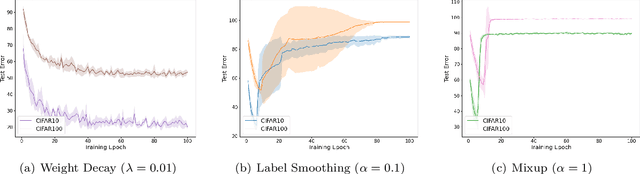
Data augmentation has been pivotal in successfully training deep learning models on classification tasks over the past decade. An important subclass of data augmentation techniques - which includes both label smoothing and Mixup - involves modifying not only the input data but also the input label during model training. In this work, we analyze the role played by the label augmentation aspect of such methods. We prove that linear models on linearly separable data trained with label augmentation learn only the minimum variance features in the data, while standard training (which includes weight decay) can learn higher variance features. An important consequence of our results is negative: label smoothing and Mixup can be less robust to adversarial perturbations of the training data when compared to standard training. We verify that our theory reflects practice via a range of experiments on synthetic data and image classification benchmarks.

A Uniform Confidence Phenomenon in Deep Learning and its Implications for Calibration

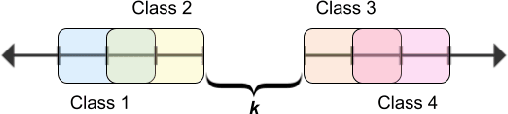
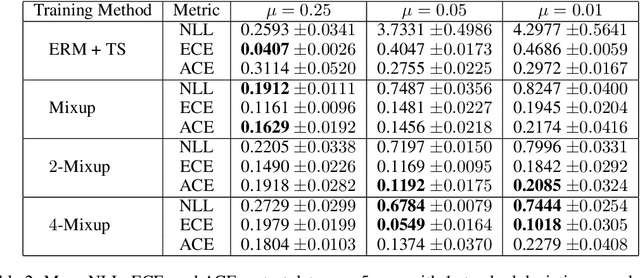
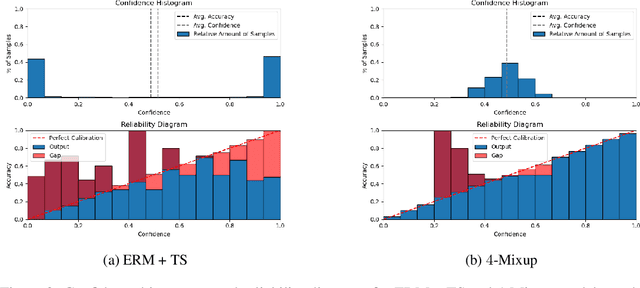
Despite the impressive generalization capabilities of deep neural networks, they have been repeatedly shown to poorly estimate their predictive uncertainty - in other words, they are frequently overconfident when they are wrong. Fixing this issue is known as model calibration, and has consequently received much attention in the form of modified training schemes and post-training calibration procedures. In this work, we present a significant hurdle to the calibration of modern models: deep neural networks have large neighborhoods of almost certain confidence around their training points. We demonstrate in our experiments that this phenomenon consistently arises (in the context of image classification) across many model and dataset pairs. Furthermore, we prove that when this phenomenon holds, for a large class of data distributions with overlaps between classes, it is not possible to obtain a model that is asymptotically better than random (with respect to calibration) even after applying the standard post-training calibration technique of temperature scaling. On the other hand, we also prove that it is possible to circumvent this defect by changing the training process to use a modified loss based on the Mixup data augmentation technique.

Hiding Data Helps: On the Benefits of Masking for Sparse Coding

Sparse coding refers to modeling a signal as sparse linear combinations of the elements of a learned dictionary. Sparse coding has proven to be a successful and interpretable approach in many applications, such as signal processing, computer vision, and medical imaging. While this success has spurred much work on sparse coding with provable guarantees, work on the setting where the learned dictionary is larger (or \textit{over-realized}) with respect to the ground truth is comparatively nascent. Existing theoretical results in the over-realized regime are limited to the case of noise-less data. In this paper, we show that for over-realized sparse coding in the presence of noise, minimizing the standard dictionary learning objective can fail to recover the ground-truth dictionary, regardless of the magnitude of the signal in the data-generating process. Furthermore, drawing from the growing body of work on self-supervised learning, we propose a novel masking objective and we prove that minimizing this new objective can recover the ground-truth dictionary. We corroborate our theoretical results with experiments across several parameter regimes, showing that our proposed objective enjoys better empirical performance than the standard reconstruction objective.

Provably Learning Diverse Features in Multi-View Data with Midpoint Mixup

Mixup is a data augmentation technique that relies on training using random convex combinations of data points and their labels. In recent years, Mixup has become a standard primitive used in the training of state-of-the-art image classification models due to its demonstrated benefits over empirical risk minimization with regards to generalization and robustness. In this work, we try to explain some of this success from a feature learning perspective. We focus our attention on classification problems in which each class may have multiple associated features (or views) that can be used to predict the class correctly. Our main theoretical results demonstrate that, for a non-trivial class of data distributions with two features per class, training a 2-layer convolutional network using empirical risk minimization can lead to learning only one feature for almost all classes while training with a specific instantiation of Mixup succeeds in learning both features for every class. We also show empirically that these theoretical insights extend to the practical settings of image benchmarks modified to have additional synthetic features.

Towards Understanding the Data Dependency of Mixup-style Training

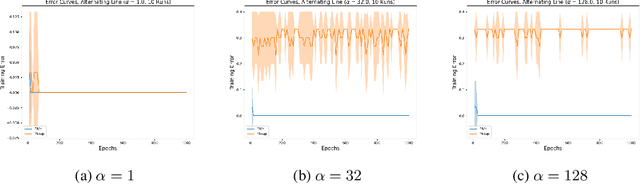
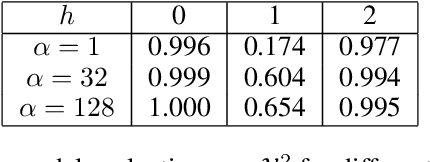
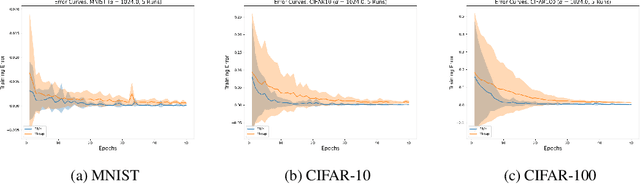
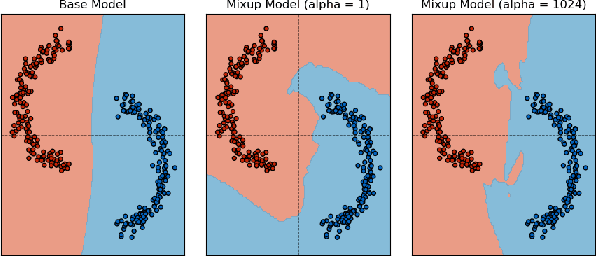
In the Mixup training paradigm, a model is trained using convex combinations of data points and their associated labels. Despite seeing very few true data points during training, models trained using Mixup seem to still minimize the original empirical risk and exhibit better generalization and robustness on various tasks when compared to standard training. In this paper, we investigate how these benefits of Mixup training rely on properties of the data in the context of classification. For minimizing the original empirical risk, we compute a closed form for the Mixup-optimal classification, which allows us to construct a simple dataset on which minimizing the Mixup loss can provably lead to learning a classifier that does not minimize the empirical loss on the data. On the other hand, we also give sufficient conditions for Mixup training to also minimize the original empirical risk. For generalization, we characterize the margin of a Mixup classifier, and use this to understand why the decision boundary of a Mixup classifier can adapt better to the full structure of the training data when compared to standard training. In contrast, we also show that, for a large class of linear models and linearly separable datasets, Mixup training leads to learning the same classifier as standard training.