Stochastic natural gradient descent draws posterior samples in function space

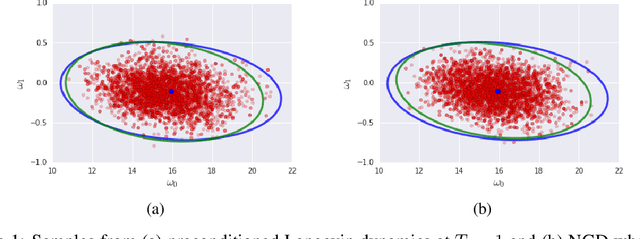
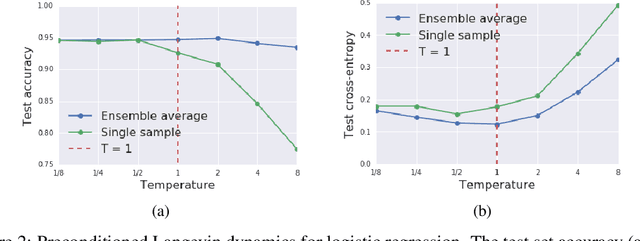
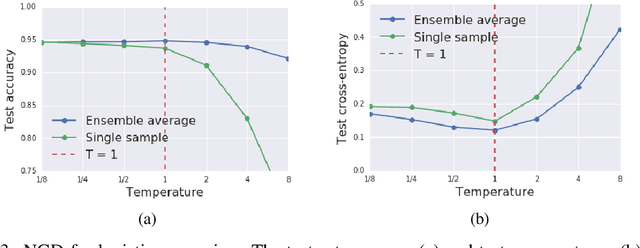
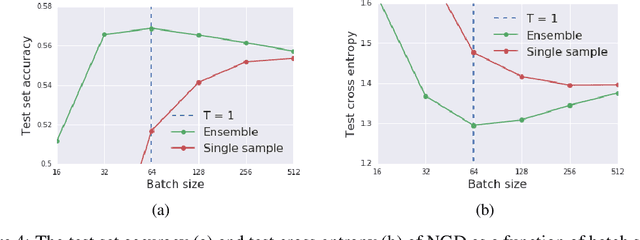
We prove that as the model predictions on the training set approach the true conditional distribution of labels given inputs, the noise inherent in minibatch gradients causes the stationary distribution of natural gradient descent to approach a Bayesian posterior near local minima as the learning rate $\epsilon \rightarrow 0$. The temperature $T \approx \epsilon N/(2B)$ of this posterior is controlled by the learning rate, training set size $N$ and batch size $B$. However minibatch NGD is not parameterisation invariant, and we therefore introduce "stochastic natural gradient descent", which preserves parameterisation invariance by introducing a multiplicative bias to the stationary distribution. We identify this bias as the well known Jeffreys prior. To support our claims, we show that the distribution of samples from NGD is close to the Laplace approximation to the posterior when $T = 1$. Furthermore, the test loss of ensembles drawn using NGD falls rapidly as we increase the batch size until $B \approx \epsilon N/2$, while above this point the test loss is constant or rises slowly.