Multi-scale Topology Optimization using Neural Networks

A long-standing challenge is designing multi-scale structures with good connectivity between cells while optimizing each cell to reach close to the theoretical performance limit. We propose a new method for direct multi-scale topology optimization using neural networks. Our approach focuses on inverse homogenization that seamlessly maintains compatibility across neighboring microstructure cells. Our approach consists of a topology neural network that optimizes the microstructure shape and distribution across the design domain as a continuous field. Each microstructure cell is optimized based on a specified elasticity tensor that also accommodates in-plane rotations. The neural network takes as input the local coordinates within a cell to represent the density distribution within a cell, as well as the global coordinates of each cell to design spatially varying microstructure cells. As such, our approach models an n-dimensional multi-scale optimization problem as a 2n-dimensional inverse homogenization problem using neural networks. During the inverse homogenization of each unit cell, we extend the boundary of each cell by scaling the input coordinates such that the boundaries of neighboring cells are combined. Inverse homogenization on the combined cell improves connectivity. We demonstrate our method through the design and optimization of graded multi-scale structures.

Convergence Analysis of Discrete Diffusion Model: Exact Implementation through Uniformization

Diffusion models have achieved huge empirical success in data generation tasks. Recently, some efforts have been made to adapt the framework of diffusion models to discrete state space, providing a more natural approach for modeling intrinsically discrete data, such as language and graphs. This is achieved by formulating both the forward noising process and the corresponding reversed process as Continuous Time Markov Chains (CTMCs). In this paper, we investigate the theoretical properties of the discrete diffusion model. Specifically, we introduce an algorithm leveraging the uniformization of continuous Markov chains, implementing transitions on random time points. Under reasonable assumptions on the learning of the discrete score function, we derive Total Variation distance and KL divergence guarantees for sampling from any distribution on a hypercube. Our results align with state-of-the-art achievements for diffusion models in $\mathbb{R}^d$ and further underscore the advantages of discrete diffusion models in comparison to the $\mathbb{R}^d$ setting.

BackdoorBench: A Comprehensive Benchmark and Analysis of Backdoor Learning

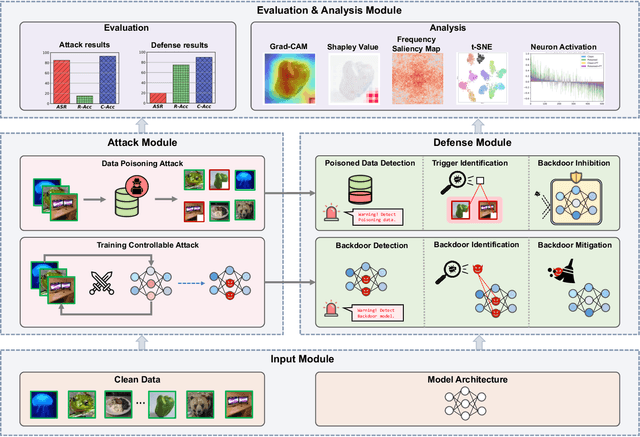
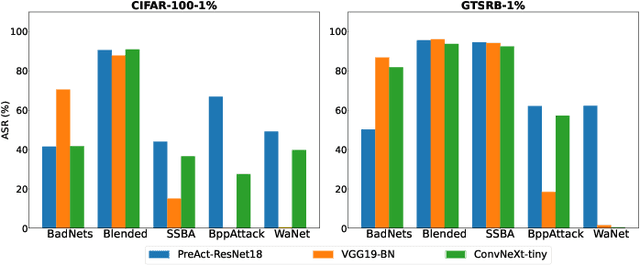
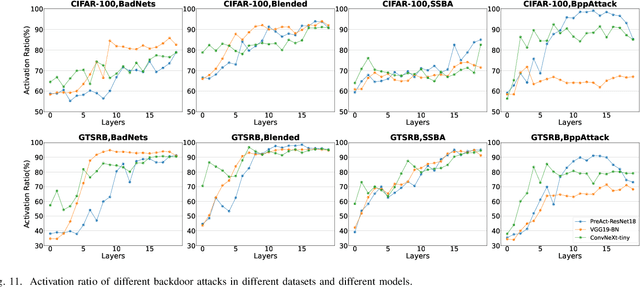
As an emerging and vital topic for studying deep neural networks' vulnerability (DNNs), backdoor learning has attracted increasing interest in recent years, and many seminal backdoor attack and defense algorithms are being developed successively or concurrently, in the status of a rapid arms race. However, mainly due to the diverse settings, and the difficulties of implementation and reproducibility of existing works, there is a lack of a unified and standardized benchmark of backdoor learning, causing unfair comparisons, and unreliable conclusions (e.g., misleading, biased or even false conclusions). Consequently, it is difficult to evaluate the current progress and design the future development roadmap of this literature. To alleviate this dilemma, we build a comprehensive benchmark of backdoor learning called BackdoorBench. Our benchmark makes three valuable contributions to the research community. 1) We provide an integrated implementation of state-of-the-art (SOTA) backdoor learning algorithms (currently including 16 attack and 27 defense algorithms), based on an extensible modular-based codebase. 2) We conduct comprehensive evaluations of 12 attacks against 16 defenses, with 5 poisoning ratios, based on 4 models and 4 datasets, thus 11,492 pairs of evaluations in total. 3) Based on above evaluations, we present abundant analysis from 8 perspectives via 18 useful analysis tools, and provide several inspiring insights about backdoor learning. We hope that our efforts could build a solid foundation of backdoor learning to facilitate researchers to investigate existing algorithms, develop more innovative algorithms, and explore the intrinsic mechanism of backdoor learning. Finally, we have created a user-friendly website at http://backdoorbench.com, which collects all important information of BackdoorBench, including codebase, docs, leaderboard, and model Zoo.

Defenses in Adversarial Machine Learning: A Survey

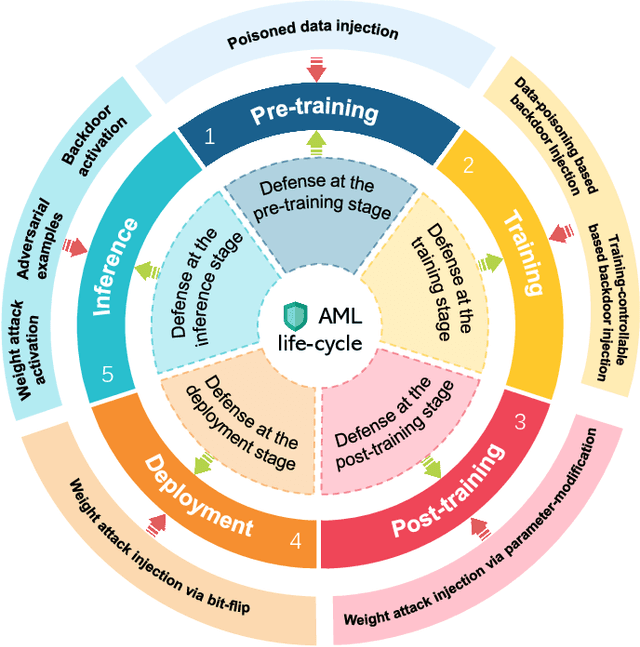
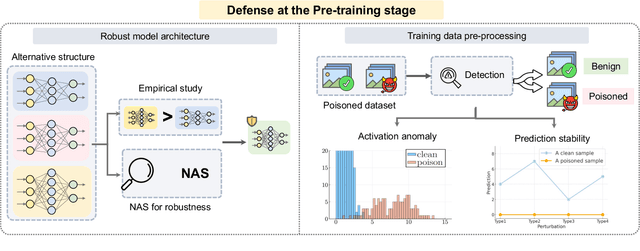
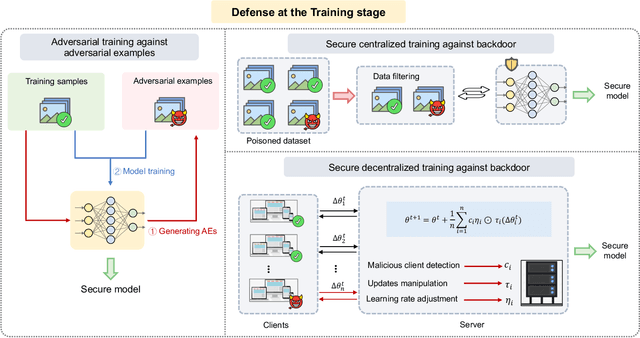
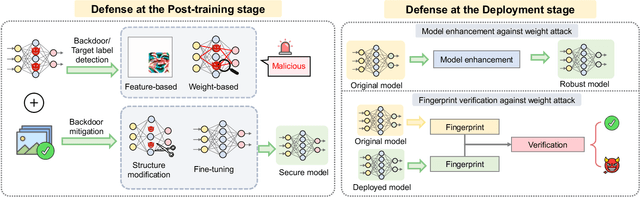
Adversarial phenomenon has been widely observed in machine learning (ML) systems, especially in those using deep neural networks, describing that ML systems may produce inconsistent and incomprehensible predictions with humans at some particular cases. This phenomenon poses a serious security threat to the practical application of ML systems, and several advanced attack paradigms have been developed to explore it, mainly including backdoor attacks, weight attacks, and adversarial examples. For each individual attack paradigm, various defense paradigms have been developed to improve the model robustness against the corresponding attack paradigm. However, due to the independence and diversity of these defense paradigms, it is difficult to examine the overall robustness of an ML system against different kinds of attacks.This survey aims to build a systematic review of all existing defense paradigms from a unified perspective. Specifically, from the life-cycle perspective, we factorize a complete machine learning system into five stages, including pre-training, training, post-training, deployment, and inference stages, respectively. Then, we present a clear taxonomy to categorize and review representative defense methods at each individual stage. The unified perspective and presented taxonomies not only facilitate the analysis of the mechanism of each defense paradigm but also help us to understand connections and differences among different defense paradigms, which may inspire future research to develop more advanced, comprehensive defenses.

The $L^\infty$ Learnability of Reproducing Kernel Hilbert Spaces

In this work, we analyze the learnability of reproducing kernel Hilbert spaces (RKHS) under the $L^\infty$ norm, which is critical for understanding the performance of kernel methods and random feature models in safety- and security-critical applications. Specifically, we relate the $L^\infty$ learnability of a RKHS to the spectrum decay of the associate kernel and both lower bounds and upper bounds of the sample complexity are established. In particular, for dot-product kernels on the sphere, we identify conditions when the $L^\infty$ learning can be achieved with polynomial samples. Let $d$ denote the input dimension and assume the kernel spectrum roughly decays as $\lambda_k\sim k^{-1-\beta}$ with $\beta>0$. We prove that if $\beta$ is independent of the input dimension $d$, then functions in the RKHS can be learned efficiently under the $L^\infty$ norm, i.e., the sample complexity depends polynomially on $d$. In contrast, if $\beta=1/\mathrm{poly}(d)$, then the $L^\infty$ learning requires exponentially many samples.

Robust Backdoor Attack with Visible, Semantic, Sample-Specific, and Compatible Triggers

Deep neural networks (DNNs) can be manipulated to exhibit specific behaviors when exposed to specific trigger patterns, without affecting their performance on normal samples. This type of attack is known as a backdoor attack. Recent research has focused on designing invisible triggers for backdoor attacks to ensure visual stealthiness. These triggers have demonstrated strong attack performance even under backdoor defense, which aims to eliminate or suppress the backdoor effect in the model. However, through experimental observations, we have noticed that these carefully designed invisible triggers are often susceptible to visual distortion during inference, such as Gaussian blurring or environmental variations in real-world scenarios. This phenomenon significantly undermines the effectiveness of attacks in practical applications. Unfortunately, this issue has not received sufficient attention and has not been thoroughly investigated. To address this limitation, we propose a novel approach called the Visible, Semantic, Sample-Specific, and Compatible trigger (VSSC-trigger), which leverages a recent powerful image method known as the stable diffusion model. In this approach, a text trigger is utilized as a prompt and combined with a benign image. The resulting combination is then processed by a pre-trained stable diffusion model, generating a corresponding semantic object. This object is seamlessly integrated with the original image, resulting in a new realistic image, referred to as the poisoned image. Extensive experimental results and analysis validate the effectiveness and robustness of our proposed attack method, even in the presence of visual distortion. We believe that the new trigger proposed in this work, along with the proposed idea to address the aforementioned issues, will have significant prospective implications for further advancements in this direction.

Topology Optimization using Neural Networks with Conditioning Field Initialization for Improved Efficiency

We propose conditioning field initialization for neural network based topology optimization. In this work, we focus on (1) improving upon existing neural network based topology optimization, (2) demonstrating that by using a prior initial field on the unoptimized domain, the efficiency of neural network based topology optimization can be further improved. Our approach consists of a topology neural network that is trained on a case by case basis to represent the geometry for a single topology optimization problem. It takes in domain coordinates as input to represent the density at each coordinate where the topology is represented by a continuous density field. The displacement is solved through a finite element solver. We employ the strain energy field calculated on the initial design domain as an additional conditioning field input to the neural network throughout the optimization. The addition of the strain energy field input improves the convergence speed compared to standalone neural network based topology optimization.

A duality framework for generalization analysis of random feature models and two-layer neural networks

We consider the problem of learning functions in the $\mathcal{F}_{p,\pi}$ and Barron spaces, which are natural function spaces that arise in the high-dimensional analysis of random feature models (RFMs) and two-layer neural networks. Through a duality analysis, we reveal that the approximation and estimation of these spaces can be considered equivalent in a certain sense. This enables us to focus on the easier problem of approximation and estimation when studying the generalization of both models. The dual equivalence is established by defining an information-based complexity that can effectively control estimation errors. Additionally, we demonstrate the flexibility of our duality framework through comprehensive analyses of two concrete applications. The first application is to study learning functions in $\mathcal{F}_{p,\pi}$ with RFMs. We prove that the learning does not suffer from the curse of dimensionality as long as $p>1$, implying RFMs can work beyond the kernel regime. Our analysis extends existing results [CMM21] to the noisy case and removes the requirement of overparameterization. The second application is to investigate the learnability of reproducing kernel Hilbert space (RKHS) under the $L^\infty$ metric. We derive both lower and upper bounds of the minimax estimation error by using the spectrum of the associated kernel. We then apply these bounds to dot-product kernels and analyze how they scale with the input dimension. Our results suggest that learning with ReLU (random) features is generally intractable in terms of reaching high uniform accuracy.

DMF-TONN: Direct Mesh-free Topology Optimization using Neural Networks

We propose a direct mesh-free method for performing topology optimization by integrating a density field approximation neural network with a displacement field approximation neural network. We show that this direct integration approach can give comparable results to conventional topology optimization techniques, with an added advantage of enabling seamless integration with post-processing software, and a potential of topology optimization with objectives where meshing and Finite Element Analysis (FEA) may be expensive or not suitable. Our approach (DMF-TONN) takes in as inputs the boundary conditions and domain coordinates and finds the optimum density field for minimizing the loss function of compliance and volume fraction constraint violation. The mesh-free nature is enabled by a physics-informed displacement field approximation neural network to solve the linear elasticity partial differential equation and replace the FEA conventionally used for calculating the compliance. We show that using a suitable Fourier Features neural network architecture and hyperparameters, the density field approximation neural network can learn the weights to represent the optimal density field for the given domain and boundary conditions, by directly backpropagating the loss gradient through the displacement field approximation neural network, and unlike prior work there is no requirement of a sensitivity filter, optimality criterion method, or a separate training of density network in each topology optimization iteration.

Improved Analysis of Score-based Generative Modeling: User-Friendly Bounds under Minimal Smoothness Assumptions

In this paper, we focus on the theoretical analysis of diffusion-based generative modeling. Under an $L^2$-accurate score estimator, we provide convergence guarantees with polynomial complexity for any data distribution with second-order moment, by either employing an early stopping technique or assuming smoothness condition on the score function of the data distribution. Our result does not rely on any log-concavity or functional inequality assumption and has a logarithmic dependence on the smoothness. In particular, we show that under only a finite second moment condition, approximating the following in KL divergence in $\epsilon$-accuracy can be done in $\tilde O\left(\frac{d^2 \log^2 (1/\delta)}{\epsilon^2}\right)$ steps: 1) the variance-$\delta$ Gaussian perturbation of any data distribution; 2) data distributions with $1/\delta$-smooth score functions. Our theoretical analysis also provides quantitative comparison between different discrete approximations and may guide the choice of discretization points in practice.