Efficiently learning and sampling multimodal distributions with data-based initialization

We consider the problem of sampling a multimodal distribution with a Markov chain given a small number of samples from the stationary measure. Although mixing can be arbitrarily slow, we show that if the Markov chain has a $k$th order spectral gap, initialization from a set of $\tilde O(k/\varepsilon^2)$ samples from the stationary distribution will, with high probability over the samples, efficiently generate a sample whose conditional law is $\varepsilon$-close in TV distance to the stationary measure. In particular, this applies to mixtures of $k$ distributions satisfying a Poincar\'e inequality, with faster convergence when they satisfy a log-Sobolev inequality. Our bounds are stable to perturbations to the Markov chain, and in particular work for Langevin diffusion over $\mathbb R^d$ with score estimation error, as well as Glauber dynamics combined with approximation error from pseudolikelihood estimation. This justifies the success of data-based initialization for score matching methods despite slow mixing for the data distribution, and improves and generalizes the results of Koehler and Vuong (2023) to have linear, rather than exponential, dependence on $k$ and apply to arbitrary semigroups. As a consequence of our results, we show for the first time that a natural class of low-complexity Ising measures can be efficiently learned from samples.

Fast parallel sampling under isoperimetry

We show how to sample in parallel from a distribution $\pi$ over $\mathbb R^d$ that satisfies a log-Sobolev inequality and has a smooth log-density, by parallelizing the Langevin (resp. underdamped Langevin) algorithms. We show that our algorithm outputs samples from a distribution $\hat\pi$ that is close to $\pi$ in Kullback--Leibler (KL) divergence (resp. total variation (TV) distance), while using only $\log(d)^{O(1)}$ parallel rounds and $\widetilde{O}(d)$ (resp. $\widetilde O(\sqrt d)$) gradient evaluations in total. This constitutes the first parallel sampling algorithms with TV distance guarantees. For our main application, we show how to combine the TV distance guarantees of our algorithms with prior works and obtain RNC sampling-to-counting reductions for families of discrete distribution on the hypercube $\{\pm 1\}^n$ that are closed under exponential tilts and have bounded covariance. Consequently, we obtain an RNC sampler for directed Eulerian tours and asymmetric determinantal point processes, resolving open questions raised in prior works.

Fairness in Submodular Maximization over a Matroid Constraint

Submodular maximization over a matroid constraint is a fundamental problem with various applications in machine learning. Some of these applications involve decision-making over datapoints with sensitive attributes such as gender or race. In such settings, it is crucial to guarantee that the selected solution is fairly distributed with respect to this attribute. Recently, fairness has been investigated in submodular maximization under a cardinality constraint in both the streaming and offline settings, however the more general problem with matroid constraint has only been considered in the streaming setting and only for monotone objectives. This work fills this gap. We propose various algorithms and impossibility results offering different trade-offs between quality, fairness, and generality.

Sampling Multimodal Distributions with the Vanilla Score: Benefits of Data-Based Initialization

There is a long history, as well as a recent explosion of interest, in statistical and generative modeling approaches based on score functions -- derivatives of the log-likelihood of a distribution. In seminal works, Hyv\"arinen proposed vanilla score matching as a way to learn distributions from data by computing an estimate of the score function of the underlying ground truth, and established connections between this method and established techniques like Contrastive Divergence and Pseudolikelihood estimation. It is by now well-known that vanilla score matching has significant difficulties learning multimodal distributions. Although there are various ways to overcome this difficulty, the following question has remained unanswered -- is there a natural way to sample multimodal distributions using just the vanilla score? Inspired by a long line of related experimental works, we prove that the Langevin diffusion with early stopping, initialized at the empirical distribution, and run on a score function estimated from data successfully generates natural multimodal distributions (mixtures of log-concave distributions).

Optimal Sublinear Sampling of Spanning Trees and Determinantal Point Processes via Average-Case Entropic Independence

We design fast algorithms for repeatedly sampling from strongly Rayleigh distributions, which include random spanning tree distributions and determinantal point processes. For a graph $G=(V, E)$, we show how to approximately sample uniformly random spanning trees from $G$ in $\widetilde{O}(\lvert V\rvert)$ time per sample after an initial $\widetilde{O}(\lvert E\rvert)$ time preprocessing. For a determinantal point process on subsets of size $k$ of a ground set of $n$ elements, we show how to approximately sample in $\widetilde{O}(k^\omega)$ time after an initial $\widetilde{O}(nk^{\omega-1})$ time preprocessing, where $\omega<2.372864$ is the matrix multiplication exponent. We even improve the state of the art for obtaining a single sample from determinantal point processes, from the prior runtime of $\widetilde{O}(\min\{nk^2, n^\omega\})$ to $\widetilde{O}(nk^{\omega-1})$. In our main technical result, we achieve the optimal limit on domain sparsification for strongly Rayleigh distributions. In domain sparsification, sampling from a distribution $\mu$ on $\binom{[n]}{k}$ is reduced to sampling from related distributions on $\binom{[t]}{k}$ for $t\ll n$. We show that for strongly Rayleigh distributions, we can can achieve the optimal $t=\widetilde{O}(k)$. Our reduction involves sampling from $\widetilde{O}(1)$ domain-sparsified distributions, all of which can be produced efficiently assuming convenient access to approximate overestimates for marginals of $\mu$. Having access to marginals is analogous to having access to the mean and covariance of a continuous distribution, or knowing "isotropy" for the distribution, the key assumption behind the Kannan-Lov\'asz-Simonovits (KLS) conjecture and optimal samplers based on it. We view our result as a moral analog of the KLS conjecture and its consequences for sampling, for discrete strongly Rayleigh measures.

Simple and Near-Optimal MAP Inference for Nonsymmetric DPPs

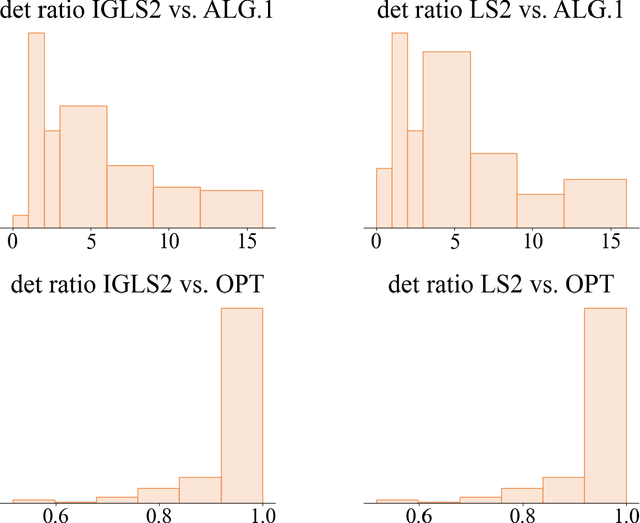
Determinantal point processes (DPPs) are widely popular probabilistic models used in machine learning to capture diversity in random subsets of items. While traditional DPPs are defined by a symmetric kernel matrix, recent work has shown a significant increase in the modeling power and applicability of models defined by nonsymmetric kernels, where the model can capture interactions that go beyond diversity. We study the problem of maximum a posteriori (MAP) inference for determinantal point processes defined by a nonsymmetric positive semidefinite matrix (NDPPs), where the goal is to find the maximum $k\times k$ principal minor of the kernel matrix $L$. We obtain the first multiplicative approximation guarantee for this problem using local search, a method that has been previously applied to symmetric DPPs. Our approximation factor of $k^{O(k)}$ is nearly tight, and we show theoretically and experimentally that it compares favorably to the state-of-the-art methods for this problem that are based on greedy maximization. The main new insight enabling our improved approximation factor is that we allow local search to update up to two elements of the solution in each iteration, and we show this is necessary to have any multiplicative approximation guarantee.