Consistent Submodular Maximization

Maximizing monotone submodular functions under cardinality constraints is a classic optimization task with several applications in data mining and machine learning. In this paper we study this problem in a dynamic environment with consistency constraints: elements arrive in a streaming fashion and the goal is maintaining a constant approximation to the optimal solution while having a stable solution (i.e., the number of changes between two consecutive solutions is bounded). We provide algorithms in this setting with different trade-offs between consistency and approximation quality. We also complement our theoretical results with an experimental analysis showing the effectiveness of our algorithms in real-world instances.

Fairness in Submodular Maximization over a Matroid Constraint

Submodular maximization over a matroid constraint is a fundamental problem with various applications in machine learning. Some of these applications involve decision-making over datapoints with sensitive attributes such as gender or race. In such settings, it is crucial to guarantee that the selected solution is fairly distributed with respect to this attribute. Recently, fairness has been investigated in submodular maximization under a cardinality constraint in both the streaming and offline settings, however the more general problem with matroid constraint has only been considered in the streaming setting and only for monotone objectives. This work fills this gap. We propose various algorithms and impossibility results offering different trade-offs between quality, fairness, and generality.

Fully Dynamic Submodular Maximization over Matroids

Maximizing monotone submodular functions under a matroid constraint is a classic algorithmic problem with multiple applications in data mining and machine learning. We study this classic problem in the fully dynamic setting, where elements can be both inserted and deleted in real-time. Our main result is a randomized algorithm that maintains an efficient data structure with an $\tilde{O}(k^2)$ amortized update time (in the number of additions and deletions) and yields a $4$-approximate solution, where $k$ is the rank of the matroid.

Fairness in Streaming Submodular Maximization over a Matroid Constraint

Streaming submodular maximization is a natural model for the task of selecting a representative subset from a large-scale dataset. If datapoints have sensitive attributes such as gender or race, it becomes important to enforce fairness to avoid bias and discrimination. This has spurred significant interest in developing fair machine learning algorithms. Recently, such algorithms have been developed for monotone submodular maximization under a cardinality constraint. In this paper, we study the natural generalization of this problem to a matroid constraint. We give streaming algorithms as well as impossibility results that provide trade-offs between efficiency, quality and fairness. We validate our findings empirically on a range of well-known real-world applications: exemplar-based clustering, movie recommendation, and maximum coverage in social networks.

Deletion Robust Non-Monotone Submodular Maximization over Matroids

Maximizing a submodular function is a fundamental task in machine learning and in this paper we study the deletion robust version of the problem under the classic matroids constraint. Here the goal is to extract a small size summary of the dataset that contains a high value independent set even after an adversary deleted some elements. We present constant-factor approximation algorithms, whose space complexity depends on the rank $k$ of the matroid and the number $d$ of deleted elements. In the centralized setting we present a $(4.597+O(\varepsilon))$-approximation algorithm with summary size $O( \frac{k+d}{\varepsilon^2}\log \frac{k}{\varepsilon})$ that is improved to a $(3.582+O(\varepsilon))$-approximation with $O(k + \frac{d}{\varepsilon^2}\log \frac{k}{\varepsilon})$ summary size when the objective is monotone. In the streaming setting we provide a $(9.435 + O(\varepsilon))$-approximation algorithm with summary size and memory $O(k + \frac{d}{\varepsilon^2}\log \frac{k}{\varepsilon})$; the approximation factor is then improved to $(5.582+O(\varepsilon))$ in the monotone case.

Near-Optimal Correlation Clustering with Privacy

Correlation clustering is a central problem in unsupervised learning, with applications spanning community detection, duplicate detection, automated labelling and many more. In the correlation clustering problem one receives as input a set of nodes and for each node a list of co-clustering preferences, and the goal is to output a clustering that minimizes the disagreement with the specified nodes' preferences. In this paper, we introduce a simple and computationally efficient algorithm for the correlation clustering problem with provable privacy guarantees. Our approximation guarantees are stronger than those shown in prior work and are optimal up to logarithmic factors.

Deletion Robust Submodular Maximization over Matroids

Maximizing a monotone submodular function is a fundamental task in machine learning. In this paper, we study the deletion robust version of the problem under the classic matroids constraint. Here the goal is to extract a small size summary of the dataset that contains a high value independent set even after an adversary deleted some elements. We present constant-factor approximation algorithms, whose space complexity depends on the rank $k$ of the matroid and the number $d$ of deleted elements. In the centralized setting we present a $(3.582+O(\varepsilon))$-approximation algorithm with summary size $O(k + \frac{d \log k}{\varepsilon^2})$. In the streaming setting we provide a $(5.582+O(\varepsilon))$-approximation algorithm with summary size and memory $O(k + \frac{d \log k}{\varepsilon^2})$. We complement our theoretical results with an in-depth experimental analysis showing the effectiveness of our algorithms on real-world datasets.

Correlation Clustering in Constant Many Parallel Rounds

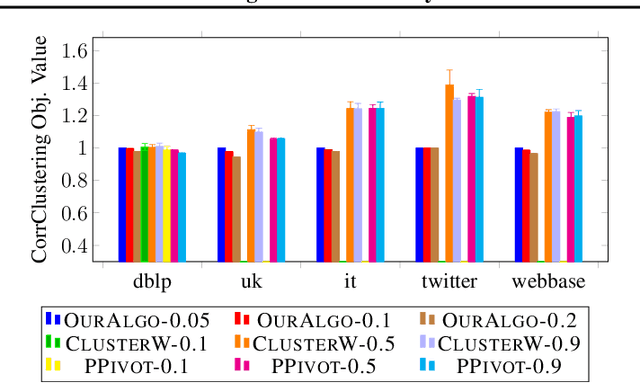
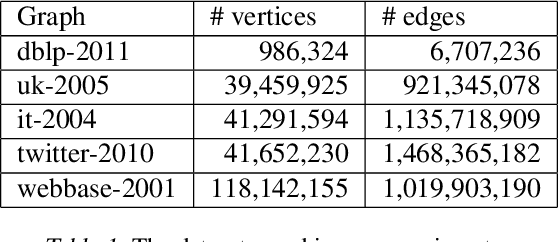
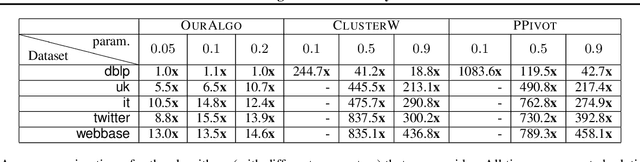
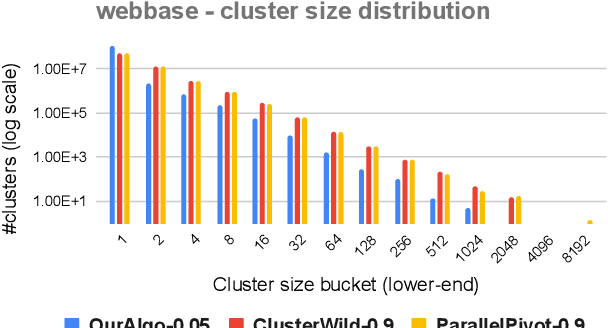
Correlation clustering is a central topic in unsupervised learning, with many applications in ML and data mining. In correlation clustering, one receives as input a signed graph and the goal is to partition it to minimize the number of disagreements. In this work we propose a massively parallel computation (MPC) algorithm for this problem that is considerably faster than prior work. In particular, our algorithm uses machines with memory sublinear in the number of nodes in the graph and returns a constant approximation while running only for a constant number of rounds. To the best of our knowledge, our algorithm is the first that can provably approximate a clustering problem on graphs using only a constant number of MPC rounds in the sublinear memory regime. We complement our analysis with an experimental analysis of our techniques.

Streaming Belief Propagation for Community Detection

The community detection problem requires to cluster the nodes of a network into a small number of well-connected "communities". There has been substantial recent progress in characterizing the fundamental statistical limits of community detection under simple stochastic block models. However, in real-world applications, the network structure is typically dynamic, with nodes that join over time. In this setting, we would like a detection algorithm to perform only a limited number of updates at each node arrival. While standard voting approaches satisfy this constraint, it is unclear whether they exploit the network information optimally. We introduce a simple model for networks growing over time which we refer to as streaming stochastic block model (StSBM). Within this model, we prove that voting algorithms have fundamental limitations. We also develop a streaming belief-propagation (StreamBP) approach, for which we prove optimality in certain regimes. We validate our theoretical findings on synthetic and real data.

Fast and Accurate $k$-means++ via Rejection Sampling

$k$-means++ \cite{arthur2007k} is a widely used clustering algorithm that is easy to implement, has nice theoretical guarantees and strong empirical performance. Despite its wide adoption, $k$-means++ sometimes suffers from being slow on large data-sets so a natural question has been to obtain more efficient algorithms with similar guarantees. In this paper, we present a near linear time algorithm for $k$-means++ seeding. Interestingly our algorithm obtains the same theoretical guarantees as $k$-means++ and significantly improves earlier results on fast $k$-means++ seeding. Moreover, we show empirically that our algorithm is significantly faster than $k$-means++ and obtains solutions of equivalent quality.