Nearly Tight Regret Bounds for Profit Maximization in Bilateral Trade

Bilateral trade models the task of intermediating between two strategic agents, a seller and a buyer, willing to trade a good for which they hold private valuations. We study this problem from the perspective of a broker, in a regret minimization framework. At each time step, a new seller and buyer arrive, and the broker has to propose a mechanism that is incentive-compatible and individually rational, with the goal of maximizing profit. We propose a learning algorithm that guarantees a nearly tight $\tilde{O}(\sqrt{T})$ regret in the stochastic setting when seller and buyer valuations are drawn i.i.d. from a fixed and possibly correlated unknown distribution. We further show that it is impossible to achieve sublinear regret in the non-stationary scenario where valuations are generated upfront by an adversary. Our ambitious benchmark for these results is the best incentive-compatible and individually rational mechanism. This separates us from previous works on efficiency maximization in bilateral trade, where the benchmark is a single number: the best fixed price in hindsight. A particular challenge we face is that uniform convergence for all mechanisms' profits is impossible. We overcome this difficulty via a careful chaining analysis that proves convergence for a provably near-optimal mechanism at (essentially) optimal rate. We further showcase the broader applicability of our techniques by providing nearly optimal results for the joint ads problem.

The Cost of Consistency: Submodular Maximization with Constant Recourse

In this work, we study online submodular maximization, and how the requirement of maintaining a stable solution impacts the approximation. In particular, we seek bounds on the best-possible approximation ratio that is attainable when the algorithm is allowed to make at most a constant number of updates per step. We show a tight information-theoretic bound of $\tfrac{2}{3}$ for general monotone submodular functions, and an improved (also tight) bound of $\tfrac{3}{4}$ for coverage functions. Since both these bounds are attained by non poly-time algorithms, we also give a poly-time randomized algorithm that achieves a $0.51$-approximation. Combined with an information-theoretic hardness of $\tfrac{1}{2}$ for deterministic algorithms from prior work, our work thus shows a separation between deterministic and randomized algorithms, both information theoretically and for poly-time algorithms.

Online Combinatorial Allocations and Auctions with Few Samples

In online combinatorial allocations/auctions, n bidders sequentially arrive, each with a combinatorial valuation (such as submodular/XOS) over subsets of m indivisible items. The aim is to immediately allocate a subset of the remaining items to maximize the total welfare, defined as the sum of bidder valuations. A long line of work has studied this problem when the bidder valuations come from known independent distributions. In particular, for submodular/XOS valuations, we know 2-competitive algorithms/mechanisms that set a fixed price for each item and the arriving bidders take their favorite subset of the remaining items given these prices. However, these algorithms traditionally presume the availability of the underlying distributions as part of the input to the algorithm. Contrary to this assumption, practical scenarios often require the learning of distributions, a task complicated by limited sample availability. This paper investigates the feasibility of achieving O(1)-competitive algorithms under the realistic constraint of having access to only a limited number of samples from the underlying bidder distributions. Our first main contribution shows that a mere single sample from each bidder distribution is sufficient to yield an O(1)-competitive algorithm for submodular/XOS valuations. This result leverages a novel extension of the secretary-style analysis, employing the sample to have the algorithm compete against itself. Although online, this first approach does not provide an online truthful mechanism. Our second main contribution shows that a polynomial number of samples suffices to yield a $(2+\epsilon)$-competitive online truthful mechanism for submodular/XOS valuations and any constant $\epsilon>0$. This result is based on a generalization of the median-based algorithm for the single-item prophet inequality problem to combinatorial settings with multiple items.

Selling Joint Ads: A Regret Minimization Perspective

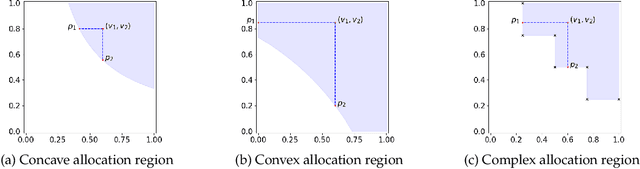
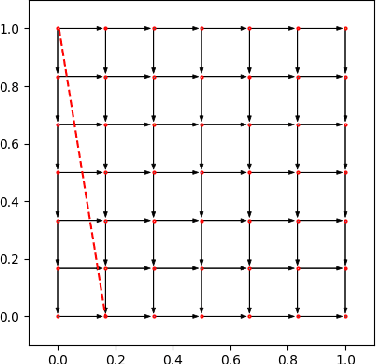
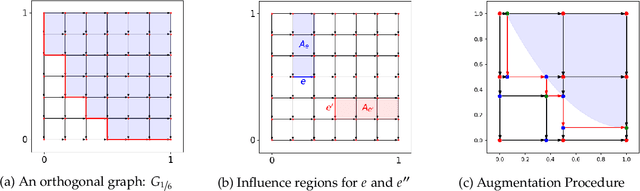
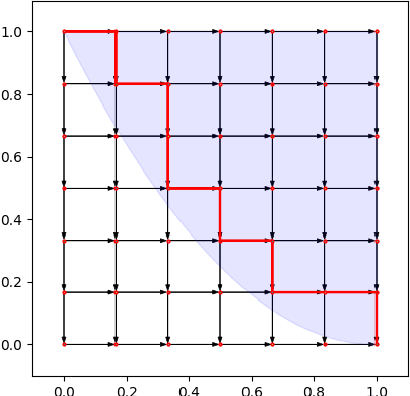
Motivated by online retail, we consider the problem of selling one item (e.g., an ad slot) to two non-excludable buyers (say, a merchant and a brand). This problem captures, for example, situations where a merchant and a brand cooperatively bid in an auction to advertise a product, and both benefit from the ad being shown. A mechanism collects bids from the two and decides whether to allocate and which payments the two parties should make. This gives rise to intricate incentive compatibility constraints, e.g., on how to split payments between the two parties. We approach the problem of finding a revenue-maximizing incentive-compatible mechanism from an online learning perspective; this poses significant technical challenges. First, the action space (the class of all possible mechanisms) is huge; second, the function that maps mechanisms to revenue is highly irregular, ruling out standard discretization-based approaches. In the stochastic setting, we design an efficient learning algorithm achieving a regret bound of $O(T^{3/4})$. Our approach is based on an adaptive discretization scheme of the space of mechanisms, as any non-adaptive discretization fails to achieve sublinear regret. In the adversarial setting, we exploit the non-Lipschitzness of the problem to prove a strong negative result, namely that no learning algorithm can achieve more than half of the revenue of the best fixed mechanism in hindsight. We then consider the $\sigma$-smooth adversary; we construct an efficient learning algorithm that achieves a regret bound of $O(T^{2/3})$ and builds on a succinct encoding of exponentially many experts. Finally, we prove that no learning algorithm can achieve less than $\Omega(\sqrt T)$ regret in both the stochastic and the smooth setting, thus narrowing the range where the minimax regret rates for these two problems lie.

Principal-Agent Reinforcement Learning

Contracts are the economic framework which allows a principal to delegate a task to an agent -- despite misaligned interests, and even without directly observing the agent's actions. In many modern reinforcement learning settings, self-interested agents learn to perform a multi-stage task delegated to them by a principal. We explore the significant potential of utilizing contracts to incentivize the agents. We model the delegated task as an MDP, and study a stochastic game between the principal and agent where the principal learns what contracts to use, and the agent learns an MDP policy in response. We present a learning-based algorithm for optimizing the principal's contracts, which provably converges to the subgame-perfect equilibrium of the principal-agent game. A deep RL implementation allows us to apply our method to very large MDPs with unknown transition dynamics. We extend our approach to multiple agents, and demonstrate its relevance to resolving a canonical sequential social dilemma with minimal intervention to agent rewards.

Consistent Submodular Maximization

Maximizing monotone submodular functions under cardinality constraints is a classic optimization task with several applications in data mining and machine learning. In this paper we study this problem in a dynamic environment with consistency constraints: elements arrive in a streaming fashion and the goal is maintaining a constant approximation to the optimal solution while having a stable solution (i.e., the number of changes between two consecutive solutions is bounded). We provide algorithms in this setting with different trade-offs between consistency and approximation quality. We also complement our theoretical results with an experimental analysis showing the effectiveness of our algorithms in real-world instances.

Deep Contract Design via Discontinuous Piecewise Affine Neural Networks

Contract design involves a principal who establishes contractual agreements about payments for outcomes that arise from the actions of an agent. In this paper, we initiate the study of deep learning for the automated design of optimal contracts. We formulate this as an offline learning problem, where a deep network is used to represent the principal's expected utility as a function of the design of a contract. We introduce a novel representation: the Discontinuous ReLU (DeLU) network, which models the principal's utility as a discontinuous piecewise affine function where each piece corresponds to the agent taking a particular action. DeLU networks implicitly learn closed-form expressions for the incentive compatibility constraints of the agent and the utility maximization objective of the principal, and support parallel inference on each piece through linear programming or interior-point methods that solve for optimal contracts. We provide empirical results that demonstrate success in approximating the principal's utility function with a small number of training samples and scaling to find approximately optimal contracts on problems with a large number of actions and outcomes.

Fully Dynamic Submodular Maximization over Matroids

Maximizing monotone submodular functions under a matroid constraint is a classic algorithmic problem with multiple applications in data mining and machine learning. We study this classic problem in the fully dynamic setting, where elements can be both inserted and deleted in real-time. Our main result is a randomized algorithm that maintains an efficient data structure with an $\tilde{O}(k^2)$ amortized update time (in the number of additions and deletions) and yields a $4$-approximate solution, where $k$ is the rank of the matroid.

Deletion Robust Non-Monotone Submodular Maximization over Matroids

Maximizing a submodular function is a fundamental task in machine learning and in this paper we study the deletion robust version of the problem under the classic matroids constraint. Here the goal is to extract a small size summary of the dataset that contains a high value independent set even after an adversary deleted some elements. We present constant-factor approximation algorithms, whose space complexity depends on the rank $k$ of the matroid and the number $d$ of deleted elements. In the centralized setting we present a $(4.597+O(\varepsilon))$-approximation algorithm with summary size $O( \frac{k+d}{\varepsilon^2}\log \frac{k}{\varepsilon})$ that is improved to a $(3.582+O(\varepsilon))$-approximation with $O(k + \frac{d}{\varepsilon^2}\log \frac{k}{\varepsilon})$ summary size when the objective is monotone. In the streaming setting we provide a $(9.435 + O(\varepsilon))$-approximation algorithm with summary size and memory $O(k + \frac{d}{\varepsilon^2}\log \frac{k}{\varepsilon})$; the approximation factor is then improved to $(5.582+O(\varepsilon))$ in the monotone case.

Deletion Robust Submodular Maximization over Matroids

Maximizing a monotone submodular function is a fundamental task in machine learning. In this paper, we study the deletion robust version of the problem under the classic matroids constraint. Here the goal is to extract a small size summary of the dataset that contains a high value independent set even after an adversary deleted some elements. We present constant-factor approximation algorithms, whose space complexity depends on the rank $k$ of the matroid and the number $d$ of deleted elements. In the centralized setting we present a $(3.582+O(\varepsilon))$-approximation algorithm with summary size $O(k + \frac{d \log k}{\varepsilon^2})$. In the streaming setting we provide a $(5.582+O(\varepsilon))$-approximation algorithm with summary size and memory $O(k + \frac{d \log k}{\varepsilon^2})$. We complement our theoretical results with an in-depth experimental analysis showing the effectiveness of our algorithms on real-world datasets.