Randomized Truthful Auctions with Learning Agents

We study a setting where agents use no-regret learning algorithms to participate in repeated auctions. \citet{kolumbus2022auctions} showed, rather surprisingly, that when bidders participate in second-price auctions using no-regret bidding algorithms, no matter how large the number of interactions $T$ is, the runner-up bidder may not converge to bidding truthfully. Our first result shows that this holds for \emph{general deterministic} truthful auctions. We also show that the ratio of the learning rates of the bidders can \emph{qualitatively} affect the convergence of the bidders. Next, we consider the problem of revenue maximization in this environment. In the setting with fully rational bidders, \citet{myerson1981optimal} showed that revenue can be maximized by using a second-price auction with reserves.We show that, in stark contrast, in our setting with learning bidders, \emph{randomized} auctions can have strictly better revenue guarantees than second-price auctions with reserves, when $T$ is large enough. Finally, we study revenue maximization in the non-asymptotic regime. We define a notion of {\em auctioneer regret} comparing the revenue generated to the revenue of a second price auction with truthful bids. When the auctioneer has to use the same auction throughout the interaction, we show an (almost) tight regret bound of $\smash{\widetilde \Theta(T^{3/4})}.$ If the auctioneer can change auctions during the interaction, but in a way that is oblivious to the bids, we show an (almost) tight bound of $\smash{\widetilde \Theta(\sqrt{T})}.$

Selling Joint Ads: A Regret Minimization Perspective

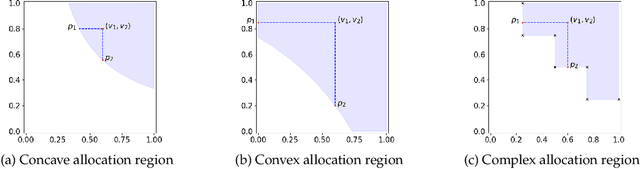
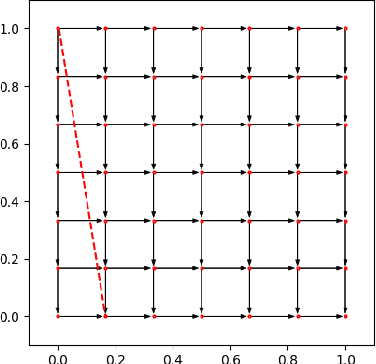
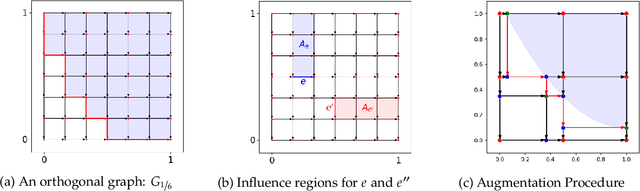
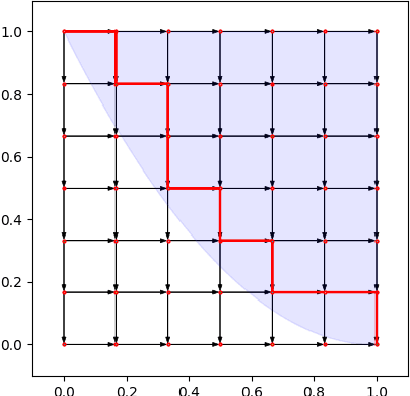
Motivated by online retail, we consider the problem of selling one item (e.g., an ad slot) to two non-excludable buyers (say, a merchant and a brand). This problem captures, for example, situations where a merchant and a brand cooperatively bid in an auction to advertise a product, and both benefit from the ad being shown. A mechanism collects bids from the two and decides whether to allocate and which payments the two parties should make. This gives rise to intricate incentive compatibility constraints, e.g., on how to split payments between the two parties. We approach the problem of finding a revenue-maximizing incentive-compatible mechanism from an online learning perspective; this poses significant technical challenges. First, the action space (the class of all possible mechanisms) is huge; second, the function that maps mechanisms to revenue is highly irregular, ruling out standard discretization-based approaches. In the stochastic setting, we design an efficient learning algorithm achieving a regret bound of $O(T^{3/4})$. Our approach is based on an adaptive discretization scheme of the space of mechanisms, as any non-adaptive discretization fails to achieve sublinear regret. In the adversarial setting, we exploit the non-Lipschitzness of the problem to prove a strong negative result, namely that no learning algorithm can achieve more than half of the revenue of the best fixed mechanism in hindsight. We then consider the $\sigma$-smooth adversary; we construct an efficient learning algorithm that achieves a regret bound of $O(T^{2/3})$ and builds on a succinct encoding of exponentially many experts. Finally, we prove that no learning algorithm can achieve less than $\Omega(\sqrt T)$ regret in both the stochastic and the smooth setting, thus narrowing the range where the minimax regret rates for these two problems lie.

No-Regret Algorithms in non-Truthful Auctions with Budget and ROI Constraints

Advertisers increasingly use automated bidding to optimize their ad campaigns on online advertising platforms. Autobidding optimizes an advertiser's objective subject to various constraints, e.g. average ROI and budget constraints. In this paper, we study the problem of designing online autobidding algorithms to optimize value subject to ROI and budget constraints when the platform is running any mixture of first and second price auction. We consider the following stochastic setting: There is an item for sale in each of $T$ rounds. In each round, buyers submit bids and an auction is run to sell the item. We focus on one buyer, possibly with budget and ROI constraints. We assume that the buyer's value and the highest competing bid are drawn i.i.d. from some unknown (joint) distribution in each round. We design a low-regret bidding algorithm that satisfies the buyer's constraints. Our benchmark is the objective value achievable by the best possible Lipschitz function that maps values to bids, which is rich enough to best respond to many different correlation structures between value and highest competing bid. Our main result is an algorithm with full information feedback that guarantees a near-optimal $\tilde O(\sqrt T)$ regret with respect to the best Lipschitz function. Our result applies to a wide range of auctions, most notably any mixture of first and second price auctions (price is a convex combination of the first and second price). In addition, our result holds for both value-maximizing buyers and quasi-linear utility-maximizing buyers. We also study the bandit setting, where we show an $\Omega(T^{2/3})$ lower bound on the regret for first-price auctions, showing a large disparity between the full information and bandit settings. We also design an algorithm with $\tilde O(T^{3/4})$ regret, when the value distribution is known and is independent of the highest competing bid.