Learning in Budgeted Auctions with Spacing Objectives

In many repeated auction settings, participants care not only about how frequently they win but also how their winnings are distributed over time. This problem arises in various practical domains where avoiding congested demand is crucial, such as online retail sales and compute services, as well as in advertising campaigns that require sustained visibility over time. We introduce a simple model of this phenomenon, modeling it as a budgeted auction where the value of a win is a concave function of the time since the last win. This implies that for a given number of wins, even spacing over time is optimal. We also extend our model and results to the case when not all wins result in "conversions" (realization of actual gains), and the probability of conversion depends on a context. The goal is to maximize and evenly space conversions rather than just wins. We study the optimal policies for this setting in second-price auctions and offer learning algorithms for the bidders that achieve low regret against the optimal bidding policy in a Bayesian online setting. Our main result is a computationally efficient online learning algorithm that achieves $\tilde O(\sqrt T)$ regret. We achieve this by showing that an infinite-horizon Markov decision process (MDP) with the budget constraint in expectation is essentially equivalent to our problem, even when limiting that MDP to a very small number of states. The algorithm achieves low regret by learning a bidding policy that chooses bids as a function of the context and the system's state, which will be the time elapsed since the last win (or conversion). We show that state-independent strategies incur linear regret even without uncertainty of conversions. We complement this by showing that there are state-independent strategies that, while still having linear regret, achieve a $(1-\frac 1 e)$ approximation to the optimal reward.

No-Regret Algorithms in non-Truthful Auctions with Budget and ROI Constraints

Advertisers increasingly use automated bidding to optimize their ad campaigns on online advertising platforms. Autobidding optimizes an advertiser's objective subject to various constraints, e.g. average ROI and budget constraints. In this paper, we study the problem of designing online autobidding algorithms to optimize value subject to ROI and budget constraints when the platform is running any mixture of first and second price auction. We consider the following stochastic setting: There is an item for sale in each of $T$ rounds. In each round, buyers submit bids and an auction is run to sell the item. We focus on one buyer, possibly with budget and ROI constraints. We assume that the buyer's value and the highest competing bid are drawn i.i.d. from some unknown (joint) distribution in each round. We design a low-regret bidding algorithm that satisfies the buyer's constraints. Our benchmark is the objective value achievable by the best possible Lipschitz function that maps values to bids, which is rich enough to best respond to many different correlation structures between value and highest competing bid. Our main result is an algorithm with full information feedback that guarantees a near-optimal $\tilde O(\sqrt T)$ regret with respect to the best Lipschitz function. Our result applies to a wide range of auctions, most notably any mixture of first and second price auctions (price is a convex combination of the first and second price). In addition, our result holds for both value-maximizing buyers and quasi-linear utility-maximizing buyers. We also study the bandit setting, where we show an $\Omega(T^{2/3})$ lower bound on the regret for first-price auctions, showing a large disparity between the full information and bandit settings. We also design an algorithm with $\tilde O(T^{3/4})$ regret, when the value distribution is known and is independent of the highest competing bid.

Approximately Stationary Bandits with Knapsacks

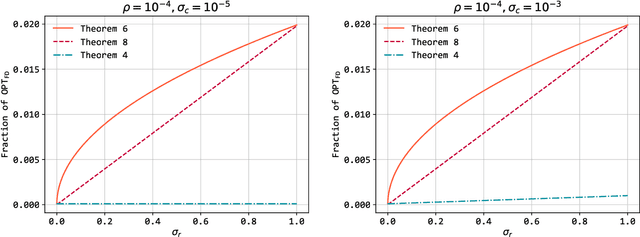
Bandits with Knapsacks (BwK), the generalization of the Multi-Armed Bandits under budget constraints, has received a lot of attention in recent years. It has numerous applications, including dynamic pricing, repeated auctions, etc. Previous work has focused on one of the two extremes: Stochastic BwK where the rewards and consumptions of the resources each round are sampled from an i.i.d. distribution, and Adversarial BwK where these values are picked by an adversary. Achievable guarantees in the two cases exhibit a massive gap: No-regret learning is achievable in Stochastic BwK, but in Adversarial BwK, only competitive ratio style guarantees are achievable, where the competitive ratio depends on the budget. What makes this gap so vast is that in Adversarial BwK the guarantees get worse in the typical case when the budget is more binding. While ``best-of-both-worlds'' type algorithms are known (algorithms that provide the best achievable guarantee in both extreme cases), their guarantees degrade to the adversarial case as soon as the environment is not fully stochastic. Our work aims to bridge this gap, offering guarantees for a workload that is not exactly stochastic but is also not worst-case. We define a condition, Approximately Stationary BwK, that parameterizes how close to stochastic or adversarial an instance is. Based on these parameters, we explore what is the best competitive ratio attainable in BwK. We explore two algorithms that are oblivious to the values of the parameters but guarantee competitive ratios that smoothly transition between the best possible guarantees in the two extreme cases, depending on the values of the parameters. Our guarantees offer great improvement over the adversarial guarantee, especially when the available budget is small. We also prove bounds on the achievable guarantee, showing that our results are approximately tight when the budget is small.

Optimizing Vessel Trajectory Compression

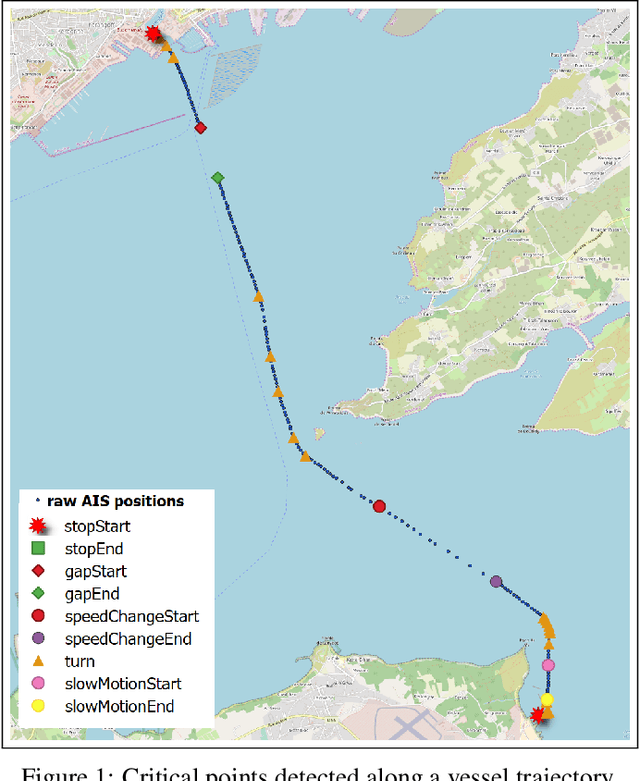
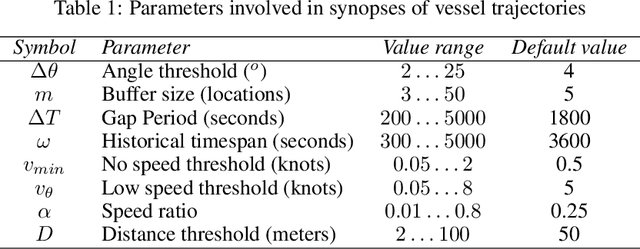
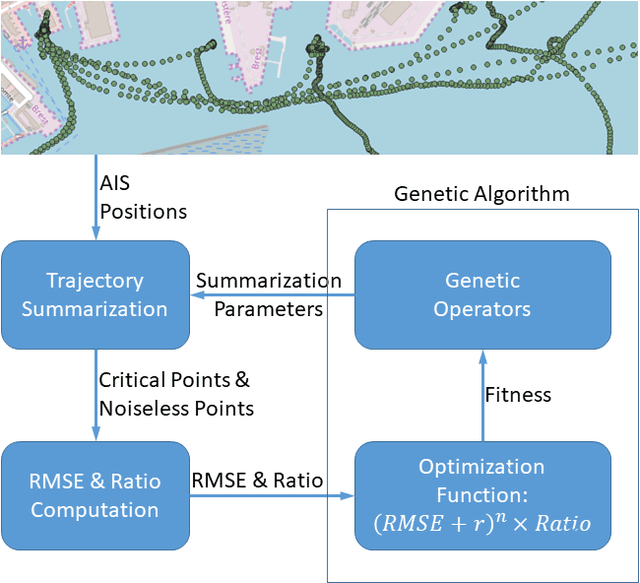
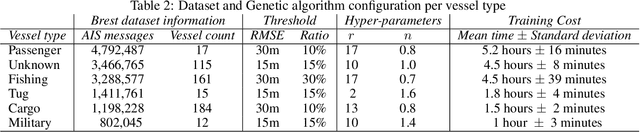
In previous work we introduced a trajectory detection module that can provide summarized representations of vessel trajectories by consuming AIS positional messages online. This methodology can provide reliable trajectory synopses with little deviations from the original course by discarding at least 70% of the raw data as redundant. However, such trajectory compression is very sensitive to parametrization. In this paper, our goal is to fine-tune the selection of these parameter values. We take into account the type of each vessel in order to provide a suitable configuration that can yield improved trajectory synopses, both in terms of approximation error and compression ratio. Furthermore, we employ a genetic algorithm converging to a suitable configuration per vessel type. Our tests against a publicly available AIS dataset have shown that compression efficiency is comparable or even better than the one with default parametrization without resorting to a laborious data inspection.