Mingfei Zhao
No-Regret Algorithms in non-Truthful Auctions with Budget and ROI Constraints
Apr 15, 2024Abstract:Advertisers increasingly use automated bidding to optimize their ad campaigns on online advertising platforms. Autobidding optimizes an advertiser's objective subject to various constraints, e.g. average ROI and budget constraints. In this paper, we study the problem of designing online autobidding algorithms to optimize value subject to ROI and budget constraints when the platform is running any mixture of first and second price auction. We consider the following stochastic setting: There is an item for sale in each of $T$ rounds. In each round, buyers submit bids and an auction is run to sell the item. We focus on one buyer, possibly with budget and ROI constraints. We assume that the buyer's value and the highest competing bid are drawn i.i.d. from some unknown (joint) distribution in each round. We design a low-regret bidding algorithm that satisfies the buyer's constraints. Our benchmark is the objective value achievable by the best possible Lipschitz function that maps values to bids, which is rich enough to best respond to many different correlation structures between value and highest competing bid. Our main result is an algorithm with full information feedback that guarantees a near-optimal $\tilde O(\sqrt T)$ regret with respect to the best Lipschitz function. Our result applies to a wide range of auctions, most notably any mixture of first and second price auctions (price is a convex combination of the first and second price). In addition, our result holds for both value-maximizing buyers and quasi-linear utility-maximizing buyers. We also study the bandit setting, where we show an $\Omega(T^{2/3})$ lower bound on the regret for first-price auctions, showing a large disparity between the full information and bandit settings. We also design an algorithm with $\tilde O(T^{3/4})$ regret, when the value distribution is known and is independent of the highest competing bid.
Robust Influence Maximization
Jun 12, 2016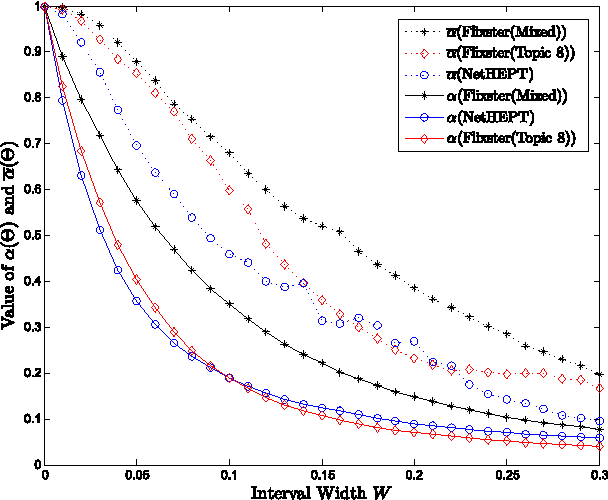



Abstract:In this paper, we address the important issue of uncertainty in the edge influence probability estimates for the well studied influence maximization problem --- the task of finding $k$ seed nodes in a social network to maximize the influence spread. We propose the problem of robust influence maximization, which maximizes the worst-case ratio between the influence spread of the chosen seed set and the optimal seed set, given the uncertainty of the parameter input. We design an algorithm that solves this problem with a solution-dependent bound. We further study uniform sampling and adaptive sampling methods to effectively reduce the uncertainty on parameters and improve the robustness of the influence maximization task. Our empirical results show that parameter uncertainty may greatly affect influence maximization performance and prior studies that learned influence probabilities could lead to poor performance in robust influence maximization due to relatively large uncertainty in parameter estimates, and information cascade based adaptive sampling method may be an effective way to improve the robustness of influence maximization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge