Approximately Stationary Bandits with Knapsacks

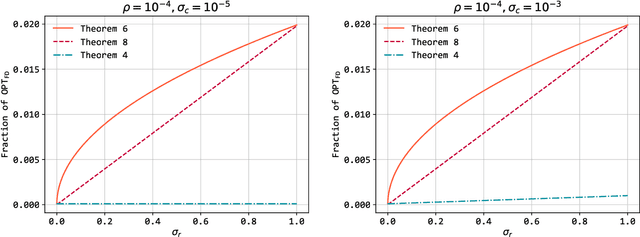
Bandits with Knapsacks (BwK), the generalization of the Multi-Armed Bandits under budget constraints, has received a lot of attention in recent years. It has numerous applications, including dynamic pricing, repeated auctions, etc. Previous work has focused on one of the two extremes: Stochastic BwK where the rewards and consumptions of the resources each round are sampled from an i.i.d. distribution, and Adversarial BwK where these values are picked by an adversary. Achievable guarantees in the two cases exhibit a massive gap: No-regret learning is achievable in Stochastic BwK, but in Adversarial BwK, only competitive ratio style guarantees are achievable, where the competitive ratio depends on the budget. What makes this gap so vast is that in Adversarial BwK the guarantees get worse in the typical case when the budget is more binding. While ``best-of-both-worlds'' type algorithms are known (algorithms that provide the best achievable guarantee in both extreme cases), their guarantees degrade to the adversarial case as soon as the environment is not fully stochastic. Our work aims to bridge this gap, offering guarantees for a workload that is not exactly stochastic but is also not worst-case. We define a condition, Approximately Stationary BwK, that parameterizes how close to stochastic or adversarial an instance is. Based on these parameters, we explore what is the best competitive ratio attainable in BwK. We explore two algorithms that are oblivious to the values of the parameters but guarantee competitive ratios that smoothly transition between the best possible guarantees in the two extreme cases, depending on the values of the parameters. Our guarantees offer great improvement over the adversarial guarantee, especially when the available budget is small. We also prove bounds on the achievable guarantee, showing that our results are approximately tight when the budget is small.