On Agnostic PAC Learning in the Small Error Regime

Binary classification in the classic PAC model exhibits a curious phenomenon: Empirical Risk Minimization (ERM) learners are suboptimal in the realizable case yet optimal in the agnostic case. Roughly speaking, this owes itself to the fact that non-realizable distributions $\mathcal{D}$ are simply more difficult to learn than realizable distributions -- even when one discounts a learner's error by $\mathrm{err}(h^*_{\mathcal{D}})$, the error of the best hypothesis in $\mathcal{H}$ for $\mathcal{D}$. Thus, optimal agnostic learners are permitted to incur excess error on (easier-to-learn) distributions $\mathcal{D}$ for which $\tau = \mathrm{err}(h^*_{\mathcal{D}})$ is small. Recent work of Hanneke, Larsen, and Zhivotovskiy (FOCS `24) addresses this shortcoming by including $\tau$ itself as a parameter in the agnostic error term. In this more fine-grained model, they demonstrate tightness of the error lower bound $\tau + \Omega \left(\sqrt{\frac{\tau (d + \log(1 / \delta))}{m}} + \frac{d + \log(1 / \delta)}{m} \right)$ in a regime where $\tau > d/m$, and leave open the question of whether there may be a higher lower bound when $\tau \approx d/m$, with $d$ denoting $\mathrm{VC}(\mathcal{H})$. In this work, we resolve this question by exhibiting a learner which achieves error $c \cdot \tau + O \left(\sqrt{\frac{\tau (d + \log(1 / \delta))}{m}} + \frac{d + \log(1 / \delta)}{m} \right)$ for a constant $c \leq 2.1$, thus matching the lower bound when $\tau \approx d/m$. Further, our learner is computationally efficient and is based upon careful aggregations of ERM classifiers, making progress on two other questions of Hanneke, Larsen, and Zhivotovskiy (FOCS `24). We leave open the interesting question of whether our approach can be refined to lower the constant from 2.1 to 1, which would completely settle the complexity of agnostic learning.

Characterizations of Language Generation With Breadth

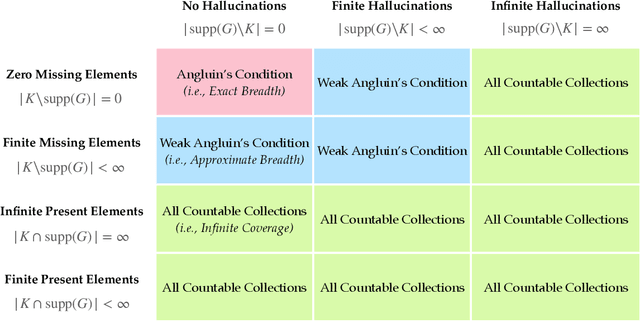
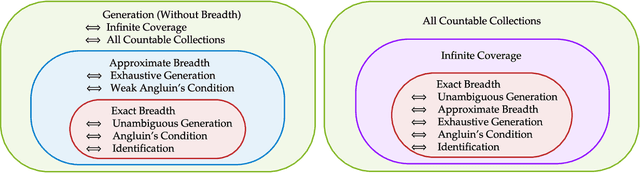
We study language generation in the limit, introduced by Kleinberg and Mullainathan [KM24], building on classical works of Gold [Gol67] and Angluin [Ang79]. [KM24] proposed an algorithm that generates strings from any countable language collection in the limit. While their algorithm eventually outputs strings from the target language $K$, it sacrifices breadth, i.e., the ability to generate all strings in $K$. A key open question in [KM24] is whether this trade-off between consistency and breadth is inherrent. Recent works proposed different notions of consistent generation with breadth. Kalavasis, Mehrotra, and Velegkas [KVM24] introduced three definitions: generation with exact breadth, approximate breadth, and unambiguous generation. Concurrently and independently, Charikar and Pabbaraju [CP24a] proposed exhaustive generation. Both works examined when generation with these notions of breadth is possible. Building on [CP24a, KVM24], we fully characterize language generation for these notions and their natural combinations. For exact breadth, we provide an unconditional lower bound, removing a technical condition from [KVM24] and extending the result of [CP24a] that holds for specific collections of languages. We show that generation with exact breadth is characterized by Angluin's condition for identification. We further introduce a weaker version of Angluin's condition that tightly characterizes both approximate breadth and exhaustive generation, proving their equivalence. Additionally, we show that unambiguous generation is also characterized by Angluin's condition as a special case of a broader result. Finally, we strengthen [KVM24] by giving unconditional lower bounds for stable generators, showing that Angluin's condition characterizes the previous breadth notions for stable generators. This shows a separation between stable and unstable generation with approximate breadth.

Procurement Auctions via Approximately Optimal Submodular Optimization

We study procurement auctions, where an auctioneer seeks to acquire services from strategic sellers with private costs. The quality of services is measured by a submodular function known to the auctioneer. Our goal is to design computationally efficient procurement auctions that (approximately) maximize the difference between the quality of the acquired services and the total cost of the sellers, while ensuring incentive compatibility (IC), individual rationality (IR) for sellers, and non-negative surplus (NAS) for the auctioneer. Our contributions are twofold: (i) we provide an improved analysis of existing algorithms for non-positive submodular function maximization, and (ii) we design efficient frameworks that transform submodular optimization algorithms into mechanisms that are IC, IR, NAS, and approximation-preserving. These frameworks apply to both the offline setting, where all sellers' bids and services are available simultaneously, and the online setting, where sellers arrive in an adversarial order, requiring the auctioneer to make irrevocable decisions. We also explore whether state-of-the-art submodular optimization algorithms can be converted into descending auctions in adversarial settings, where the schedule of descending prices is determined by an adversary. We show that a submodular optimization algorithm satisfying bi-criteria $(1/2, 1)$-approximation in welfare can be effectively adapted to a descending auction. Additionally, we establish a connection between descending auctions and online submodular optimization. Finally, we demonstrate the practical applications of our frameworks by instantiating them with state-of-the-art submodular optimization algorithms and empirically comparing their welfare performance on publicly available datasets with thousands of sellers.

On the Limits of Language Generation: Trade-Offs Between Hallucination and Mode Collapse

Specifying all desirable properties of a language model is challenging, but certain requirements seem essential. Given samples from an unknown language, the trained model should produce valid strings not seen in training and be expressive enough to capture the language's full richness. Otherwise, outputting invalid strings constitutes "hallucination," and failing to capture the full range leads to "mode collapse." We ask if a language model can meet both requirements. We investigate this within a statistical language generation setting building on Gold and Angluin. Here, the model receives random samples from a distribution over an unknown language K, which belongs to a possibly infinite collection of languages. The goal is to generate unseen strings from K. We say the model generates from K with consistency and breadth if, as training size increases, its output converges to all unseen strings in K. Kleinberg and Mullainathan [KM24] asked if consistency and breadth in language generation are possible. We answer this negatively: for a large class of language models, including next-token prediction models, this is impossible for most collections of candidate languages. This contrasts with [KM24]'s result, showing consistent generation without breadth is possible for any countable collection of languages. Our finding highlights that generation with breadth fundamentally differs from generation without breadth. As a byproduct, we establish near-tight bounds on the number of samples needed for generation with or without breadth. Finally, our results offer hope: consistent generation with breadth is achievable for any countable collection of languages when negative examples (strings outside K) are available alongside positive ones. This suggests that post-training feedback, which encodes negative examples, can be crucial in reducing hallucinations while limiting mode collapse.

Randomized Truthful Auctions with Learning Agents

We study a setting where agents use no-regret learning algorithms to participate in repeated auctions. \citet{kolumbus2022auctions} showed, rather surprisingly, that when bidders participate in second-price auctions using no-regret bidding algorithms, no matter how large the number of interactions $T$ is, the runner-up bidder may not converge to bidding truthfully. Our first result shows that this holds for \emph{general deterministic} truthful auctions. We also show that the ratio of the learning rates of the bidders can \emph{qualitatively} affect the convergence of the bidders. Next, we consider the problem of revenue maximization in this environment. In the setting with fully rational bidders, \citet{myerson1981optimal} showed that revenue can be maximized by using a second-price auction with reserves.We show that, in stark contrast, in our setting with learning bidders, \emph{randomized} auctions can have strictly better revenue guarantees than second-price auctions with reserves, when $T$ is large enough. Finally, we study revenue maximization in the non-asymptotic regime. We define a notion of {\em auctioneer regret} comparing the revenue generated to the revenue of a second price auction with truthful bids. When the auctioneer has to use the same auction throughout the interaction, we show an (almost) tight regret bound of $\smash{\widetilde \Theta(T^{3/4})}.$ If the auctioneer can change auctions during the interaction, but in a way that is oblivious to the bids, we show an (almost) tight bound of $\smash{\widetilde \Theta(\sqrt{T})}.$

Understanding Aggregations of Proper Learners in Multiclass Classification

Multiclass learnability is known to exhibit a properness barrier: there are learnable classes which cannot be learned by any proper learner. Binary classification faces no such barrier for learnability, but a similar one for optimal learning, which can in general only be achieved by improper learners. Fortunately, recent advances in binary classification have demonstrated that this requirement can be satisfied using aggregations of proper learners, some of which are strikingly simple. This raises a natural question: to what extent can simple aggregations of proper learners overcome the properness barrier in multiclass classification? We give a positive answer to this question for classes which have finite Graph dimension, $d_G$. Namely, we demonstrate that the optimal binary learners of Hanneke, Larsen, and Aden-Ali et al. (appropriately generalized to the multiclass setting) achieve sample complexity $O\left(\frac{d_G + \ln(1 / \delta)}{\epsilon}\right)$. This forms a strict improvement upon the sample complexity of ERM. We complement this with a lower bound demonstrating that for certain classes of Graph dimension $d_G$, majorities of ERM learners require $\Omega \left( \frac{d_G + \ln(1 / \delta)}{\epsilon}\right)$ samples. Furthermore, we show that a single ERM requires $\Omega \left(\frac{d_G \ln(1 / \epsilon) + \ln(1 / \delta)}{\epsilon}\right)$ samples on such classes, exceeding the lower bound of Daniely et al. (2015) by a factor of $\ln(1 / \epsilon)$. For multiclass learning in full generality -- i.e., for classes of finite DS dimension but possibly infinite Graph dimension -- we give a strong refutation to these learning strategies, by exhibiting a learnable class which cannot be learned to constant error by any aggregation of a finite number of proper learners.

Injecting Undetectable Backdoors in Deep Learning and Language Models

As ML models become increasingly complex and integral to high-stakes domains such as finance and healthcare, they also become more susceptible to sophisticated adversarial attacks. We investigate the threat posed by undetectable backdoors in models developed by insidious external expert firms. When such backdoors exist, they allow the designer of the model to sell information to the users on how to carefully perturb the least significant bits of their input to change the classification outcome to a favorable one. We develop a general strategy to plant a backdoor to neural networks while ensuring that even if the model's weights and architecture are accessible, the existence of the backdoor is still undetectable. To achieve this, we utilize techniques from cryptography such as cryptographic signatures and indistinguishability obfuscation. We further introduce the notion of undetectable backdoors to language models and extend our neural network backdoor attacks to such models based on the existence of steganographic functions.

On the Computational Landscape of Replicable Learning

We study computational aspects of algorithmic replicability, a notion of stability introduced by Impagliazzo, Lei, Pitassi, and Sorrell [2022]. Motivated by a recent line of work that established strong statistical connections between replicability and other notions of learnability such as online learning, private learning, and SQ learning, we aim to understand better the computational connections between replicability and these learning paradigms. Our first result shows that there is a concept class that is efficiently replicably PAC learnable, but, under standard cryptographic assumptions, no efficient online learner exists for this class. Subsequently, we design an efficient replicable learner for PAC learning parities when the marginal distribution is far from uniform, making progress on a question posed by Impagliazzo et al. [2022]. To obtain this result, we design a replicable lifting framework inspired by Blanc, Lange, Malik, and Tan [2023] that transforms in a black-box manner efficient replicable PAC learners under the uniform marginal distribution over the Boolean hypercube to replicable PAC learners under any marginal distribution, with sample and time complexity that depends on a certain measure of the complexity of the distribution. Finally, we show that any pure DP learner can be transformed to a replicable one in time polynomial in the accuracy, confidence parameters and exponential in the representation dimension of the underlying hypothesis class.

Replicable Learning of Large-Margin Halfspaces

We provide efficient replicable algorithms for the problem of learning large-margin halfspaces. Our results improve upon the algorithms provided by Impagliazzo, Lei, Pitassi, and Sorrell [STOC, 2022]. We design the first dimension-independent replicable algorithms for this task which runs in polynomial time, is proper, and has strictly improved sample complexity compared to the one achieved by Impagliazzo et al. [2022] with respect to all the relevant parameters. Moreover, our first algorithm has sample complexity that is optimal with respect to the accuracy parameter $\epsilon$. We also design an SGD-based replicable algorithm that, in some parameters' regimes, achieves better sample and time complexity than our first algorithm. Departing from the requirement of polynomial time algorithms, using the DP-to-Replicability reduction of Bun, Gaboardi, Hopkins, Impagliazzo, Lei, Pitassi, Sorrell, and Sivakumar [STOC, 2023], we show how to obtain a replicable algorithm for large-margin halfspaces with improved sample complexity with respect to the margin parameter $\tau$, but running time doubly exponential in $1/\tau^2$ and worse sample complexity dependence on $\epsilon$ than one of our previous algorithms. We then design an improved algorithm with better sample complexity than all three of our previous algorithms and running time exponential in $1/\tau^{2}$.

Optimal Learners for Realizable Regression: PAC Learning and Online Learning

In this work, we aim to characterize the statistical complexity of realizable regression both in the PAC learning setting and the online learning setting. Previous work had established the sufficiency of finiteness of the fat shattering dimension for PAC learnability and the necessity of finiteness of the scaled Natarajan dimension, but little progress had been made towards a more complete characterization since the work of Simon 1997 (SICOMP '97). To this end, we first introduce a minimax instance optimal learner for realizable regression and propose a novel dimension that both qualitatively and quantitatively characterizes which classes of real-valued predictors are learnable. We then identify a combinatorial dimension related to the Graph dimension that characterizes ERM learnability in the realizable setting. Finally, we establish a necessary condition for learnability based on a combinatorial dimension related to the DS dimension, and conjecture that it may also be sufficient in this context. Additionally, in the context of online learning we provide a dimension that characterizes the minimax instance optimal cumulative loss up to a constant factor and design an optimal online learner for realizable regression, thus resolving an open question raised by Daskalakis and Golowich in STOC '22.