Procurement Auctions via Approximately Optimal Submodular Optimization

We study procurement auctions, where an auctioneer seeks to acquire services from strategic sellers with private costs. The quality of services is measured by a submodular function known to the auctioneer. Our goal is to design computationally efficient procurement auctions that (approximately) maximize the difference between the quality of the acquired services and the total cost of the sellers, while ensuring incentive compatibility (IC), individual rationality (IR) for sellers, and non-negative surplus (NAS) for the auctioneer. Our contributions are twofold: (i) we provide an improved analysis of existing algorithms for non-positive submodular function maximization, and (ii) we design efficient frameworks that transform submodular optimization algorithms into mechanisms that are IC, IR, NAS, and approximation-preserving. These frameworks apply to both the offline setting, where all sellers' bids and services are available simultaneously, and the online setting, where sellers arrive in an adversarial order, requiring the auctioneer to make irrevocable decisions. We also explore whether state-of-the-art submodular optimization algorithms can be converted into descending auctions in adversarial settings, where the schedule of descending prices is determined by an adversary. We show that a submodular optimization algorithm satisfying bi-criteria $(1/2, 1)$-approximation in welfare can be effectively adapted to a descending auction. Additionally, we establish a connection between descending auctions and online submodular optimization. Finally, we demonstrate the practical applications of our frameworks by instantiating them with state-of-the-art submodular optimization algorithms and empirically comparing their welfare performance on publicly available datasets with thousands of sellers.

Computer-aided mechanism design: designing revenue-optimal mechanisms via neural networks

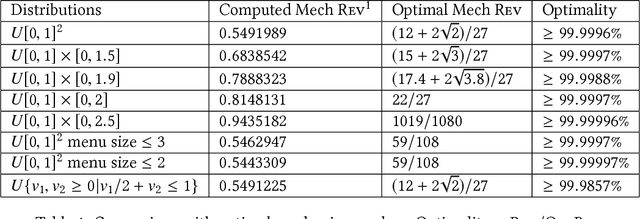
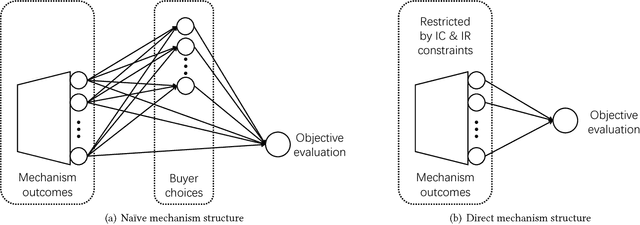
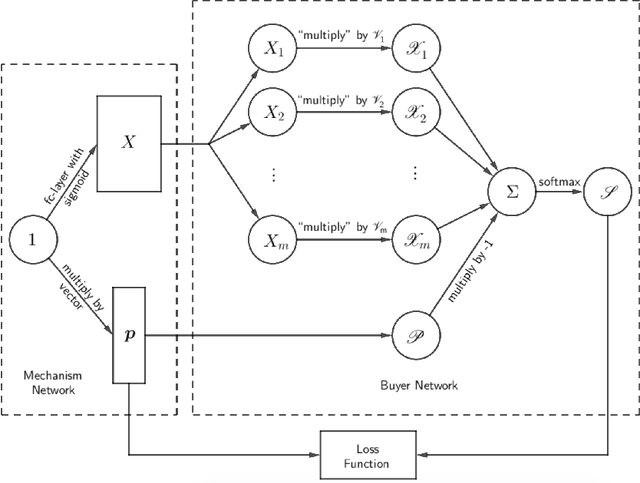
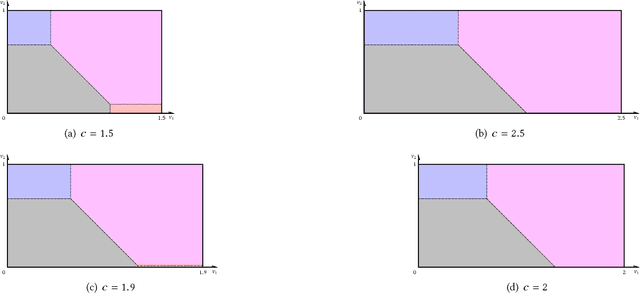
Using AI approaches to automatically design mechanisms has been a central research mission at the interface of AI and economics [Conitzer and Sandholm, 2002]. Previous approaches that a empt to design revenue optimal auctions for the multi-dimensional settings fall short in at least one of the three aspects: 1) representation --- search in a space that probably does not even contain the optimal mechanism; 2) exactness --- finding a mechanism that is either not truthful or far from optimal; 3) domain dependence --- need a different design for different environment settings. To resolve the three difficulties, in this paper, we put forward a uni ed neural network based framework that automatically learns to design revenue optimal mechanisms. Our framework consists of a mechanism network that takes an input distribution for training and outputs a mechanism, as well as a buyer network that takes a mechanism as input and output an action. Such a separation in design mitigates the difficulty to impose incentive compatibility constraints on the mechanism, by making it a rational choice of the buyer. As a result, our framework easily overcomes the previously mentioned difficulty in incorporating IC constraints and always returns exactly incentive compatible mechanisms. We then applied our framework to a number of multi-item revenue optimal design settings, for a few of which the theoretically optimal mechanisms are unknown. We then go on to theoretically prove that the mechanisms found by our framework are indeed optimal.

Optimal Vehicle Dispatching Schemes via Dynamic Pricing

Over the past few years, ride-sharing has emerged as an effective way to relieve traffic congestion. A key problem for these platforms is to come up with a revenue-optimal (or GMV-optimal) pricing scheme and an induced vehicle dispatching policy that incorporate geographic and temporal information. In this paper, we aim to tackle this problem via an economic approach. Modeled naively, the underlying optimization problem may be non-convex and thus hard to compute. To this end, we use a so-called "ironing" technique to convert the problem into an equivalent convex optimization one via a clean Markov decision process (MDP) formulation, where the states are the driver distributions and the decision variables are the prices for each pair of locations. Our main finding is an efficient algorithm that computes the exact revenue-optimal (or GMV-optimal) randomized pricing schemes. We characterize the optimal solution of the MDP by a primal-dual analysis of a corresponding convex program. We also conduct empirical evaluations of our solution through real data of a major ride-sharing platform and show its advantages over fixed pricing schemes as well as several prevalent surge-based pricing schemes.