Selling Joint Ads: A Regret Minimization Perspective
Paper and Code
Sep 12, 2024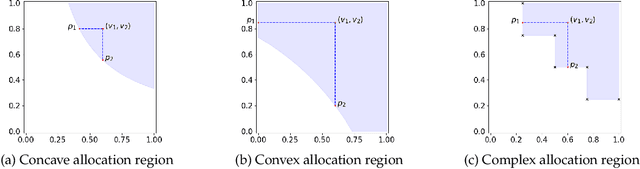
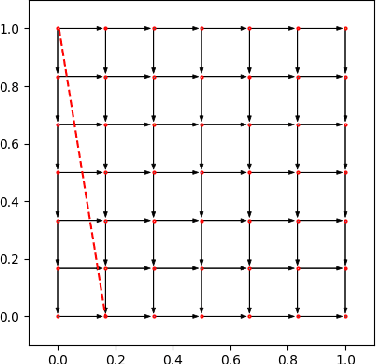
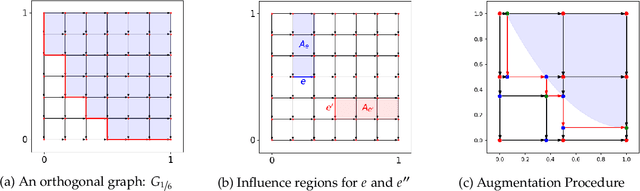
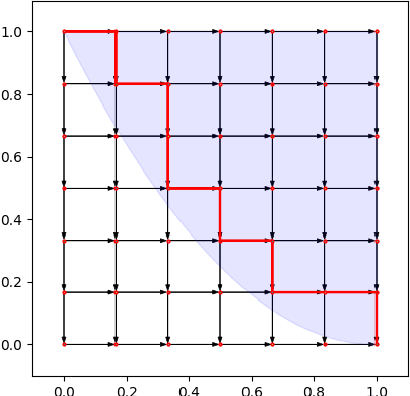
Motivated by online retail, we consider the problem of selling one item (e.g., an ad slot) to two non-excludable buyers (say, a merchant and a brand). This problem captures, for example, situations where a merchant and a brand cooperatively bid in an auction to advertise a product, and both benefit from the ad being shown. A mechanism collects bids from the two and decides whether to allocate and which payments the two parties should make. This gives rise to intricate incentive compatibility constraints, e.g., on how to split payments between the two parties. We approach the problem of finding a revenue-maximizing incentive-compatible mechanism from an online learning perspective; this poses significant technical challenges. First, the action space (the class of all possible mechanisms) is huge; second, the function that maps mechanisms to revenue is highly irregular, ruling out standard discretization-based approaches. In the stochastic setting, we design an efficient learning algorithm achieving a regret bound of $O(T^{3/4})$. Our approach is based on an adaptive discretization scheme of the space of mechanisms, as any non-adaptive discretization fails to achieve sublinear regret. In the adversarial setting, we exploit the non-Lipschitzness of the problem to prove a strong negative result, namely that no learning algorithm can achieve more than half of the revenue of the best fixed mechanism in hindsight. We then consider the $\sigma$-smooth adversary; we construct an efficient learning algorithm that achieves a regret bound of $O(T^{2/3})$ and builds on a succinct encoding of exponentially many experts. Finally, we prove that no learning algorithm can achieve less than $\Omega(\sqrt T)$ regret in both the stochastic and the smooth setting, thus narrowing the range where the minimax regret rates for these two problems lie.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge