Online Combinatorial Allocations and Auctions with Few Samples

In online combinatorial allocations/auctions, n bidders sequentially arrive, each with a combinatorial valuation (such as submodular/XOS) over subsets of m indivisible items. The aim is to immediately allocate a subset of the remaining items to maximize the total welfare, defined as the sum of bidder valuations. A long line of work has studied this problem when the bidder valuations come from known independent distributions. In particular, for submodular/XOS valuations, we know 2-competitive algorithms/mechanisms that set a fixed price for each item and the arriving bidders take their favorite subset of the remaining items given these prices. However, these algorithms traditionally presume the availability of the underlying distributions as part of the input to the algorithm. Contrary to this assumption, practical scenarios often require the learning of distributions, a task complicated by limited sample availability. This paper investigates the feasibility of achieving O(1)-competitive algorithms under the realistic constraint of having access to only a limited number of samples from the underlying bidder distributions. Our first main contribution shows that a mere single sample from each bidder distribution is sufficient to yield an O(1)-competitive algorithm for submodular/XOS valuations. This result leverages a novel extension of the secretary-style analysis, employing the sample to have the algorithm compete against itself. Although online, this first approach does not provide an online truthful mechanism. Our second main contribution shows that a polynomial number of samples suffices to yield a $(2+\epsilon)$-competitive online truthful mechanism for submodular/XOS valuations and any constant $\epsilon>0$. This result is based on a generalization of the median-based algorithm for the single-item prophet inequality problem to combinatorial settings with multiple items.

Online Algorithms with Limited Data Retention

We introduce a model of online algorithms subject to strict constraints on data retention. An online learning algorithm encounters a stream of data points, one per round, generated by some stationary process. Crucially, each data point can request that it be removed from memory $m$ rounds after it arrives. To model the impact of removal, we do not allow the algorithm to store any information or calculations between rounds other than a subset of the data points (subject to the retention constraints). At the conclusion of the stream, the algorithm answers a statistical query about the full dataset. We ask: what level of performance can be guaranteed as a function of $m$? We illustrate this framework for multidimensional mean estimation and linear regression problems. We show it is possible to obtain an exponential improvement over a baseline algorithm that retains all data as long as possible. Specifically, we show that $m = \textsc{Poly}(d, \log(1/\epsilon))$ retention suffices to achieve mean squared error $\epsilon$ after observing $O(1/\epsilon)$ $d$-dimensional data points. This matches the error bound of the optimal, yet infeasible, algorithm that retains all data forever. We also show a nearly matching lower bound on the retention required to guarantee error $\epsilon$. One implication of our results is that data retention laws are insufficient to guarantee the right to be forgotten even in a non-adversarial world in which firms merely strive to (approximately) optimize the performance of their algorithms. Our approach makes use of recent developments in the multidimensional random subset sum problem to simulate the progression of stochastic gradient descent under a model of adversarial noise, which may be of independent interest.

Impact of Decentralized Learning on Player Utilities in Stackelberg Games

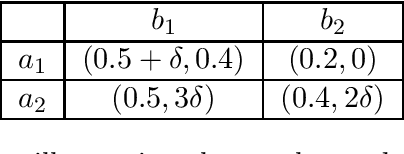
When deployed in the world, a learning agent such as a recommender system or a chatbot often repeatedly interacts with another learning agent (such as a user) over time. In many such two-agent systems, each agent learns separately and the rewards of the two agents are not perfectly aligned. To better understand such cases, we examine the learning dynamics of the two-agent system and the implications for each agent's objective. We model these systems as Stackelberg games with decentralized learning and show that standard regret benchmarks (such as Stackelberg equilibrium payoffs) result in worst-case linear regret for at least one player. To better capture these systems, we construct a relaxed regret benchmark that is tolerant to small learning errors by agents. We show that standard learning algorithms fail to provide sublinear regret, and we develop algorithms to achieve near-optimal $O(T^{2/3})$ regret for both players with respect to these benchmarks. We further design relaxed environments under which faster learning ($O(\sqrt{T})$) is possible. Altogether, our results take a step towards assessing how two-agent interactions in sequential and decentralized learning environments affect the utility of both agents.

Clickbait vs. Quality: How Engagement-Based Optimization Shapes the Content Landscape in Online Platforms

Online content platforms commonly use engagement-based optimization when making recommendations. This encourages content creators to invest in quality, but also rewards gaming tricks such as clickbait. To understand the total impact on the content landscape, we study a game between content creators competing on the basis of engagement metrics and analyze the equilibrium decisions about investment in quality and gaming. First, we show the content created at equilibrium exhibits a positive correlation between quality and gaming, and we empirically validate this finding on a Twitter dataset. Using the equilibrium structure of the content landscape, we then examine the downstream performance of engagement-based optimization along several axes. Perhaps counterintuitively, the average quality of content consumed by users can decrease at equilibrium as gaming tricks become more costly for content creators to employ. Moreover, engagement-based optimization can perform worse in terms of user utility than a baseline with random recommendations, and engagement-based optimization is also suboptimal in terms of realized engagement relative to quality-based optimization. Altogether, our results highlight the need to consider content creator incentives when evaluating a platform's choice of optimization metric.

Algorithmic Persuasion Through Simulation: Information Design in the Age of Generative AI

How can an informed sender persuade a receiver, having only limited information about the receiver's beliefs? Motivated by research showing generative AI can simulate economic agents, we initiate the study of information design with an oracle. We assume the sender can learn more about the receiver by querying this oracle, e.g., by simulating the receiver's behavior. Aside from AI motivations such as general-purpose Large Language Models (LLMs) and problem-specific machine learning models, alternate motivations include customer surveys and querying a small pool of live users. Specifically, we study Bayesian Persuasion where the sender has a second-order prior over the receiver's beliefs. After a fixed number of queries to an oracle to refine this prior, the sender commits to an information structure. Upon receiving the message, the receiver takes a payoff-relevant action maximizing her expected utility given her posterior beliefs. We design polynomial-time querying algorithms that optimize the sender's expected utility in this Bayesian Persuasion game. As a technical contribution, we show that queries form partitions of the space of receiver beliefs that can be used to quantify the sender's knowledge.

Autobidders with Budget and ROI Constraints: Efficiency, Regret, and Pacing Dynamics

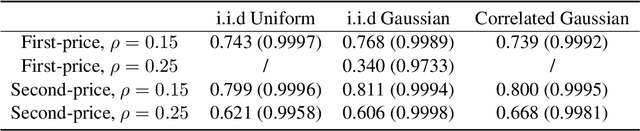
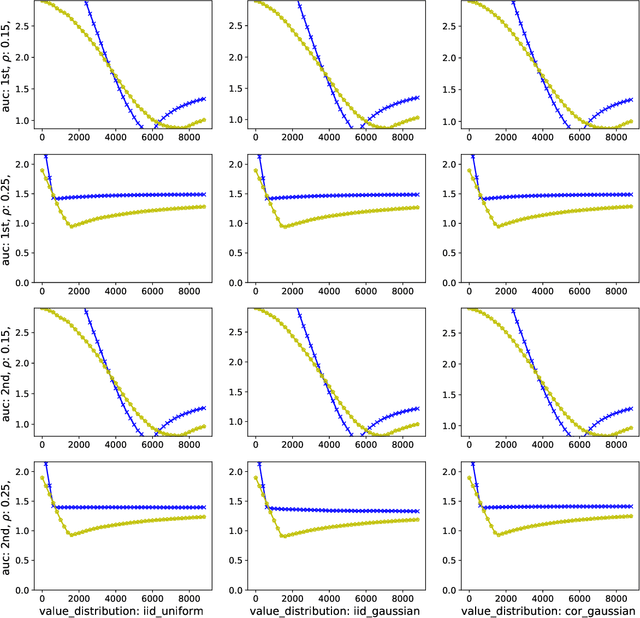
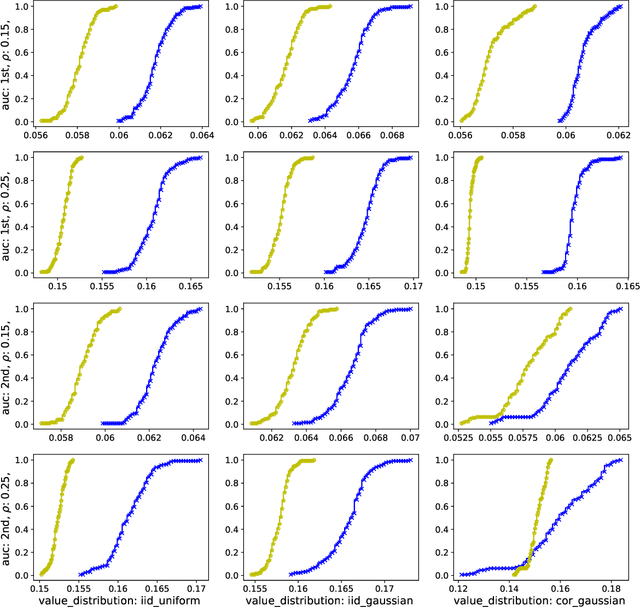
We study a game between autobidding algorithms that compete in an online advertising platform. Each autobidder is tasked with maximizing its advertiser's total value over multiple rounds of a repeated auction, subject to budget and/or return-on-investment constraints. We propose a gradient-based learning algorithm that is guaranteed to satisfy all constraints and achieves vanishing individual regret. Our algorithm uses only bandit feedback and can be used with the first- or second-price auction, as well as with any "intermediate" auction format. Our main result is that when these autobidders play against each other, the resulting expected liquid welfare over all rounds is at least half of the expected optimal liquid welfare achieved by any allocation. This holds whether or not the bidding dynamics converges to an equilibrium and regardless of the correlation structure between advertiser valuations.

Maximizing Welfare with Incentive-Aware Evaluation Mechanisms

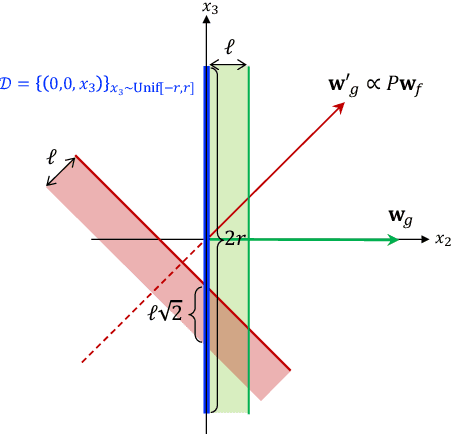
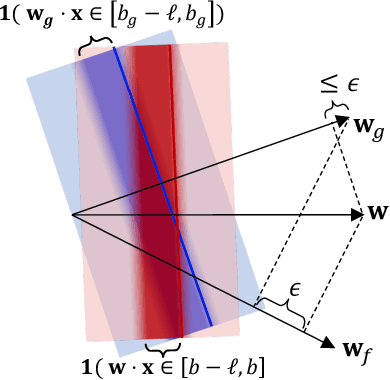
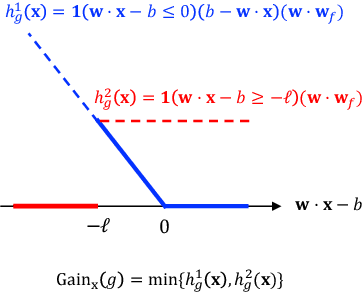
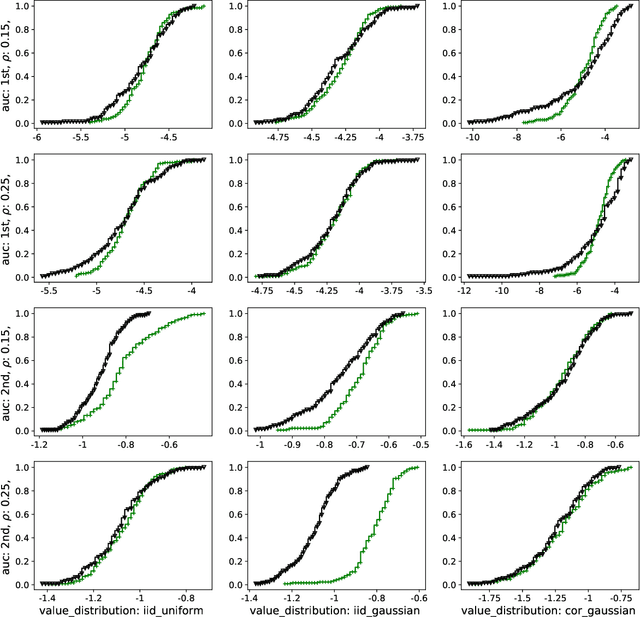
Motivated by applications such as college admission and insurance rate determination, we propose an evaluation problem where the inputs are controlled by strategic individuals who can modify their features at a cost. A learner can only partially observe the features, and aims to classify individuals with respect to a quality score. The goal is to design an evaluation mechanism that maximizes the overall quality score, i.e., welfare, in the population, taking any strategic updating into account. We further study the algorithmic aspect of finding the welfare maximizing evaluation mechanism under two specific settings in our model. When scores are linear and mechanisms use linear scoring rules on the observable features, we show that the optimal evaluation mechanism is an appropriate projection of the quality score. When mechanisms must use linear thresholds, we design a polynomial time algorithm with a (1/4)-approximation guarantee when the underlying feature distribution is sufficiently smooth and admits an oracle for finding dense regions. We extend our results to settings where the prior distribution is unknown and must be learned from samples.

Black-box Methods for Restoring Monotonicity

In many practical applications, heuristic or approximation algorithms are used to efficiently solve the task at hand. However their solutions frequently do not satisfy natural monotonicity properties of optimal solutions. In this work we develop algorithms that are able to restore monotonicity in the parameters of interest. Specifically, given oracle access to a (possibly non-monotone) multi-dimensional real-valued function $f$, we provide an algorithm that restores monotonicity while degrading the expected value of the function by at most $\varepsilon$. The number of queries required is at most logarithmic in $1/\varepsilon$ and exponential in the number of parameters. We also give a lower bound showing that this exponential dependence is necessary. Finally, we obtain improved query complexity bounds for restoring the weaker property of $k$-marginal monotonicity. Under this property, every $k$-dimensional projection of the function $f$ is required to be monotone. The query complexity we obtain only scales exponentially with $k$.

Procrastinating with Confidence: Near-Optimal, Anytime, Adaptive Algorithm Configuration

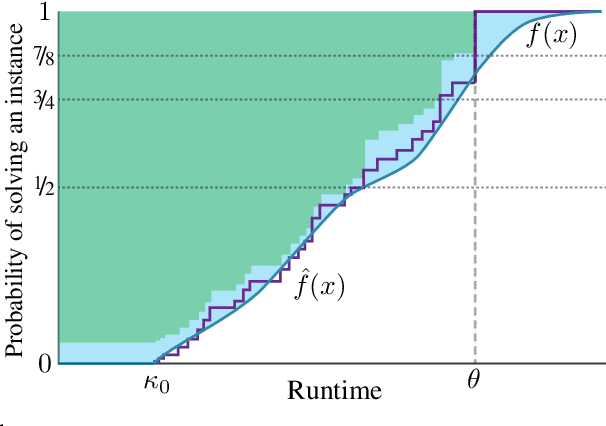
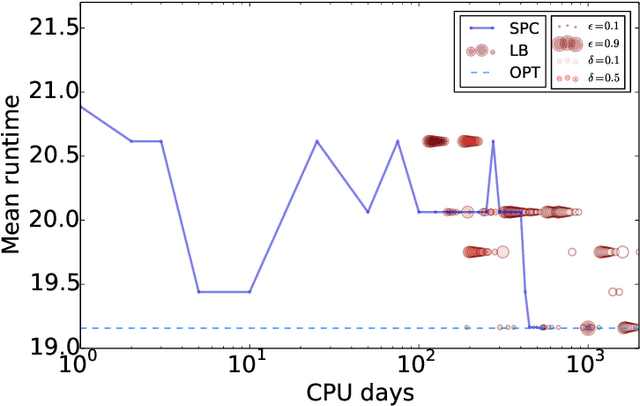
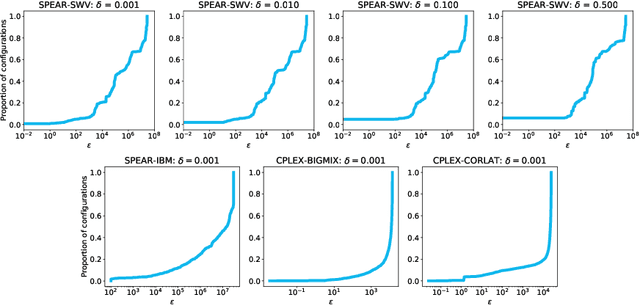
Algorithm configuration methods optimize the performance of a parameterized heuristic algorithm on a given distribution of problem instances. Recent work introduced an algorithm configuration procedure ('Structured Procrastination') that provably achieves near optimal performance with high probability and with nearly minimal runtime in the worst case. It also offers an $\textit{anytime}$ property: it keeps tightening its optimality guarantees the longer it is run. Unfortunately, Structured Procrastination is not $\textit{adaptive}$ to characteristics of the parameterized algorithm: it treats every input like the worst case. Follow-up work ('Leaps and Bounds') achieves adaptivity but trades away the anytime property. This paper introduces a new algorithm configuration method, 'Structured Procrastination with Confidence', that preserves the near-optimality and anytime properties of Structured Procrastination while adding adaptivity. In particular, the new algorithm will perform dramatically faster in settings where many algorithm configurations perform poorly; we show empirically that such settings arise frequently in practice.

Online Pandora's Boxes and Bandits

We consider online variations of the Pandora's box problem (Weitzman. 1979), a standard model for understanding issues related to the cost of acquiring information for decision-making. Our problem generalizes both the classic Pandora's box problem and the prophet inequality framework. Boxes are presented online, each with a random value and cost drew jointly from some known distribution. Pandora chooses online whether to open each box given its cost, and then chooses irrevocably whether to keep the revealed prize or pass on it. We aim for approximation algorithms against adversaries that can choose the largest prize over any opened box, and use optimal offline policies to decide which boxes to open (without knowledge of the value inside). We consider variations where Pandora can collect multiple prizes subject to feasibility constraints, such as cardinality, matroid, or knapsack constraints. We also consider variations related to classic multi-armed bandit problems from reinforcement learning. Our results use a reduction-based framework where we separate the issues of the cost of acquiring information from the online decision process of which prizes to keep. Our work shows that in many scenarios, Pandora can achieve a good approximation to the best possible performance.