Autobidders with Budget and ROI Constraints: Efficiency, Regret, and Pacing Dynamics

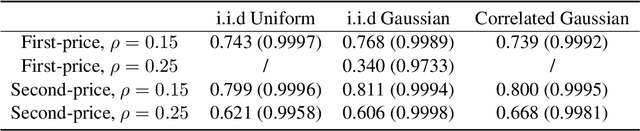
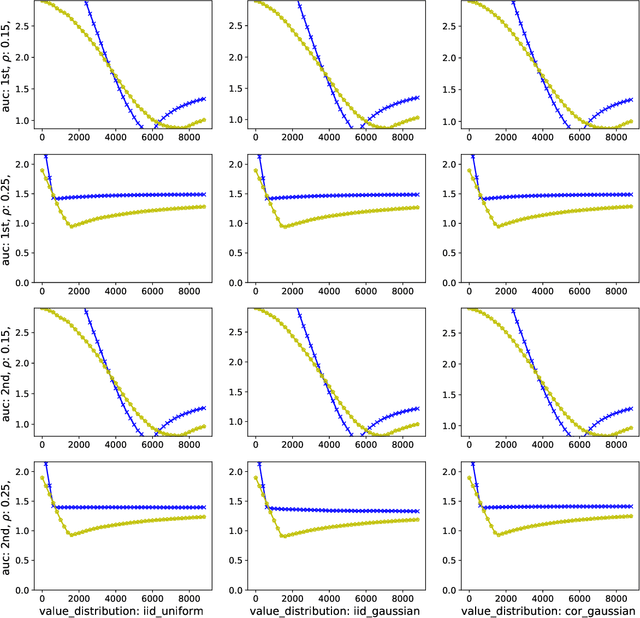
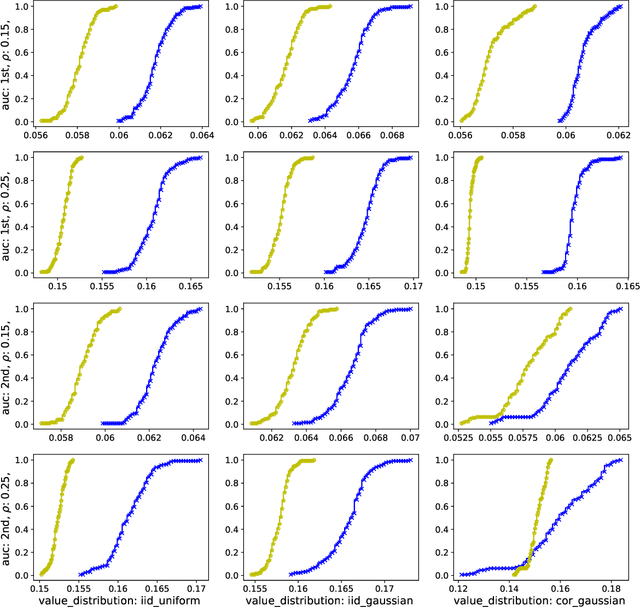
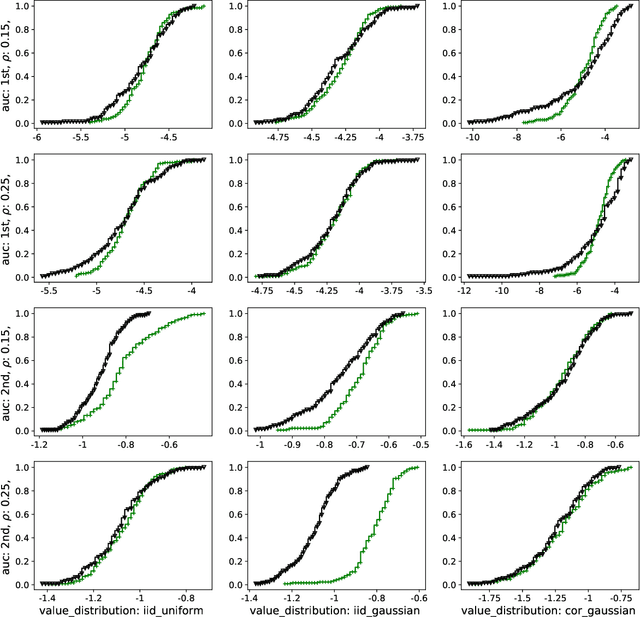
We study a game between autobidding algorithms that compete in an online advertising platform. Each autobidder is tasked with maximizing its advertiser's total value over multiple rounds of a repeated auction, subject to budget and/or return-on-investment constraints. We propose a gradient-based learning algorithm that is guaranteed to satisfy all constraints and achieves vanishing individual regret. Our algorithm uses only bandit feedback and can be used with the first- or second-price auction, as well as with any "intermediate" auction format. Our main result is that when these autobidders play against each other, the resulting expected liquid welfare over all rounds is at least half of the expected optimal liquid welfare achieved by any allocation. This holds whether or not the bidding dynamics converges to an equilibrium and regardless of the correlation structure between advertiser valuations.

Revisiting the Linear-Programming Framework for Offline RL with General Function Approximation

Offline reinforcement learning (RL) concerns pursuing an optimal policy for sequential decision-making from a pre-collected dataset, without further interaction with the environment. Recent theoretical progress has focused on developing sample-efficient offline RL algorithms with various relaxed assumptions on data coverage and function approximators, especially to handle the case with excessively large state-action spaces. Among them, the framework based on the linear-programming (LP) reformulation of Markov decision processes has shown promise: it enables sample-efficient offline RL with function approximation, under only partial data coverage and realizability assumptions on the function classes, with favorable computational tractability. In this work, we revisit the LP framework for offline RL, and advance the existing results in several aspects, relaxing certain assumptions and achieving optimal statistical rates in terms of sample size. Our key enabler is to introduce proper constraints in the reformulation, instead of using any regularization as in the literature, sometimes also with careful choices of the function classes and initial state distributions. We hope our insights further advocate the study of the LP framework, as well as the induced primal-dual minimax optimization, in offline RL.

Symmetric (Optimistic) Natural Policy Gradient for Multi-agent Learning with Parameter Convergence

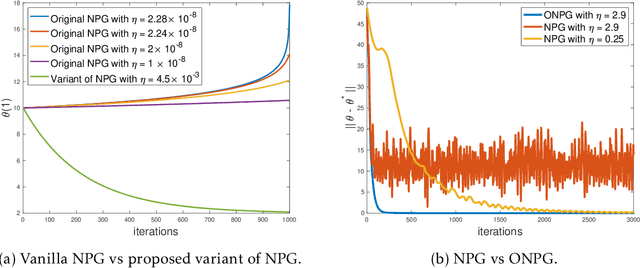
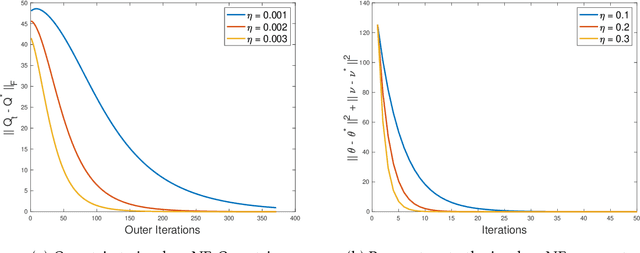
Multi-agent interactions are increasingly important in the context of reinforcement learning, and the theoretical foundations of policy gradient methods have attracted surging research interest. We investigate the global convergence of natural policy gradient (NPG) algorithms in multi-agent learning. We first show that vanilla NPG may not have parameter convergence, i.e., the convergence of the vector that parameterizes the policy, even when the costs are regularized (which enabled strong convergence guarantees in the policy space in the literature). This non-convergence of parameters leads to stability issues in learning, which becomes especially relevant in the function approximation setting, where we can only operate on low-dimensional parameters, instead of the high-dimensional policy. We then propose variants of the NPG algorithm, for several standard multi-agent learning scenarios: two-player zero-sum matrix and Markov games, and multi-player monotone games, with global last-iterate parameter convergence guarantees. We also generalize the results to certain function approximation settings. Note that in our algorithms, the agents take symmetric roles. Our results might also be of independent interest for solving nonconvex-nonconcave minimax optimization problems with certain structures. Simulations are also provided to corroborate our theoretical findings.

What is a Good Metric to Study Generalization of Minimax Learners?

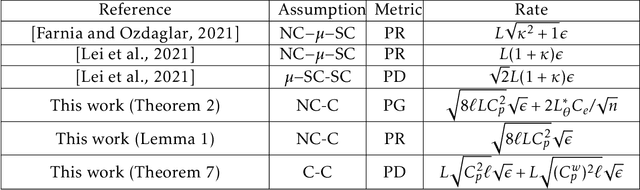
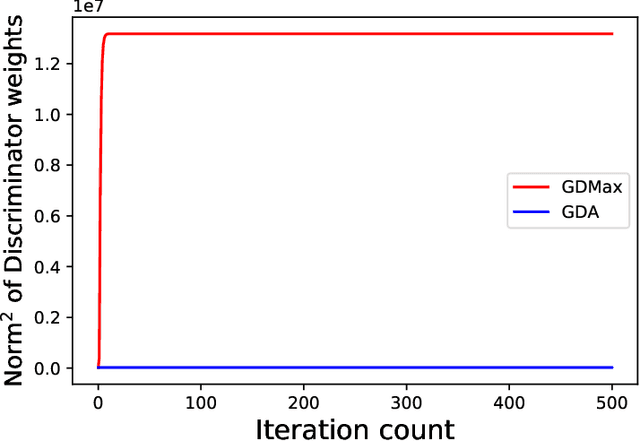
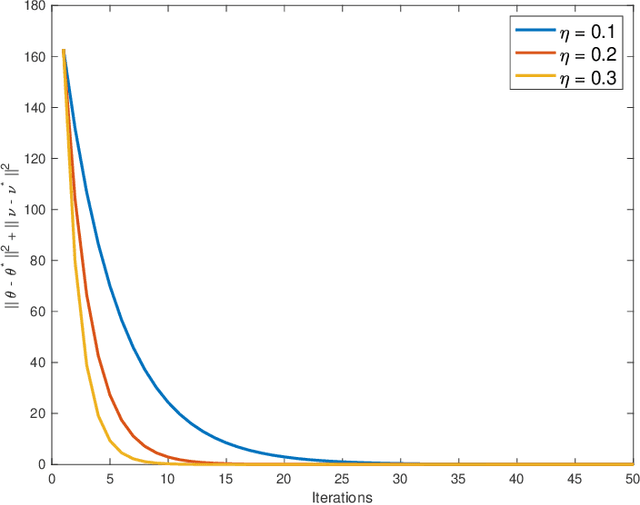
Minimax optimization has served as the backbone of many machine learning (ML) problems. Although the convergence behavior of optimization algorithms has been extensively studied in the minimax settings, their generalization guarantees in stochastic minimax optimization problems, i.e., how the solution trained on empirical data performs on unseen testing data, have been relatively underexplored. A fundamental question remains elusive: What is a good metric to study generalization of minimax learners? In this paper, we aim to answer this question by first showing that primal risk, a universal metric to study generalization in minimization problems, which has also been adopted recently to study generalization in minimax ones, fails in simple examples. We thus propose a new metric to study generalization of minimax learners: the primal gap, defined as the difference between the primal risk and its minimum over all models, to circumvent the issues. Next, we derive generalization error bounds for the primal gap in nonconvex-concave settings. As byproducts of our analysis, we also solve two open questions: establishing generalization error bounds for primal risk and primal-dual risk, another existing metric that is only well-defined when the global saddle-point exists, in the strong sense, i.e., without strong concavity or assuming that the maximization and expectation can be interchanged, while either of these assumptions was needed in the literature. Finally, we leverage this new metric to compare the generalization behavior of two popular algorithms -- gradient descent-ascent (GDA) and gradient descent-max (GDMax) in stochastic minimax optimization.

Tight last-iterate convergence rates for no-regret learning in multi-player games

We study the question of obtaining last-iterate convergence rates for no-regret learning algorithms in multi-player games. We show that the optimistic gradient (OG) algorithm with a constant step-size, which is no-regret, achieves a last-iterate rate of $O(1/\sqrt{T})$ with respect to the gap function in smooth monotone games. This result addresses a question of Mertikopoulos & Zhou (2018), who asked whether extra-gradient approaches (such as OG) can be applied to achieve improved guarantees in the multi-agent learning setting. The proof of our upper bound uses a new technique centered around an adaptive choice of potential function at each iteration. We also show that the $O(1/\sqrt{T})$ rate is tight for all $p$-SCLI algorithms, which includes OG as a special case. As a byproduct of our lower bound analysis we additionally present a proof of a conjecture of Arjevani et al. (2015) which is more direct than previous approaches.

An Optimal Multistage Stochastic Gradient Method for Minimax Problems

In this paper, we study the minimax optimization problem in the smooth and strongly convex-strongly concave setting when we have access to noisy estimates of gradients. In particular, we first analyze the stochastic Gradient Descent Ascent (GDA) method with constant stepsize, and show that it converges to a neighborhood of the solution of the minimax problem. We further provide tight bounds on the convergence rate and the size of this neighborhood. Next, we propose a multistage variant of stochastic GDA (M-GDA) that runs in multiple stages with a particular learning rate decay schedule and converges to the exact solution of the minimax problem. We show M-GDA achieves the lower bounds in terms of noise dependence without any assumptions on the knowledge of noise characteristics. We also show that M-GDA obtains a linear decay rate with respect to the error's dependence on the initial error, although the dependence on condition number is suboptimal. In order to improve this dependence, we apply the multistage machinery to the stochastic Optimistic Gradient Descent Ascent (OGDA) algorithm and propose the M-OGDA algorithm which also achieves the optimal linear decay rate with respect to the initial error. To the best of our knowledge, this method is the first to simultaneously achieve the best dependence on noise characteristic as well as the initial error and condition number.

Last Iterate is Slower than Averaged Iterate in Smooth Convex-Concave Saddle Point Problems

In this paper we study the smooth convex-concave saddle point problem. Specifically, we analyze the last iterate convergence properties of the Extragradient (EG) algorithm. It is well known that the ergodic (averaged) iterates of EG converge at a rate of $O(1/T)$ (Nemirovski, 2004). In this paper, we show that the last iterate of EG converges at a rate of $O(1/\sqrt{T})$. To the best of our knowledge, this is the first paper to provide a convergence rate guarantee for the last iterate of EG for the smooth convex-concave saddle point problem. Moreover, we show that this rate is tight by proving a lower bound of $\Omega(1/\sqrt{T})$ for the last iterate. This lower bound therefore shows a quadratic separation of the convergence rates of ergodic and last iterates in smooth convex-concave saddle point problems.

A Decentralized Proximal Point-type Method for Saddle Point Problems

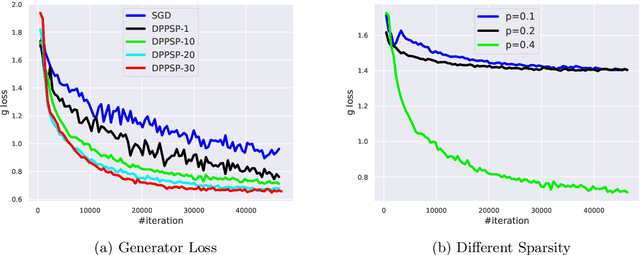
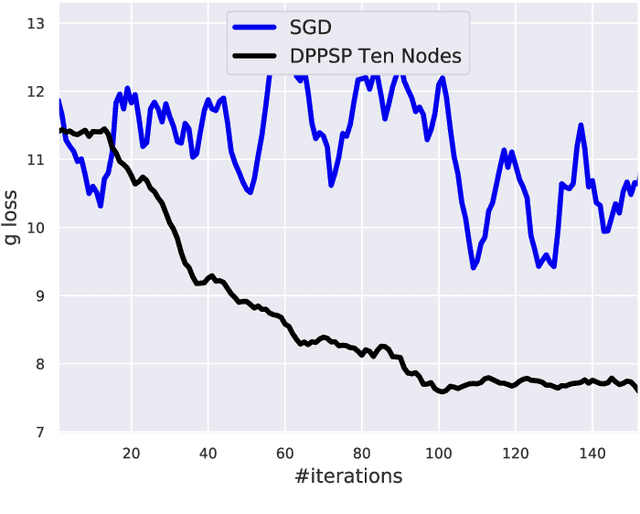
In this paper, we focus on solving a class of constrained non-convex non-concave saddle point problems in a decentralized manner by a group of nodes in a network. Specifically, we assume that each node has access to a summand of a global objective function and nodes are allowed to exchange information only with their neighboring nodes. We propose a decentralized variant of the proximal point method for solving this problem. We show that when the objective function is $\rho$-weakly convex-weakly concave the iterates converge to approximate stationarity with a rate of $\mathcal{O}(1/\sqrt{T})$ where the approximation error depends linearly on $\sqrt{\rho}$. We further show that when the objective function satisfies the Minty VI condition (which generalizes the convex-concave case) we obtain convergence to stationarity with a rate of $\mathcal{O}(1/\sqrt{T})$. To the best of our knowledge, our proposed method is the first decentralized algorithm with theoretical guarantees for solving a non-convex non-concave decentralized saddle point problem. Our numerical results for training a general adversarial network (GAN) in a decentralized manner match our theoretical guarantees.

Proximal Point Approximations Achieving a Convergence Rate of $\mathcal{O}(1/k)$ for Smooth Convex-Concave Saddle Point Problems: Optimistic Gradient and Extra-gradient Methods

In this paper we analyze the iteration complexity of the optimistic gradient descent-ascent (OGDA) method as well as the extra-gradient (EG) method for finding a saddle point of a convex-concave unconstrained min-max problem. To do so, we first show that both OGDA and EG can be interpreted as approximate variants of the proximal point method. We then exploit this interpretation to show that both of these algorithms achieve a convergence rate of $\mathcal{O}(1/k)$ for smooth convex-concave saddle point problems. Our theoretical analysis is of interest as it provides a simple convergence analysis for the EG algorithm in terms of objective function value without using compactness assumption. Moreover, it provides the first convergence guarantee for OGDA in the general convex-concave setting.

A Unified Analysis of Extra-gradient and Optimistic Gradient Methods for Saddle Point Problems: Proximal Point Approach

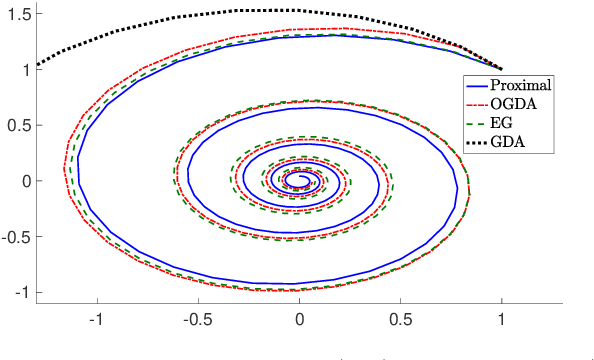
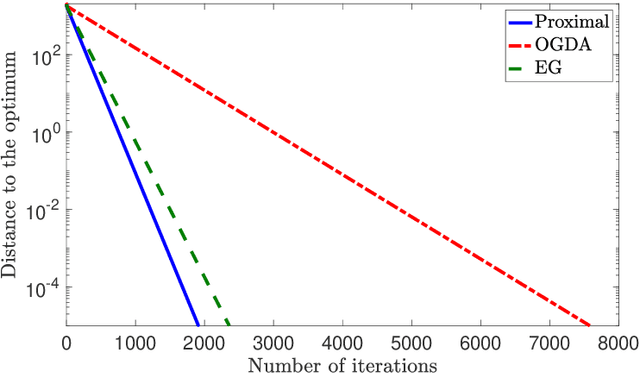
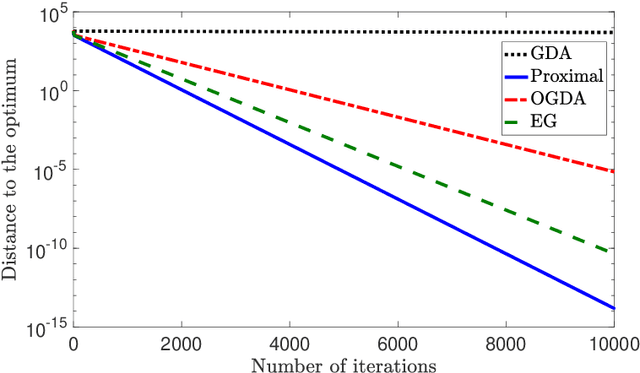
We consider solving convex-concave saddle point problems. We focus on two variants of gradient decent-ascent algorithms, Extra-gradient (EG) and Optimistic Gradient (OGDA) methods, and show that they admit a unified analysis as approximations of the classical proximal point method for solving saddle-point problems. This viewpoint enables us to generalize EG (in terms of extrapolation steps) and OGDA (in terms of parameters) and obtain new convergence rate results for these algorithms for the bilinear case as well as the strongly convex-concave case.