A Decentralized Proximal Point-type Method for Saddle Point Problems
Paper and Code
Oct 31, 2019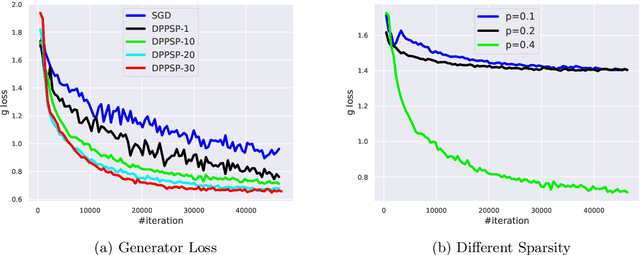

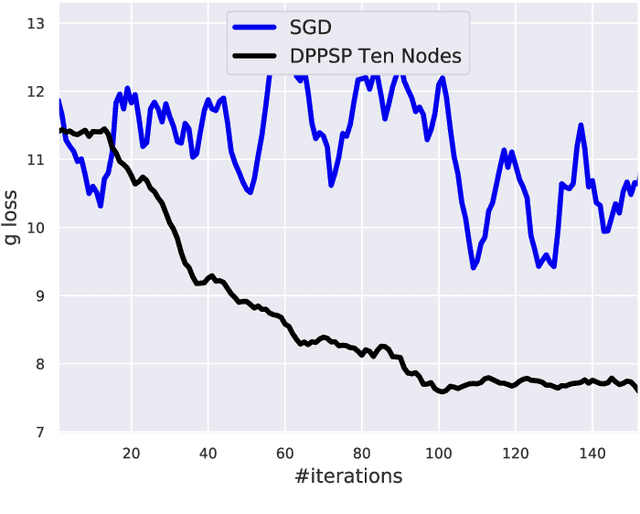
In this paper, we focus on solving a class of constrained non-convex non-concave saddle point problems in a decentralized manner by a group of nodes in a network. Specifically, we assume that each node has access to a summand of a global objective function and nodes are allowed to exchange information only with their neighboring nodes. We propose a decentralized variant of the proximal point method for solving this problem. We show that when the objective function is $\rho$-weakly convex-weakly concave the iterates converge to approximate stationarity with a rate of $\mathcal{O}(1/\sqrt{T})$ where the approximation error depends linearly on $\sqrt{\rho}$. We further show that when the objective function satisfies the Minty VI condition (which generalizes the convex-concave case) we obtain convergence to stationarity with a rate of $\mathcal{O}(1/\sqrt{T})$. To the best of our knowledge, our proposed method is the first decentralized algorithm with theoretical guarantees for solving a non-convex non-concave decentralized saddle point problem. Our numerical results for training a general adversarial network (GAN) in a decentralized manner match our theoretical guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge