The Statistical Fairness-Accuracy Frontier

Machine learning models must balance accuracy and fairness, but these goals often conflict, particularly when data come from multiple demographic groups. A useful tool for understanding this trade-off is the fairness-accuracy (FA) frontier, which characterizes the set of models that cannot be simultaneously improved in both fairness and accuracy. Prior analyses of the FA frontier provide a full characterization under the assumption of complete knowledge of population distributions -- an unrealistic ideal. We study the FA frontier in the finite-sample regime, showing how it deviates from its population counterpart and quantifying the worst-case gap between them. In particular, we derive minimax-optimal estimators that depend on the designer's knowledge of the covariate distribution. For each estimator, we characterize how finite-sample effects asymmetrically impact each group's risk, and identify optimal sample allocation strategies. Our results transform the FA frontier from a theoretical construct into a practical tool for policymakers and practitioners who must often design algorithms with limited data.

A General Framework for Estimating Preferences Using Response Time Data

We propose a general methodology for recovering preference parameters from data on choices and response times. Our methods yield estimates with fast ($1/n$ for $n$ data points) convergence rates when specialized to the popular Drift Diffusion Model (DDM), but are broadly applicable to generalizations of the DDM as well as to alternative models of decision making that make use of response time data. The paper develops an empirical application to an experiment on intertemporal choice, showing that the use of response times delivers predictive accuracy and matters for the estimation of economically relevant parameters.

Enhancing Feature-Specific Data Protection via Bayesian Coordinate Differential Privacy

Local Differential Privacy (LDP) offers strong privacy guarantees without requiring users to trust external parties. However, LDP applies uniform protection to all data features, including less sensitive ones, which degrades performance of downstream tasks. To overcome this limitation, we propose a Bayesian framework, Bayesian Coordinate Differential Privacy (BCDP), that enables feature-specific privacy quantification. This more nuanced approach complements LDP by adjusting privacy protection according to the sensitivity of each feature, enabling improved performance of downstream tasks without compromising privacy. We characterize the properties of BCDP and articulate its connections with standard non-Bayesian privacy frameworks. We further apply our BCDP framework to the problems of private mean estimation and ordinary least-squares regression. The BCDP-based approach obtains improved accuracy compared to a purely LDP-based approach, without compromising on privacy.

Fair Allocation in Dynamic Mechanism Design

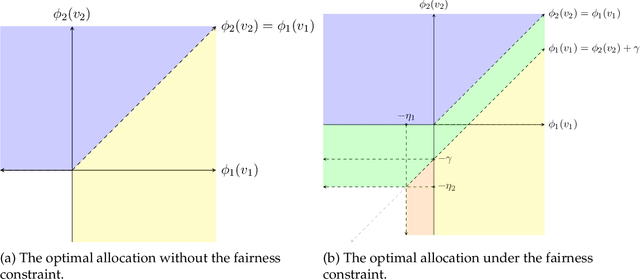
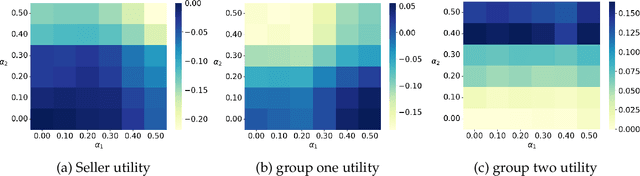
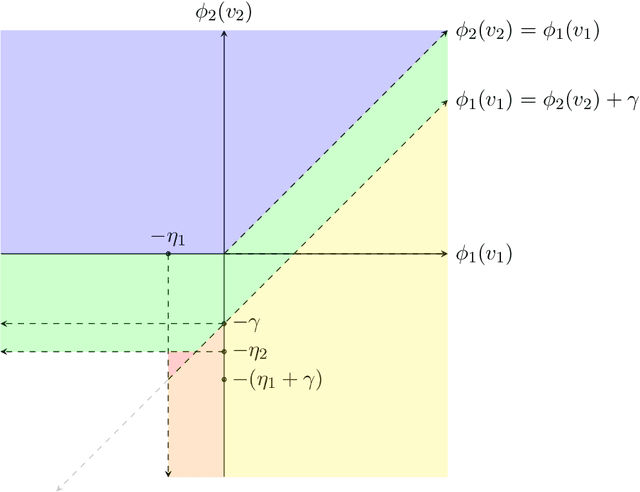
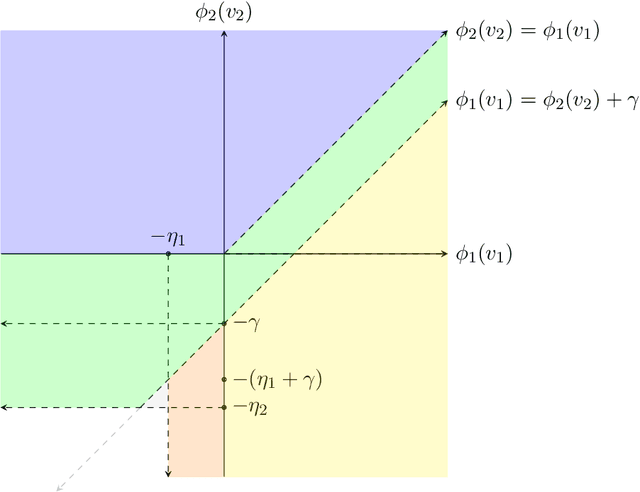
We consider a dynamic mechanism design problem where an auctioneer sells an indivisible good to two groups of buyers in every round, for a total of $T$ rounds. The auctioneer aims to maximize their discounted overall revenue while adhering to a fairness constraint that guarantees a minimum average allocation for each group. We begin by studying the static case ($T=1$) and establish that the optimal mechanism involves two types of subsidization: one that increases the overall probability of allocation to all buyers, and another that favors the group which otherwise has a lower probability of winning the item. We then extend our results to the dynamic case by characterizing a set of recursive functions that determine the optimal allocation and payments in each round. Notably, our results establish that in the dynamic case, the seller, on the one hand, commits to a participation reward to incentivize truth-telling, and on the other hand, charges an entry fee for every round. Moreover, the optimal allocation once more involves subsidization in favor of one group, where the extent of subsidization depends on the difference in future utilities for both the seller and buyers when allocating the item to one group versus the other. Finally, we present an approximation scheme to solve the recursive equations and determine an approximately optimal and fair allocation efficiently.

Optimal and Differentially Private Data Acquisition: Central and Local Mechanisms

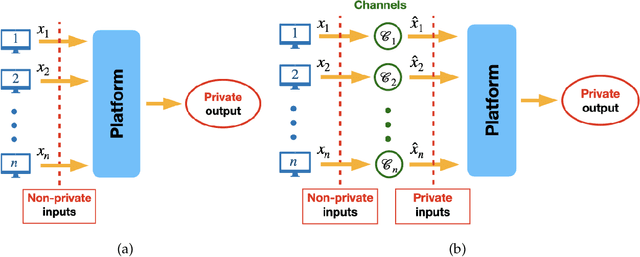
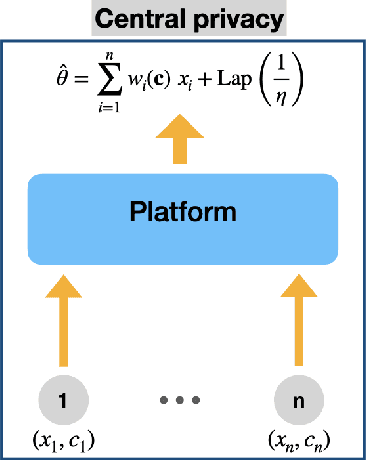
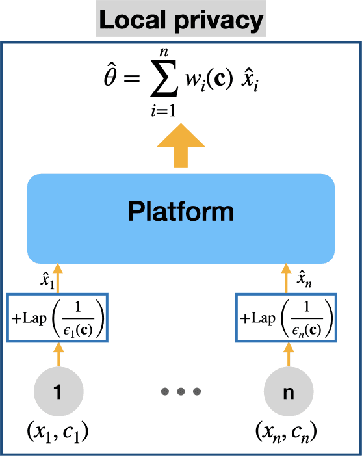
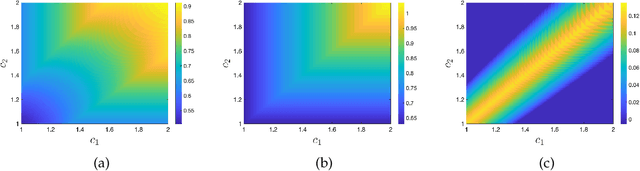
We consider a platform's problem of collecting data from privacy sensitive users to estimate an underlying parameter of interest. We formulate this question as a Bayesian-optimal mechanism design problem, in which an individual can share her (verifiable) data in exchange for a monetary reward or services, but at the same time has a (private) heterogeneous privacy cost which we quantify using differential privacy. We consider two popular differential privacy settings for providing privacy guarantees for the users: central and local. In both settings, we establish minimax lower bounds for the estimation error and derive (near) optimal estimators for given heterogeneous privacy loss levels for users. Building on this characterization, we pose the mechanism design problem as the optimal selection of an estimator and payments that will elicit truthful reporting of users' privacy sensitivities. Under a regularity condition on the distribution of privacy sensitivities we develop efficient algorithmic mechanisms to solve this problem in both privacy settings. Our mechanism in the central setting can be implemented in time $\mathcal{O}(n \log n)$ where $n$ is the number of users and our mechanism in the local setting admits a Polynomial Time Approximation Scheme (PTAS).

Private Adaptive Gradient Methods for Convex Optimization

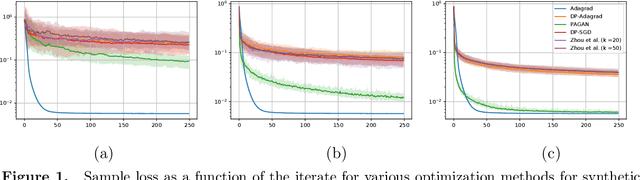
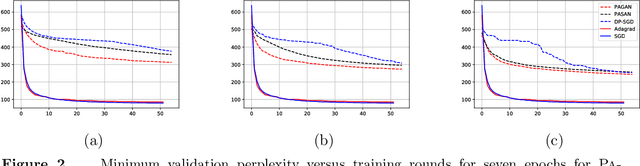
We study adaptive methods for differentially private convex optimization, proposing and analyzing differentially private variants of a Stochastic Gradient Descent (SGD) algorithm with adaptive stepsizes, as well as the AdaGrad algorithm. We provide upper bounds on the regret of both algorithms and show that the bounds are (worst-case) optimal. As a consequence of our development, we show that our private versions of AdaGrad outperform adaptive SGD, which in turn outperforms traditional SGD in scenarios with non-isotropic gradients where (non-private) Adagrad provably outperforms SGD. The major challenge is that the isotropic noise typically added for privacy dominates the signal in gradient geometry for high-dimensional problems; approaches to this that effectively optimize over lower-dimensional subspaces simply ignore the actual problems that varying gradient geometries introduce. In contrast, we study non-isotropic clipping and noise addition, developing a principled theoretical approach; the consequent procedures also enjoy significantly stronger empirical performance than prior approaches.

A Wasserstein Minimax Framework for Mixed Linear Regression

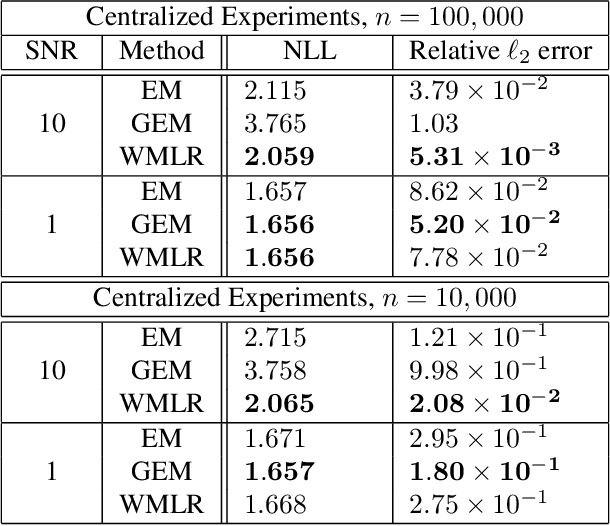
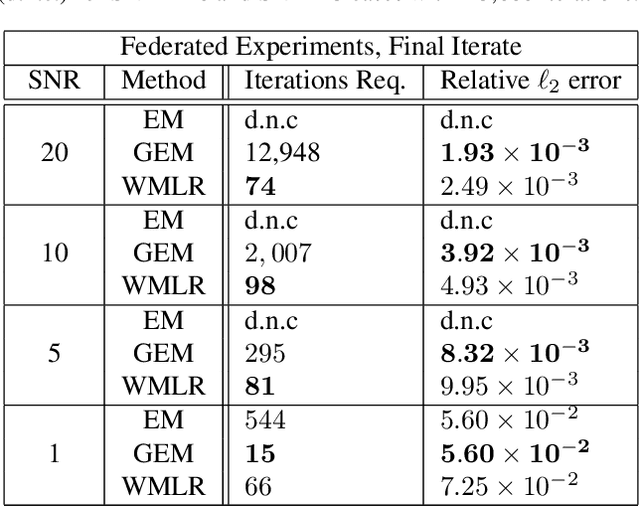
Multi-modal distributions are commonly used to model clustered data in statistical learning tasks. In this paper, we consider the Mixed Linear Regression (MLR) problem. We propose an optimal transport-based framework for MLR problems, Wasserstein Mixed Linear Regression (WMLR), which minimizes the Wasserstein distance between the learned and target mixture regression models. Through a model-based duality analysis, WMLR reduces the underlying MLR task to a nonconvex-concave minimax optimization problem, which can be provably solved to find a minimax stationary point by the Gradient Descent Ascent (GDA) algorithm. In the special case of mixtures of two linear regression models, we show that WMLR enjoys global convergence and generalization guarantees. We prove that WMLR's sample complexity grows linearly with the dimension of data. Finally, we discuss the application of WMLR to the federated learning task where the training samples are collected by multiple agents in a network. Unlike the Expectation Maximization algorithm, WMLR directly extends to the distributed, federated learning setting. We support our theoretical results through several numerical experiments, which highlight our framework's ability to handle the federated learning setting with mixture models.

Generalization of Model-Agnostic Meta-Learning Algorithms: Recurring and Unseen Tasks

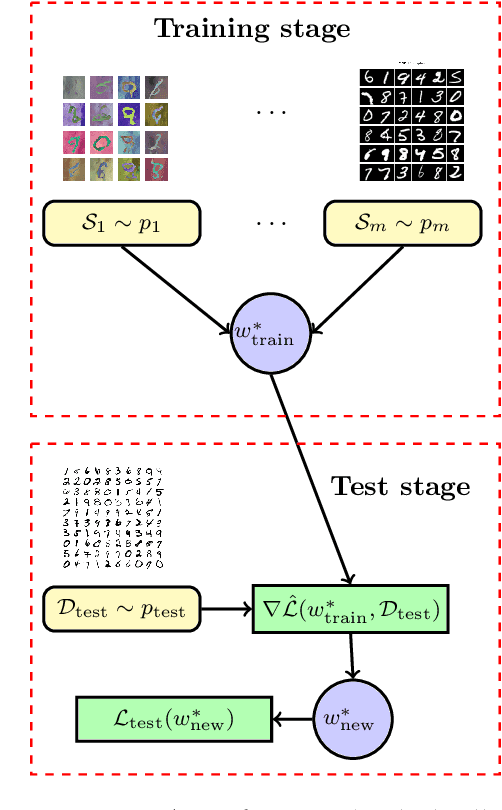
In this paper, we study the generalization properties of Model-Agnostic Meta-Learning (MAML) algorithms for supervised learning problems. We focus on the setting in which we train the MAML model over $m$ tasks, each with $n$ data points, and characterize its generalization error from two points of view: First, we assume the new task at test time is one of the training tasks, and we show that, for strongly convex objective functions, the expected excess population loss is bounded by $\mathcal{O}(1/mn)$. Second, we consider the MAML algorithm's generalization to an unseen task and show that the resulting generalization error depends on the total variation distance between the underlying distributions of the new task and the tasks observed during the training process. Our proof techniques rely on the connections between algorithmic stability and generalization bounds of algorithms. In particular, we propose a new definition of stability for meta-learning algorithms, which allows us to capture the role of both the number of tasks $m$ and number of samples per task $n$ on the generalization error of MAML.

Personalized Federated Learning: A Meta-Learning Approach

The goal of federated learning is to design algorithms in which several agents communicate with a central node, in a privacy-protecting manner, to minimize the average of their loss functions. In this approach, each node not only shares the required computational budget but also has access to a larger data set, which improves the quality of the resulting model. However, this method only develops a common output for all the agents, and therefore, does not adapt the model to each user data. This is an important missing feature especially given the heterogeneity of the underlying data distribution for various agents. In this paper, we study a personalized variant of the federated learning in which our goal is to find a shared initial model in a distributed manner that can be slightly updated by either a current or a new user by performing one or a few steps of gradient descent with respect to its own loss function. This approach keeps all the benefits of the federated learning architecture while leading to a more personalized model for each user. We show this problem can be studied within the Model-Agnostic Meta-Learning (MAML) framework. Inspired by this connection, we propose a personalized variant of the well-known Federated Averaging algorithm and evaluate its performance in terms of gradient norm for non-convex loss functions. Further, we characterize how this performance is affected by the closeness of underlying distributions of user data, measured in terms of distribution distances such as Total Variation and 1-Wasserstein metric.

An Optimal Multistage Stochastic Gradient Method for Minimax Problems

In this paper, we study the minimax optimization problem in the smooth and strongly convex-strongly concave setting when we have access to noisy estimates of gradients. In particular, we first analyze the stochastic Gradient Descent Ascent (GDA) method with constant stepsize, and show that it converges to a neighborhood of the solution of the minimax problem. We further provide tight bounds on the convergence rate and the size of this neighborhood. Next, we propose a multistage variant of stochastic GDA (M-GDA) that runs in multiple stages with a particular learning rate decay schedule and converges to the exact solution of the minimax problem. We show M-GDA achieves the lower bounds in terms of noise dependence without any assumptions on the knowledge of noise characteristics. We also show that M-GDA obtains a linear decay rate with respect to the error's dependence on the initial error, although the dependence on condition number is suboptimal. In order to improve this dependence, we apply the multistage machinery to the stochastic Optimistic Gradient Descent Ascent (OGDA) algorithm and propose the M-OGDA algorithm which also achieves the optimal linear decay rate with respect to the initial error. To the best of our knowledge, this method is the first to simultaneously achieve the best dependence on noise characteristic as well as the initial error and condition number.