Ali Makhdoumi
Optimal and Differentially Private Data Acquisition: Central and Local Mechanisms
Jan 10, 2022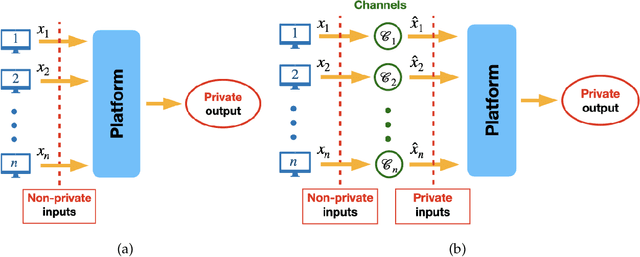
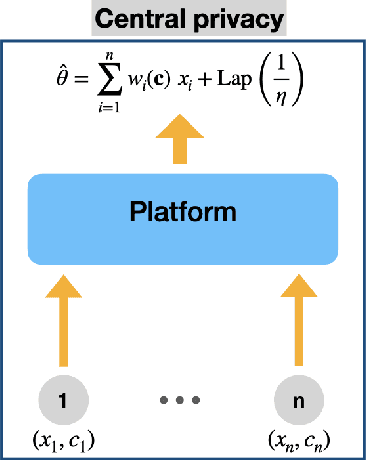
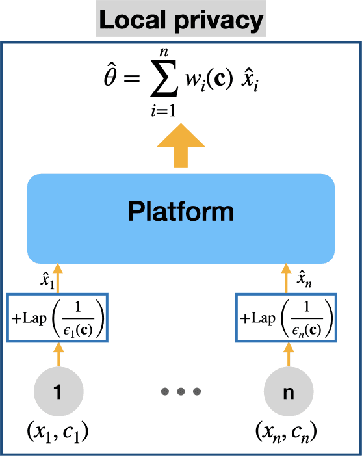
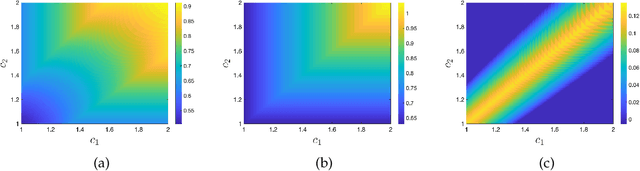
Abstract:We consider a platform's problem of collecting data from privacy sensitive users to estimate an underlying parameter of interest. We formulate this question as a Bayesian-optimal mechanism design problem, in which an individual can share her (verifiable) data in exchange for a monetary reward or services, but at the same time has a (private) heterogeneous privacy cost which we quantify using differential privacy. We consider two popular differential privacy settings for providing privacy guarantees for the users: central and local. In both settings, we establish minimax lower bounds for the estimation error and derive (near) optimal estimators for given heterogeneous privacy loss levels for users. Building on this characterization, we pose the mechanism design problem as the optimal selection of an estimator and payments that will elicit truthful reporting of users' privacy sensitivities. Under a regularity condition on the distribution of privacy sensitivities we develop efficient algorithmic mechanisms to solve this problem in both privacy settings. Our mechanism in the central setting can be implemented in time $\mathcal{O}(n \log n)$ where $n$ is the number of users and our mechanism in the local setting admits a Polynomial Time Approximation Scheme (PTAS).
Network Maximal Correlation
Feb 09, 2017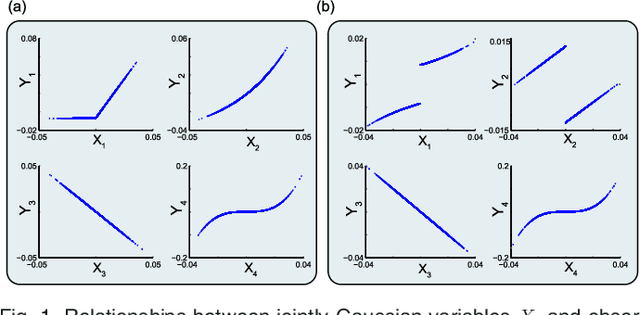
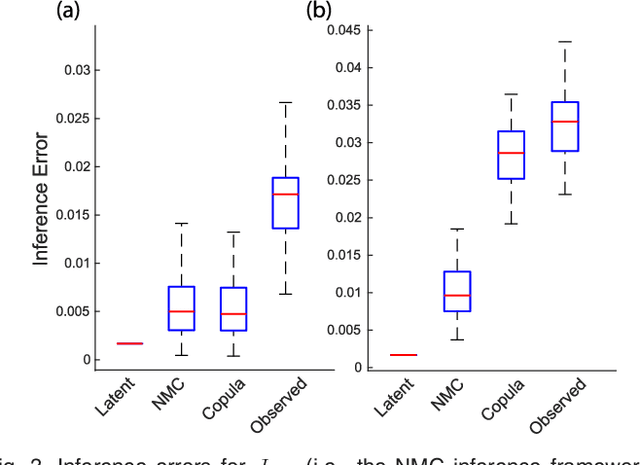
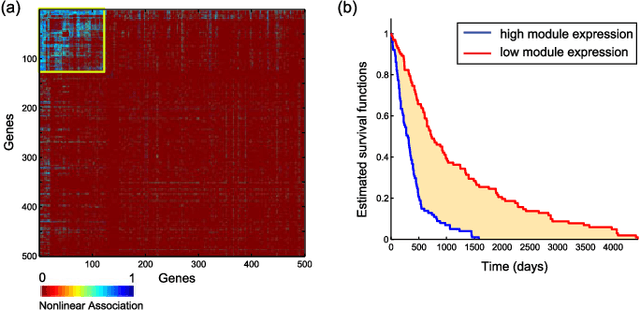
Abstract:We introduce Network Maximal Correlation (NMC) as a multivariate measure of nonlinear association among random variables. NMC is defined via an optimization that infers transformations of variables by maximizing aggregate inner products between transformed variables. For finite discrete and jointly Gaussian random variables, we characterize a solution of the NMC optimization using basis expansion of functions over appropriate basis functions. For finite discrete variables, we propose an algorithm based on alternating conditional expectation to determine NMC. Moreover we propose a distributed algorithm to compute an approximation of NMC for large and dense graphs using graph partitioning. For finite discrete variables, we show that the probability of discrepancy greater than any given level between NMC and NMC computed using empirical distributions decays exponentially fast as the sample size grows. For jointly Gaussian variables, we show that under some conditions the NMC optimization is an instance of the Max-Cut problem. We then illustrate an application of NMC in inference of graphical model for bijective functions of jointly Gaussian variables. Finally, we show NMC's utility in a data application of learning nonlinear dependencies among genes in a cancer dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge