Network Maximal Correlation
Paper and Code
Feb 09, 2017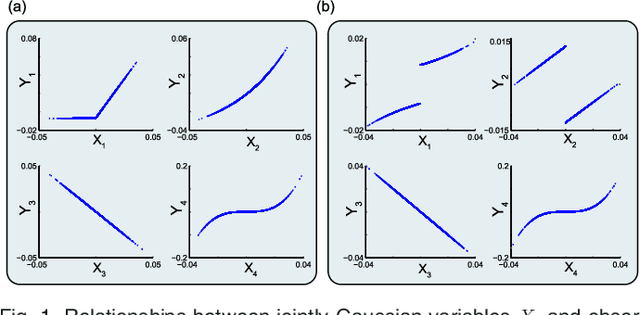
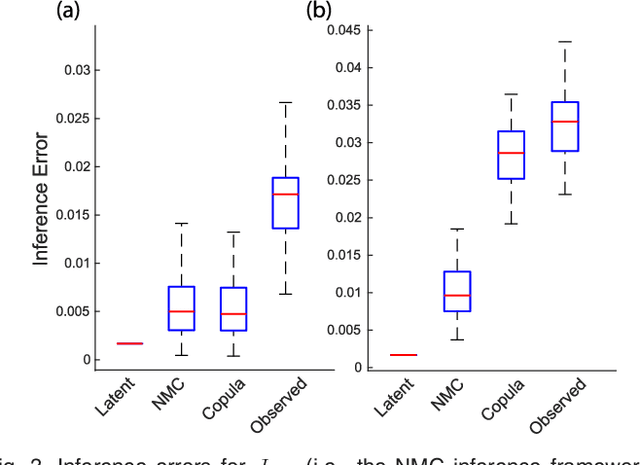
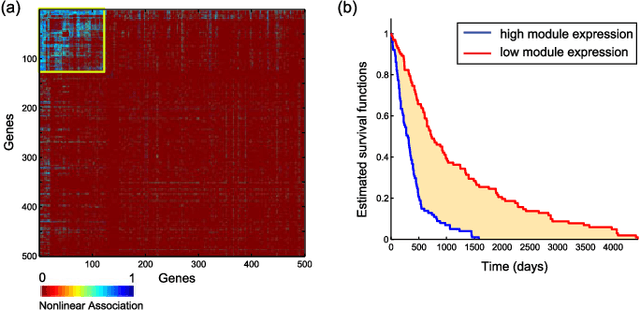
We introduce Network Maximal Correlation (NMC) as a multivariate measure of nonlinear association among random variables. NMC is defined via an optimization that infers transformations of variables by maximizing aggregate inner products between transformed variables. For finite discrete and jointly Gaussian random variables, we characterize a solution of the NMC optimization using basis expansion of functions over appropriate basis functions. For finite discrete variables, we propose an algorithm based on alternating conditional expectation to determine NMC. Moreover we propose a distributed algorithm to compute an approximation of NMC for large and dense graphs using graph partitioning. For finite discrete variables, we show that the probability of discrepancy greater than any given level between NMC and NMC computed using empirical distributions decays exponentially fast as the sample size grows. For jointly Gaussian variables, we show that under some conditions the NMC optimization is an instance of the Max-Cut problem. We then illustrate an application of NMC in inference of graphical model for bijective functions of jointly Gaussian variables. Finally, we show NMC's utility in a data application of learning nonlinear dependencies among genes in a cancer dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge