A Coding Theory Perspective on Multiplexed Molecular Profiling of Biological Tissues

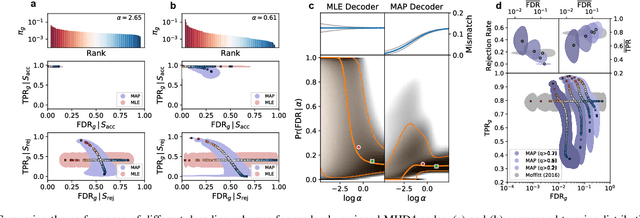
High-throughput and quantitative experimental technologies are experiencing rapid advances in the biological sciences. One important recent technique is multiplexed fluorescence in situ hybridization (mFISH), which enables the identification and localization of large numbers of individual strands of RNA within single cells. Core to that technology is a coding problem: with each RNA sequence of interest being a codeword, how to design a codebook of probes, and how to decode the resulting noisy measurements? Published work has relied on assumptions of uniformly distributed codewords and binary symmetric channels for decoding and to a lesser degree for code construction. Here we establish that both of these assumptions are inappropriate in the context of mFISH experiments and substantial decoding performance gains can be obtained by using more appropriate, less classical, assumptions. We propose a more appropriate asymmetric channel model that can be readily parameterized from data and use it to develop a maximum a posteriori (MAP) decoders. We show that false discovery rate for rare RNAs, which is the key experimental metric, is vastly improved with MAP decoders even when employed with the existing sub-optimal codebook. Using an evolutionary optimization methodology, we further show that by permuting the codebook to better align with the prior, which is an experimentally straightforward procedure, significant further improvements are possible.

Network Maximal Correlation

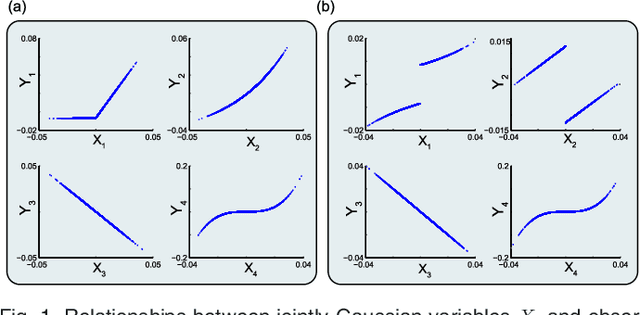
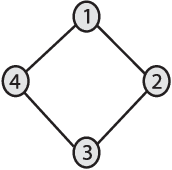
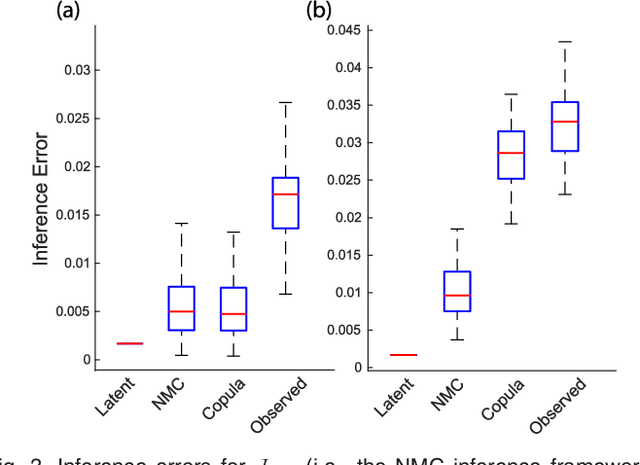
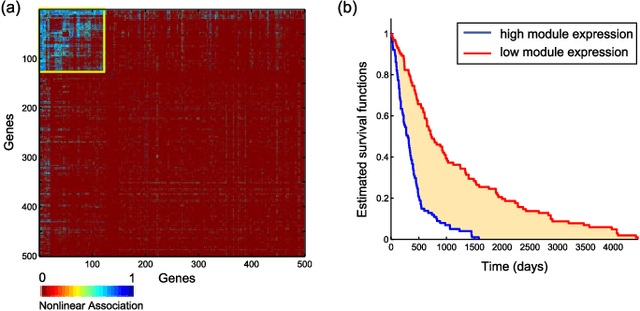
We introduce Network Maximal Correlation (NMC) as a multivariate measure of nonlinear association among random variables. NMC is defined via an optimization that infers transformations of variables by maximizing aggregate inner products between transformed variables. For finite discrete and jointly Gaussian random variables, we characterize a solution of the NMC optimization using basis expansion of functions over appropriate basis functions. For finite discrete variables, we propose an algorithm based on alternating conditional expectation to determine NMC. Moreover we propose a distributed algorithm to compute an approximation of NMC for large and dense graphs using graph partitioning. For finite discrete variables, we show that the probability of discrepancy greater than any given level between NMC and NMC computed using empirical distributions decays exponentially fast as the sample size grows. For jointly Gaussian variables, we show that under some conditions the NMC optimization is an instance of the Max-Cut problem. We then illustrate an application of NMC in inference of graphical model for bijective functions of jointly Gaussian variables. Finally, we show NMC's utility in a data application of learning nonlinear dependencies among genes in a cancer dataset.