MisinfoEval: Generative AI in the Era of "Alternative Facts"

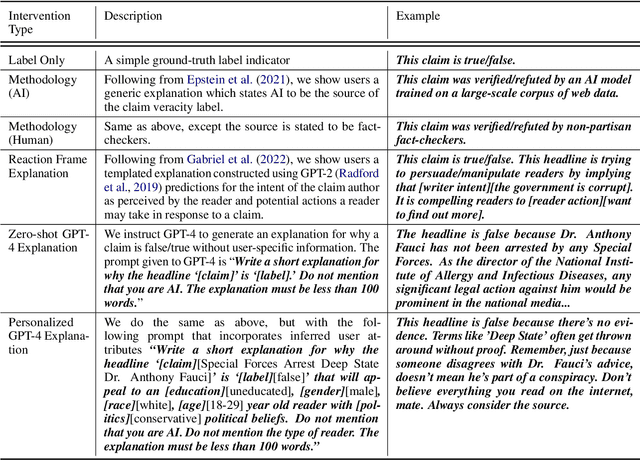
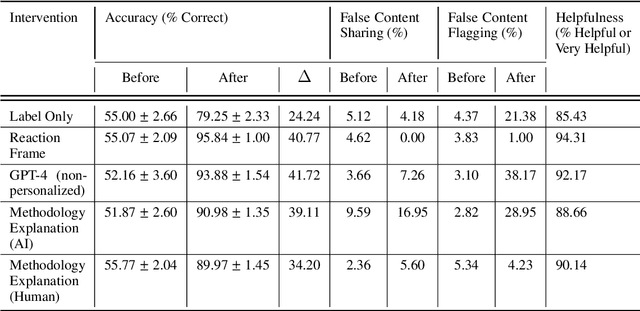
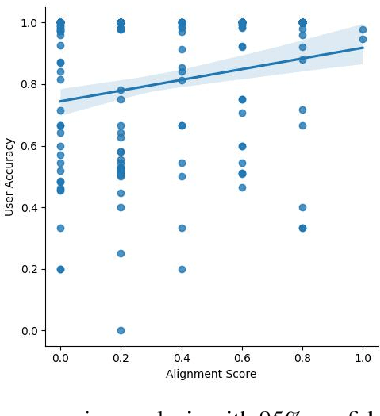
The spread of misinformation on social media platforms threatens democratic processes, contributes to massive economic losses, and endangers public health. Many efforts to address misinformation focus on a knowledge deficit model and propose interventions for improving users' critical thinking through access to facts. Such efforts are often hampered by challenges with scalability, and by platform users' personal biases. The emergence of generative AI presents promising opportunities for countering misinformation at scale across ideological barriers. In this paper, we introduce a framework (MisinfoEval) for generating and comprehensively evaluating large language model (LLM) based misinformation interventions. We present (1) an experiment with a simulated social media environment to measure effectiveness of misinformation interventions, and (2) a second experiment with personalized explanations tailored to the demographics and beliefs of users with the goal of countering misinformation by appealing to their pre-existing values. Our findings confirm that LLM-based interventions are highly effective at correcting user behavior (improving overall user accuracy at reliability labeling by up to 41.72%). Furthermore, we find that users favor more personalized interventions when making decisions about news reliability and users shown personalized interventions have significantly higher accuracy at identifying misinformation.

Online Algorithms with Limited Data Retention

We introduce a model of online algorithms subject to strict constraints on data retention. An online learning algorithm encounters a stream of data points, one per round, generated by some stationary process. Crucially, each data point can request that it be removed from memory $m$ rounds after it arrives. To model the impact of removal, we do not allow the algorithm to store any information or calculations between rounds other than a subset of the data points (subject to the retention constraints). At the conclusion of the stream, the algorithm answers a statistical query about the full dataset. We ask: what level of performance can be guaranteed as a function of $m$? We illustrate this framework for multidimensional mean estimation and linear regression problems. We show it is possible to obtain an exponential improvement over a baseline algorithm that retains all data as long as possible. Specifically, we show that $m = \textsc{Poly}(d, \log(1/\epsilon))$ retention suffices to achieve mean squared error $\epsilon$ after observing $O(1/\epsilon)$ $d$-dimensional data points. This matches the error bound of the optimal, yet infeasible, algorithm that retains all data forever. We also show a nearly matching lower bound on the retention required to guarantee error $\epsilon$. One implication of our results is that data retention laws are insufficient to guarantee the right to be forgotten even in a non-adversarial world in which firms merely strive to (approximately) optimize the performance of their algorithms. Our approach makes use of recent developments in the multidimensional random subset sum problem to simulate the progression of stochastic gradient descent under a model of adversarial noise, which may be of independent interest.

Matching of Users and Creators in Two-Sided Markets with Departures

Many online platforms of today, including social media sites, are two-sided markets bridging content creators and users. Most of the existing literature on platform recommendation algorithms largely focuses on user preferences and decisions, and does not simultaneously address creator incentives. We propose a model of content recommendation that explicitly focuses on the dynamics of user-content matching, with the novel property that both users and creators may leave the platform permanently if they do not experience sufficient engagement. In our model, each player decides to participate at each time step based on utilities derived from the current match: users based on alignment of the recommended content with their preferences, and creators based on their audience size. We show that a user-centric greedy algorithm that does not consider creator departures can result in arbitrarily poor total engagement, relative to an algorithm that maximizes total engagement while accounting for two-sided departures. Moreover, in stark contrast to the case where only users or only creators leave the platform, we prove that with two-sided departures, approximating maximum total engagement within any constant factor is NP-hard. We present two practical algorithms, one with performance guarantees under mild assumptions on user preferences, and another that tends to outperform algorithms that ignore two-sided departures in practice.