Integrated Hardware Architecture and Device Placement Search

Distributed execution of deep learning training involves a dynamic interplay between hardware accelerator architecture and device placement strategy. This is the first work to explore the co-optimization of determining the optimal architecture and device placement strategy through novel algorithms, improving the balance of computational resources, memory usage, and data distribution. Our architecture search leverages tensor and vector units, determining their quantity and dimensionality, and on-chip and off-chip memory configurations. It also determines the microbatch size and decides whether to recompute or stash activations, balancing the memory footprint of training and storage size. For each explored architecture configuration, we use an Integer Linear Program (ILP) to find the optimal schedule for executing operators on the accelerator. The ILP results then integrate with a dynamic programming solution to identify the most effective device placement strategy, combining data, pipeline, and tensor model parallelism across multiple accelerators. Our approach achieves higher throughput on large language models compared to the state-of-the-art TPUv4 and the Spotlight accelerator search framework. The entire source code of PHAZE is available at https://github.com/msr-fiddle/phaze.

Efficiently Computing Similarities to Private Datasets

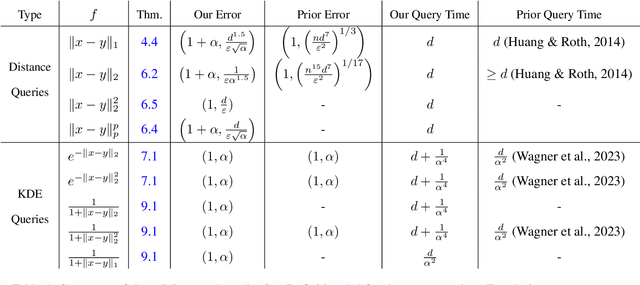
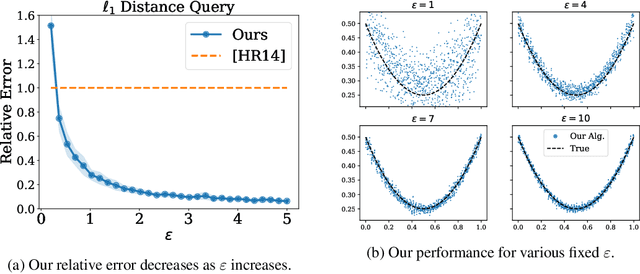
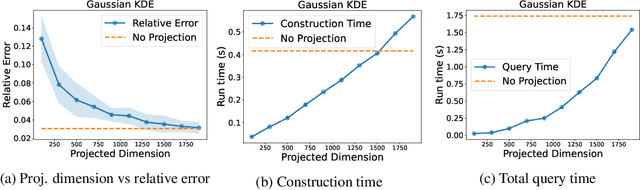
Many methods in differentially private model training rely on computing the similarity between a query point (such as public or synthetic data) and private data. We abstract out this common subroutine and study the following fundamental algorithmic problem: Given a similarity function $f$ and a large high-dimensional private dataset $X \subset \mathbb{R}^d$, output a differentially private (DP) data structure which approximates $\sum_{x \in X} f(x,y)$ for any query $y$. We consider the cases where $f$ is a kernel function, such as $f(x,y) = e^{-\|x-y\|_2^2/\sigma^2}$ (also known as DP kernel density estimation), or a distance function such as $f(x,y) = \|x-y\|_2$, among others. Our theoretical results improve upon prior work and give better privacy-utility trade-offs as well as faster query times for a wide range of kernels and distance functions. The unifying approach behind our results is leveraging `low-dimensional structures' present in the specific functions $f$ that we study, using tools such as provable dimensionality reduction, approximation theory, and one-dimensional decomposition of the functions. Our algorithms empirically exhibit improved query times and accuracy over prior state of the art. We also present an application to DP classification. Our experiments demonstrate that the simple methodology of classifying based on average similarity is orders of magnitude faster than prior DP-SGD based approaches for comparable accuracy.

Fairness in Submodular Maximization over a Matroid Constraint

Submodular maximization over a matroid constraint is a fundamental problem with various applications in machine learning. Some of these applications involve decision-making over datapoints with sensitive attributes such as gender or race. In such settings, it is crucial to guarantee that the selected solution is fairly distributed with respect to this attribute. Recently, fairness has been investigated in submodular maximization under a cardinality constraint in both the streaming and offline settings, however the more general problem with matroid constraint has only been considered in the streaming setting and only for monotone objectives. This work fills this gap. We propose various algorithms and impossibility results offering different trade-offs between quality, fairness, and generality.

Fairness in Streaming Submodular Maximization over a Matroid Constraint

Streaming submodular maximization is a natural model for the task of selecting a representative subset from a large-scale dataset. If datapoints have sensitive attributes such as gender or race, it becomes important to enforce fairness to avoid bias and discrimination. This has spurred significant interest in developing fair machine learning algorithms. Recently, such algorithms have been developed for monotone submodular maximization under a cardinality constraint. In this paper, we study the natural generalization of this problem to a matroid constraint. We give streaming algorithms as well as impossibility results that provide trade-offs between efficiency, quality and fairness. We validate our findings empirically on a range of well-known real-world applications: exemplar-based clustering, movie recommendation, and maximum coverage in social networks.

Near-Optimal Correlation Clustering with Privacy

Correlation clustering is a central problem in unsupervised learning, with applications spanning community detection, duplicate detection, automated labelling and many more. In the correlation clustering problem one receives as input a set of nodes and for each node a list of co-clustering preferences, and the goal is to output a clustering that minimizes the disagreement with the specified nodes' preferences. In this paper, we introduce a simple and computationally efficient algorithm for the correlation clustering problem with provable privacy guarantees. Our approximation guarantees are stronger than those shown in prior work and are optimal up to logarithmic factors.

Harmony: Overcoming the hurdles of GPU memory capacity to train massive DNN models on commodity servers

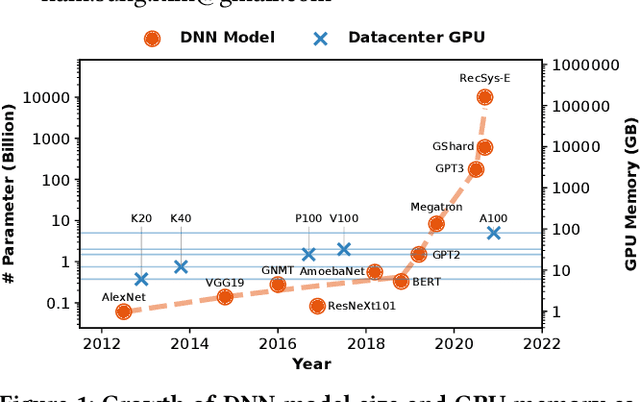
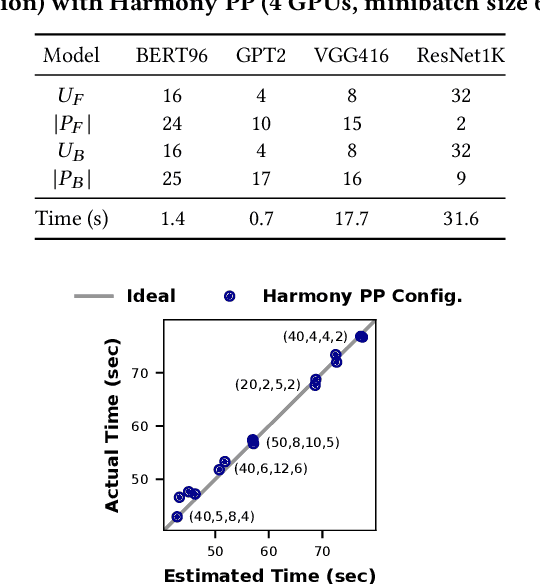
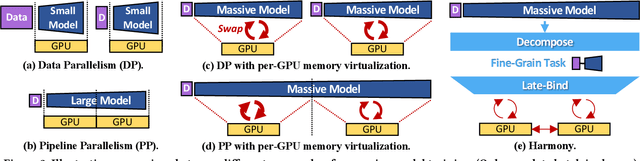
Deep neural networks (DNNs) have grown exponentially in complexity and size over the past decade, leaving only those who have access to massive datacenter-based resources with the ability to develop and train such models. One of the main challenges for the long tail of researchers who might have access to only limited resources (e.g., a single multi-GPU server) is limited GPU memory capacity compared to model size. The problem is so acute that the memory requirement of training large DNN models can often exceed the aggregate capacity of all available GPUs on commodity servers; this problem only gets worse with the trend of ever-growing model sizes. Current solutions that rely on virtualizing GPU memory (by swapping to/from CPU memory) incur excessive swapping overhead. In this paper, we present a new training framework, Harmony, and advocate rethinking how DNN frameworks schedule computation and move data to push the boundaries of training large models efficiently on modest multi-GPU deployments. Across many large DNN models, Harmony is able to reduce swap load by up to two orders of magnitude and obtain a training throughput speedup of up to 7.6x over highly optimized baselines with virtualized memory.

Correlation Clustering in Constant Many Parallel Rounds

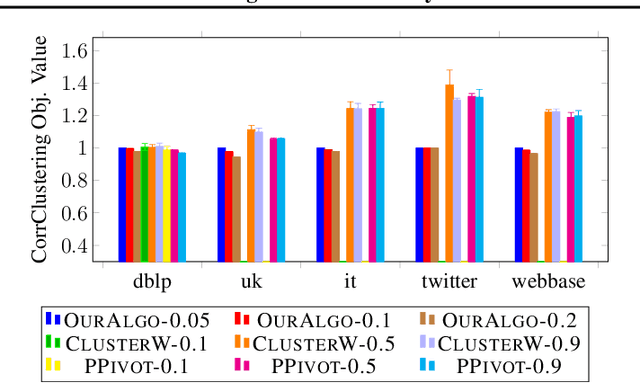
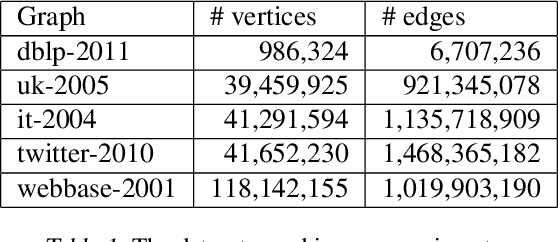
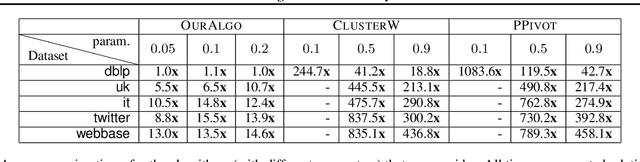
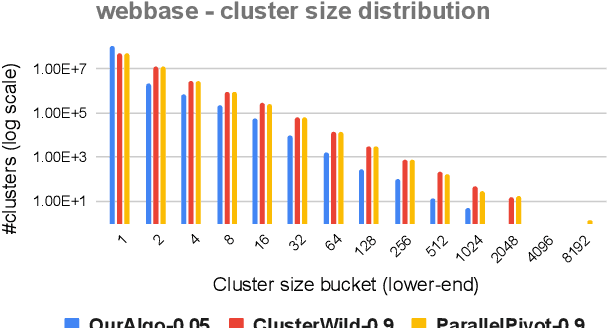
Correlation clustering is a central topic in unsupervised learning, with many applications in ML and data mining. In correlation clustering, one receives as input a signed graph and the goal is to partition it to minimize the number of disagreements. In this work we propose a massively parallel computation (MPC) algorithm for this problem that is considerably faster than prior work. In particular, our algorithm uses machines with memory sublinear in the number of nodes in the graph and returns a constant approximation while running only for a constant number of rounds. To the best of our knowledge, our algorithm is the first that can provably approximate a clustering problem on graphs using only a constant number of MPC rounds in the sublinear memory regime. We complement our analysis with an experimental analysis of our techniques.

Fairness in Streaming Submodular Maximization: Algorithms and Hardness

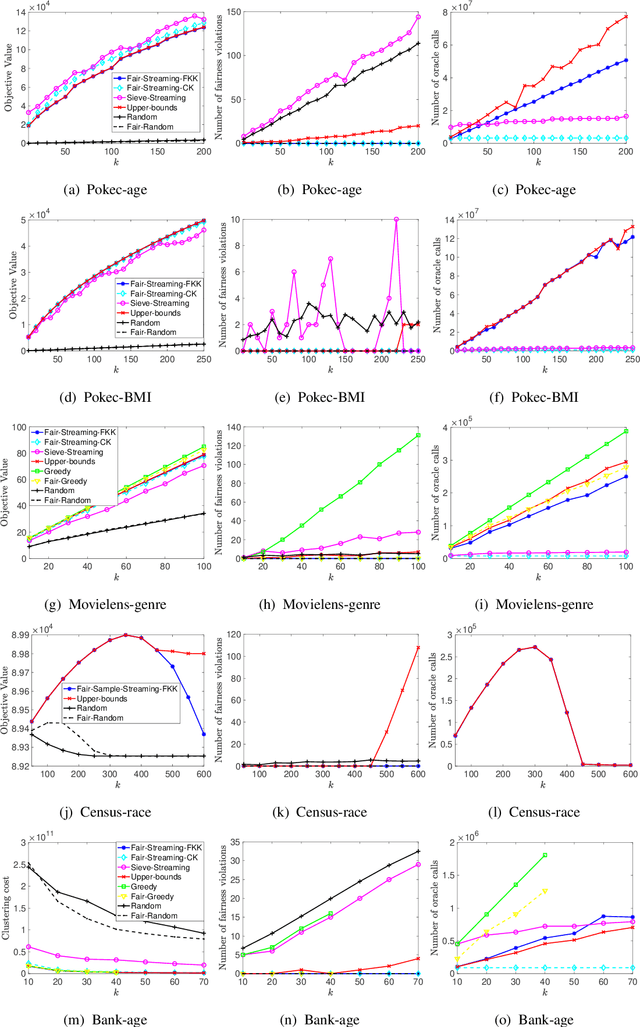
Submodular maximization has become established as the method of choice for the task of selecting representative and diverse summaries of data. However, if datapoints have sensitive attributes such as gender or age, such machine learning algorithms, left unchecked, are known to exhibit bias: under- or over-representation of particular groups. This has made the design of fair machine learning algorithms increasingly important. In this work we address the question: Is it possible to create fair summaries for massive datasets? To this end, we develop the first streaming approximation algorithms for submodular maximization under fairness constraints, for both monotone and non-monotone functions. We validate our findings empirically on exemplar-based clustering, movie recommendation, DPP-based summarization, and maximum coverage in social networks, showing that fairness constraints do not significantly impact utility.

Efficient Algorithms for Device Placement of DNN Graph Operators

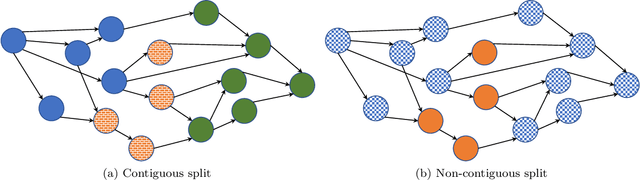
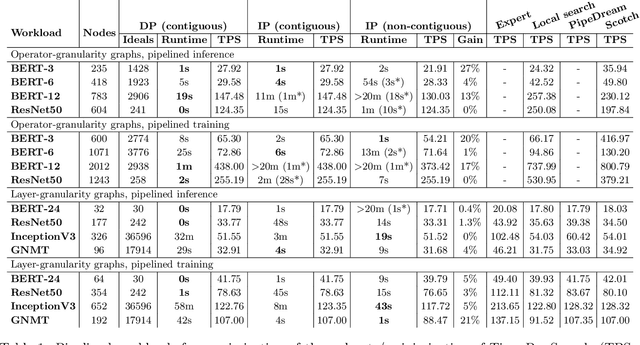
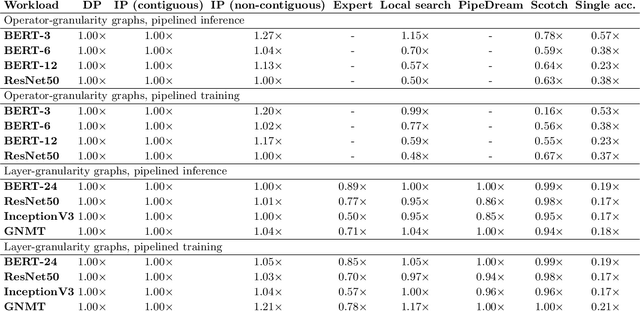
Modern machine learning workloads use large models, with complex structures, that are very expensive to execute. The devices that execute complex models are becoming increasingly heterogeneous as we see a flourishing of domain-specific accelerators being offered as hardware accelerators in addition to CPUs. These trends necessitate distributing the workload across multiple devices. Recent work has shown that significant gains can be obtained with model parallelism, i.e, partitioning a neural network's computational graph onto multiple devices. In particular, this form of parallelism assumes a pipeline of devices, which is fed a stream of samples and yields high throughput for training and inference of DNNs. However, for such settings (large models and multiple heterogeneous devices), we require automated algorithms and toolchains that can partition the ML workload across devices. In this paper, we identify and isolate the structured optimization problem at the core of device placement of DNN operators, for both inference and training, especially in modern pipelined settings. We then provide algorithms that solve this problem to optimality. We demonstrate the applicability and efficiency of our approaches using several contemporary DNN computation graphs.

Beyond $1/2$-Approximation for Submodular Maximization on Massive Data Streams

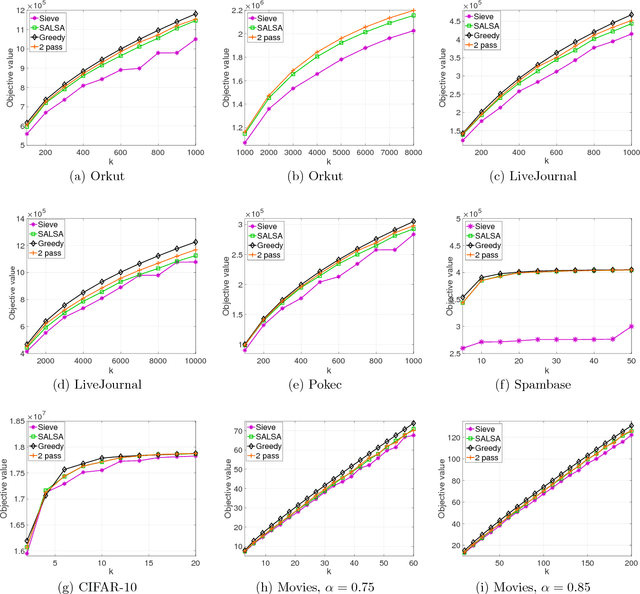
Many tasks in machine learning and data mining, such as data diversification, non-parametric learning, kernel machines, clustering etc., require extracting a small but representative summary from a massive dataset. Often, such problems can be posed as maximizing a submodular set function subject to a cardinality constraint. We consider this question in the streaming setting, where elements arrive over time at a fast pace and thus we need to design an efficient, low-memory algorithm. One such method, proposed by Badanidiyuru et al. (2014), always finds a $0.5$-approximate solution. Can this approximation factor be improved? We answer this question affirmatively by designing a new algorithm SALSA for streaming submodular maximization. It is the first low-memory, single-pass algorithm that improves the factor $0.5$, under the natural assumption that elements arrive in a random order. We also show that this assumption is necessary, i.e., that there is no such algorithm with better than $0.5$-approximation when elements arrive in arbitrary order. Our experiments demonstrate that SALSA significantly outperforms the state of the art in applications related to exemplar-based clustering, social graph analysis, and recommender systems.