Efficient Algorithms for Device Placement of DNN Graph Operators

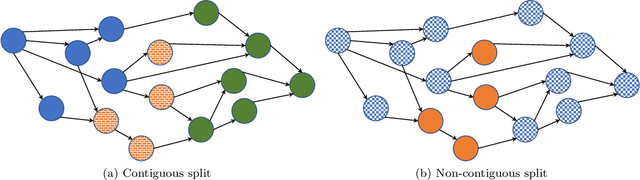
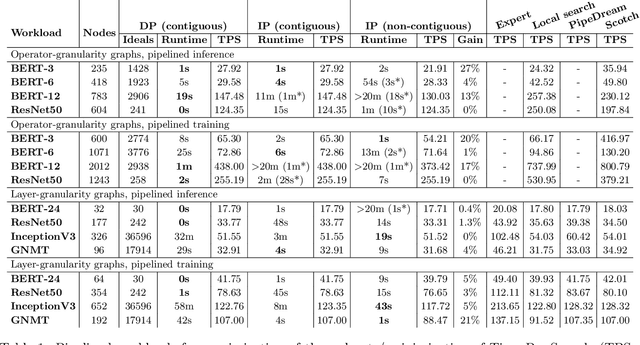
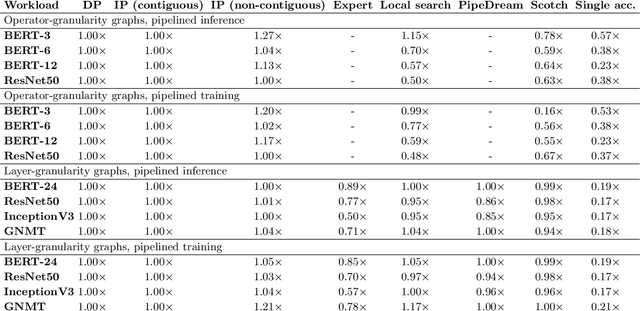
Modern machine learning workloads use large models, with complex structures, that are very expensive to execute. The devices that execute complex models are becoming increasingly heterogeneous as we see a flourishing of domain-specific accelerators being offered as hardware accelerators in addition to CPUs. These trends necessitate distributing the workload across multiple devices. Recent work has shown that significant gains can be obtained with model parallelism, i.e, partitioning a neural network's computational graph onto multiple devices. In particular, this form of parallelism assumes a pipeline of devices, which is fed a stream of samples and yields high throughput for training and inference of DNNs. However, for such settings (large models and multiple heterogeneous devices), we require automated algorithms and toolchains that can partition the ML workload across devices. In this paper, we identify and isolate the structured optimization problem at the core of device placement of DNN operators, for both inference and training, especially in modern pipelined settings. We then provide algorithms that solve this problem to optimality. We demonstrate the applicability and efficiency of our approaches using several contemporary DNN computation graphs.

Multi-scale Online Learning and its Applications to Online Auctions

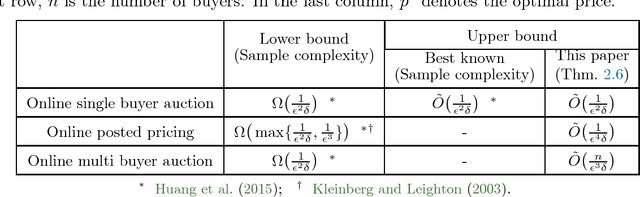
We consider revenue maximization in online auction/pricing problems. A seller sells an identical item in each period to a new buyer, or a new set of buyers. For the online posted pricing problem, we show regret bounds that scale with the best fixed price, rather than the range of the values. We also show regret bounds that are almost scale free, and match the offline sample complexity, when comparing to a benchmark that requires a lower bound on the market share. These results are obtained by generalizing the classical learning from experts and multi-armed bandit problems to their multi-scale versions. In this version, the reward of each action is in a different range, and the regret w.r.t. a given action scales with its own range, rather than the maximum range.

Linear Contextual Bandits with Knapsacks

We consider the linear contextual bandit problem with resource consumption, in addition to reward generation. In each round, the outcome of pulling an arm is a reward as well as a vector of resource consumptions. The expected values of these outcomes depend linearly on the context of that arm. The budget/capacity constraints require that the total consumption doesn't exceed the budget for each resource. The objective is once again to maximize the total reward. This problem turns out to be a common generalization of classic linear contextual bandits (linContextual), bandits with knapsacks (BwK), and the online stochastic packing problem (OSPP). We present algorithms with near-optimal regret bounds for this problem. Our bounds compare favorably to results on the unstructured version of the problem where the relation between the contexts and the outcomes could be arbitrary, but the algorithm only competes against a fixed set of policies accessible through an optimization oracle. We combine techniques from the work on linContextual, BwK, and OSPP in a nontrivial manner while also tackling new difficulties that are not present in any of these special cases.

An efficient algorithm for contextual bandits with knapsacks, and an extension to concave objectives

We consider a contextual version of multi-armed bandit problem with global knapsack constraints. In each round, the outcome of pulling an arm is a scalar reward and a resource consumption vector, both dependent on the context, and the global knapsack constraints require the total consumption for each resource to be below some pre-fixed budget. The learning agent competes with an arbitrary set of context-dependent policies. This problem was introduced by Badanidiyuru et al. (2014), who gave a computationally inefficient algorithm with near-optimal regret bounds for it. We give a computationally efficient algorithm for this problem with slightly better regret bounds, by generalizing the approach of Agarwal et al. (2014) for the non-constrained version of the problem. The computational time of our algorithm scales logarithmically in the size of the policy space. This answers the main open question of Badanidiyuru et al. (2014). We also extend our results to a variant where there are no knapsack constraints but the objective is an arbitrary Lipschitz concave function of the sum of outcome vectors.

Fast Algorithms for Online Stochastic Convex Programming

We introduce the online stochastic Convex Programming (CP) problem, a very general version of stochastic online problems which allows arbitrary concave objectives and convex feasibility constraints. Many well-studied problems like online stochastic packing and covering, online stochastic matching with concave returns, etc. form a special case of online stochastic CP. We present fast algorithms for these problems, which achieve near-optimal regret guarantees for both the i.i.d. and the random permutation models of stochastic inputs. When applied to the special case online packing, our ideas yield a simpler and faster primal-dual algorithm for this well studied problem, which achieves the optimal competitive ratio. Our techniques make explicit the connection of primal-dual paradigm and online learning to online stochastic CP.

Bandits with concave rewards and convex knapsacks

In this paper, we consider a very general model for exploration-exploitation tradeoff which allows arbitrary concave rewards and convex constraints on the decisions across time, in addition to the customary limitation on the time horizon. This model subsumes the classic multi-armed bandit (MAB) model, and the Bandits with Knapsacks (BwK) model of Badanidiyuru et al.[2013]. We also consider an extension of this model to allow linear contexts, similar to the linear contextual extension of the MAB model. We demonstrate that a natural and simple extension of the UCB family of algorithms for MAB provides a polynomial time algorithm that has near-optimal regret guarantees for this substantially more general model, and matches the bounds provided by Badanidiyuru et al.[2013] for the special case of BwK, which is quite surprising. We also provide computationally more efficient algorithms by establishing interesting connections between this problem and other well studied problems/algorithms such as the Blackwell approachability problem, online convex optimization, and the Frank-Wolfe technique for convex optimization. We give examples of several concrete applications, where this more general model of bandits allows for richer and/or more efficient formulations of the problem.