Lihong Li
HeaPA: Difficulty-Aware Heap Sampling and On-Policy Query Augmentation for LLM Reinforcement Learning
Jan 30, 2026Abstract:RLVR is now a standard way to train LLMs on reasoning tasks with verifiable outcomes, but when rollout generation dominates the cost, efficiency depends heavily on which prompts you sample and when. In practice, prompt pools are often static or only loosely tied to the model's learning progress, so uniform sampling can't keep up with the shifting capability frontier and ends up wasting rollouts on prompts that are already solved or still out of reach. Existing approaches improve efficiency through filtering, curricula, adaptive rollout allocation, or teacher guidance, but they typically assume a fixed pool-which makes it hard to support stable on-policy pool growth-or they add extra teacher cost and latency. We introduce HeaPA (Heap Sampling and On-Policy Query Augmentation), which maintains a bounded, evolving pool, tracks the frontier using heap-based boundary sampling, expands the pool via on-policy augmentation with lightweight asynchronous validation, and stabilizes correlated queries through topology-aware re-estimation of pool statistics and controlled reinsertion. Across two training corpora, two training recipes, and seven benchmarks, HeaPA consistently improves accuracy and reaches target performance with fewer computations while keeping wall-clock time comparable. Our analyses suggest these gains come from frontier-focused sampling and on-policy pool growth, with the benefits becoming larger as model scale increases. Our code is available at https://github.com/horizon-rl/HeaPA.
Turn-PPO: Turn-Level Advantage Estimation with PPO for Improved Multi-Turn RL in Agentic LLMs
Dec 18, 2025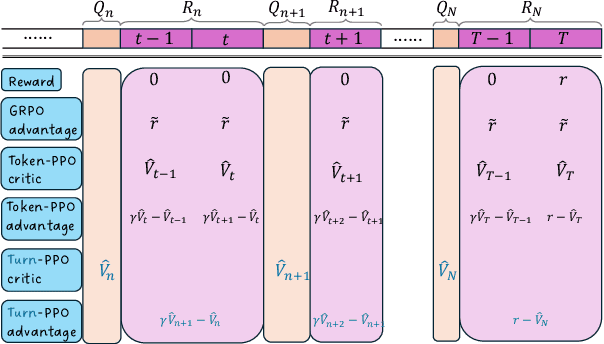

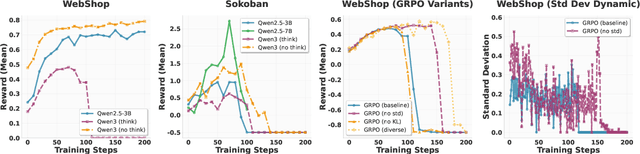
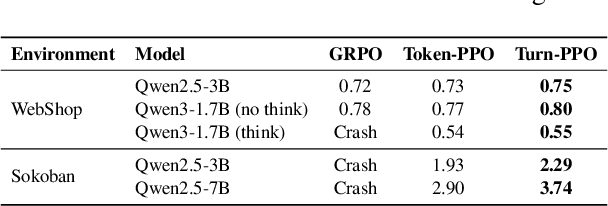
Abstract:Reinforcement learning (RL) has re-emerged as a natural approach for training interactive LLM agents in real-world environments. However, directly applying the widely used Group Relative Policy Optimization (GRPO) algorithm to multi-turn tasks exposes notable limitations, particularly in scenarios requiring long-horizon reasoning. To address these challenges, we investigate more stable and effective advantage estimation strategies, especially for multi-turn settings. We first explore Proximal Policy Optimization (PPO) as an alternative and find it to be more robust than GRPO. To further enhance PPO in multi-turn scenarios, we introduce turn-PPO, a variant that operates on a turn-level MDP formulation, as opposed to the commonly used token-level MDP. Our results on the WebShop and Sokoban datasets demonstrate the effectiveness of turn-PPO, both with and without long reasoning components.
Ask a Strong LLM Judge when Your Reward Model is Uncertain
Oct 23, 2025Abstract:Reward model (RM) plays a pivotal role in reinforcement learning with human feedback (RLHF) for aligning large language models (LLMs). However, classical RMs trained on human preferences are vulnerable to reward hacking and generalize poorly to out-of-distribution (OOD) inputs. By contrast, strong LLM judges equipped with reasoning capabilities demonstrate superior generalization, even without additional training, but incur significantly higher inference costs, limiting their applicability in online RLHF. In this work, we propose an uncertainty-based routing framework that efficiently complements a fast RM with a strong but costly LLM judge. Our approach formulates advantage estimation in policy gradient (PG) methods as pairwise preference classification, enabling principled uncertainty quantification to guide routing. Uncertain pairs are forwarded to the LLM judge, while confident ones are evaluated by the RM. Experiments on RM benchmarks demonstrate that our uncertainty-based routing strategy significantly outperforms random judge calling at the same cost, and downstream alignment results showcase its effectiveness in improving online RLHF.
WebAgent-R1: Training Web Agents via End-to-End Multi-Turn Reinforcement Learning
May 22, 2025Abstract:While reinforcement learning (RL) has demonstrated remarkable success in enhancing large language models (LLMs), it has primarily focused on single-turn tasks such as solving math problems. Training effective web agents for multi-turn interactions remains challenging due to the complexity of long-horizon decision-making across dynamic web interfaces. In this work, we present WebAgent-R1, a simple yet effective end-to-end multi-turn RL framework for training web agents. It learns directly from online interactions with web environments by asynchronously generating diverse trajectories, entirely guided by binary rewards depending on task success. Experiments on the WebArena-Lite benchmark demonstrate the effectiveness of WebAgent-R1, boosting the task success rate of Qwen-2.5-3B from 6.1% to 33.9% and Llama-3.1-8B from 8.5% to 44.8%, significantly outperforming existing state-of-the-art methods and strong proprietary models such as OpenAI o3. In-depth analyses reveal the effectiveness of the thinking-based prompting strategy and test-time scaling through increased interactions for web tasks. We further investigate different RL initialization policies by introducing two variants, namely WebAgent-R1-Zero and WebAgent-R1-CoT, which highlight the importance of the warm-up training stage (i.e., behavior cloning) and provide insights on incorporating long chain-of-thought (CoT) reasoning in web agents.
MESOB: Balancing Equilibria & Social Optimality
Jul 16, 2023Abstract:Motivated by bid recommendation in online ad auctions, this paper considers a general class of multi-level and multi-agent games, with two major characteristics: one is a large number of anonymous agents, and the other is the intricate interplay between competition and cooperation. To model such complex systems, we propose a novel and tractable bi-objective optimization formulation with mean-field approximation, called MESOB (Mean-field Equilibria & Social Optimality Balancing), as well as an associated occupation measure optimization (OMO) method called MESOB-OMO to solve it. MESOB-OMO enables obtaining approximately Pareto efficient solutions in terms of the dual objectives of competition and cooperation in MESOB, and in particular allows for Nash equilibrium selection and social equalization in an asymptotic manner. We apply MESOB-OMO to bid recommendation in a simulated pay-per-click ad auction. Experiments demonstrate its efficacy in balancing the interests of different parties and in handling the competitive nature of bidders, as well as its advantages over baselines that only consider either the competitive or the cooperative aspects.
Offline Policy Optimization in RL with Variance Regularizaton
Dec 29, 2022



Abstract:Learning policies from fixed offline datasets is a key challenge to scale up reinforcement learning (RL) algorithms towards practical applications. This is often because off-policy RL algorithms suffer from distributional shift, due to mismatch between dataset and the target policy, leading to high variance and over-estimation of value functions. In this work, we propose variance regularization for offline RL algorithms, using stationary distribution corrections. We show that by using Fenchel duality, we can avoid double sampling issues for computing the gradient of the variance regularizer. The proposed algorithm for offline variance regularization (OVAR) can be used to augment any existing offline policy optimization algorithms. We show that the regularizer leads to a lower bound to the offline policy optimization objective, which can help avoid over-estimation errors, and explains the benefits of our approach across a range of continuous control domains when compared to existing state-of-the-art algorithms.
A Reinforcement Learning Approach to Estimating Long-term Treatment Effects
Oct 14, 2022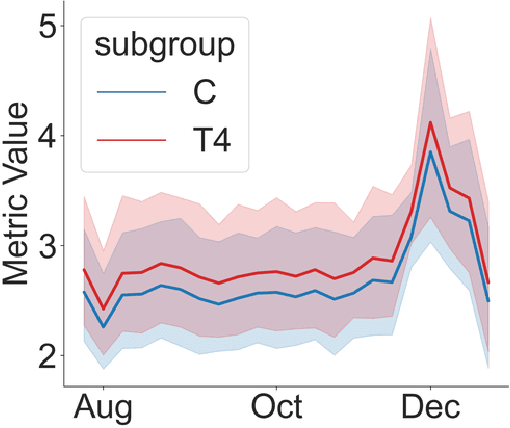

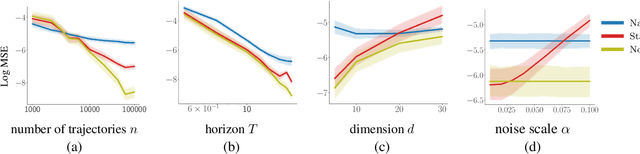
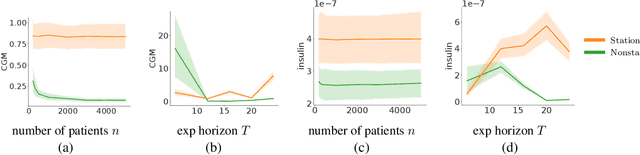
Abstract:Randomized experiments (a.k.a. A/B tests) are a powerful tool for estimating treatment effects, to inform decisions making in business, healthcare and other applications. In many problems, the treatment has a lasting effect that evolves over time. A limitation with randomized experiments is that they do not easily extend to measure long-term effects, since running long experiments is time-consuming and expensive. In this paper, we take a reinforcement learning (RL) approach that estimates the average reward in a Markov process. Motivated by real-world scenarios where the observed state transition is nonstationary, we develop a new algorithm for a class of nonstationary problems, and demonstrate promising results in two synthetic datasets and one online store dataset.
Understanding Domain Randomization for Sim-to-real Transfer
Oct 07, 2021
Abstract:Reinforcement learning encounters many challenges when applied directly in the real world. Sim-to-real transfer is widely used to transfer the knowledge learned from simulation to the real world. Domain randomization -- one of the most popular algorithms for sim-to-real transfer -- has been demonstrated to be effective in various tasks in robotics and autonomous driving. Despite its empirical successes, theoretical understanding on why this simple algorithm works is limited. In this paper, we propose a theoretical framework for sim-to-real transfers, in which the simulator is modeled as a set of MDPs with tunable parameters (corresponding to unknown physical parameters such as friction). We provide sharp bounds on the sim-to-real gap -- the difference between the value of policy returned by domain randomization and the value of an optimal policy for the real world. We prove that sim-to-real transfer can succeed under mild conditions without any real-world training samples. Our theory also highlights the importance of using memory (i.e., history-dependent policies) in domain randomization. Our proof is based on novel techniques that reduce the problem of bounding the sim-to-real gap to the problem of designing efficient learning algorithms for infinite-horizon MDPs, which we believe are of independent interest.
A Map of Bandits for E-commerce
Jul 01, 2021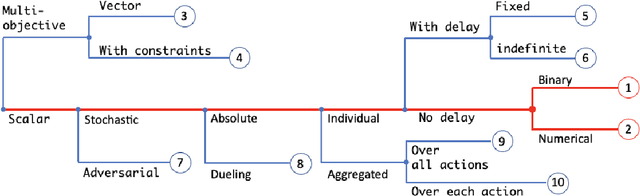

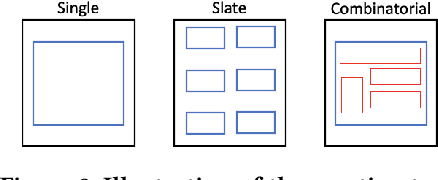
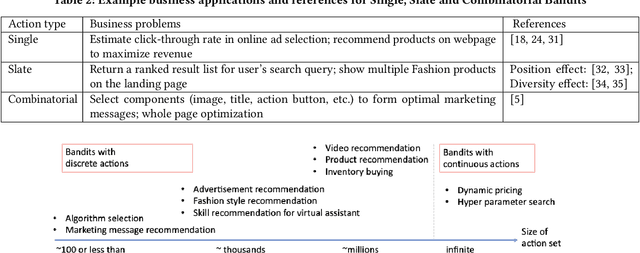
Abstract:The rich body of Bandit literature not only offers a diverse toolbox of algorithms, but also makes it hard for a practitioner to find the right solution to solve the problem at hand. Typical textbooks on Bandits focus on designing and analyzing algorithms, and surveys on applications often present a list of individual applications. While these are valuable resources, there exists a gap in mapping applications to appropriate Bandit algorithms. In this paper, we aim to reduce this gap with a structured map of Bandits to help practitioners navigate to find relevant and practical Bandit algorithms. Instead of providing a comprehensive overview, we focus on a small number of key decision points related to reward, action, and features, which often affect how Bandit algorithms are chosen in practice.
On the Optimality of Batch Policy Optimization Algorithms
Apr 06, 2021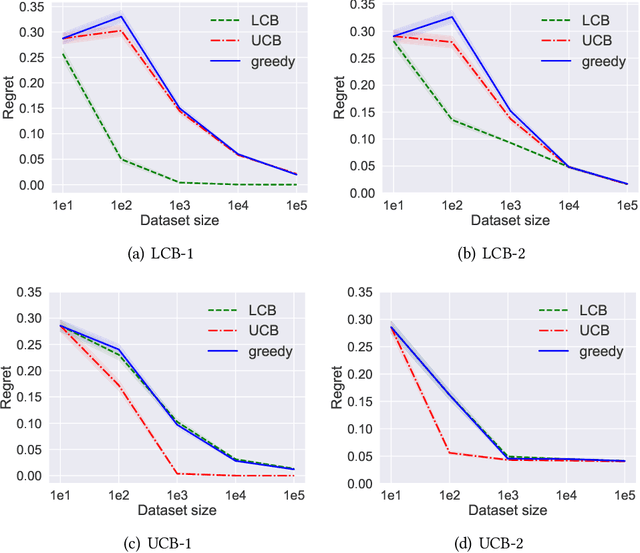
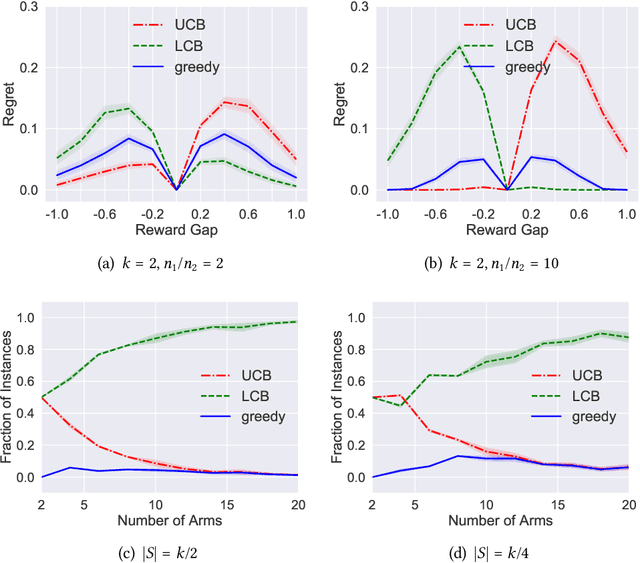
Abstract:Batch policy optimization considers leveraging existing data for policy construction before interacting with an environment. Although interest in this problem has grown significantly in recent years, its theoretical foundations remain under-developed. To advance the understanding of this problem, we provide three results that characterize the limits and possibilities of batch policy optimization in the finite-armed stochastic bandit setting. First, we introduce a class of confidence-adjusted index algorithms that unifies optimistic and pessimistic principles in a common framework, which enables a general analysis. For this family, we show that any confidence-adjusted index algorithm is minimax optimal, whether it be optimistic, pessimistic or neutral. Our analysis reveals that instance-dependent optimality, commonly used to establish optimality of on-line stochastic bandit algorithms, cannot be achieved by any algorithm in the batch setting. In particular, for any algorithm that performs optimally in some environment, there exists another environment where the same algorithm suffers arbitrarily larger regret. Therefore, to establish a framework for distinguishing algorithms, we introduce a new weighted-minimax criterion that considers the inherent difficulty of optimal value prediction. We demonstrate how this criterion can be used to justify commonly used pessimistic principles for batch policy optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge