CoinDICE: Off-Policy Confidence Interval Estimation
Paper and Code
Oct 22, 2020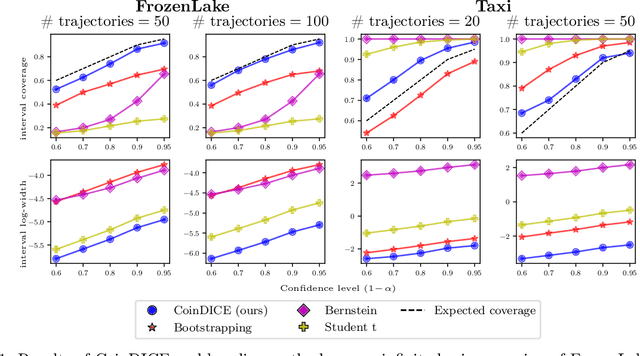
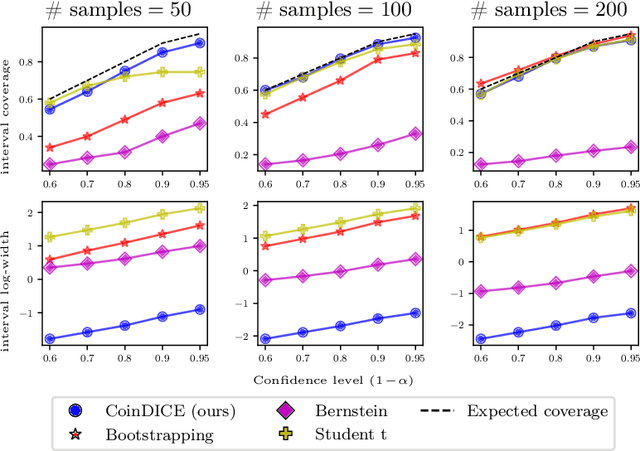
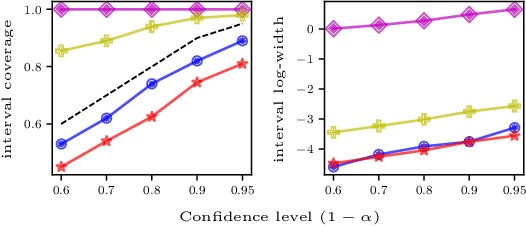
We study high-confidence behavior-agnostic off-policy evaluation in reinforcement learning, where the goal is to estimate a confidence interval on a target policy's value, given only access to a static experience dataset collected by unknown behavior policies. Starting from a function space embedding of the linear program formulation of the $Q$-function, we obtain an optimization problem with generalized estimating equation constraints. By applying the generalized empirical likelihood method to the resulting Lagrangian, we propose CoinDICE, a novel and efficient algorithm for computing confidence intervals. Theoretically, we prove the obtained confidence intervals are valid, in both asymptotic and finite-sample regimes. Empirically, we show in a variety of benchmarks that the confidence interval estimates are tighter and more accurate than existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge