MF-OML: Online Mean-Field Reinforcement Learning with Occupation Measures for Large Population Games

Reinforcement learning for multi-agent games has attracted lots of attention recently. However, given the challenge of solving Nash equilibria for large population games, existing works with guaranteed polynomial complexities either focus on variants of zero-sum and potential games, or aim at solving (coarse) correlated equilibria, or require access to simulators, or rely on certain assumptions that are hard to verify. This work proposes MF-OML (Mean-Field Occupation-Measure Learning), an online mean-field reinforcement learning algorithm for computing approximate Nash equilibria of large population sequential symmetric games. MF-OML is the first fully polynomial multi-agent reinforcement learning algorithm for provably solving Nash equilibria (up to mean-field approximation gaps that vanish as the number of players $N$ goes to infinity) beyond variants of zero-sum and potential games. When evaluated by the cumulative deviation from Nash equilibria, the algorithm is shown to achieve a high probability regret bound of $\tilde{O}(M^{3/4}+N^{-1/2}M)$ for games with the strong Lasry-Lions monotonicity condition, and a regret bound of $\tilde{O}(M^{11/12}+N^{- 1/6}M)$ for games with only the Lasry-Lions monotonicity condition, where $M$ is the total number of episodes and $N$ is the number of agents of the game. As a byproduct, we also obtain the first tractable globally convergent computational algorithm for computing approximate Nash equilibria of monotone mean-field games.

MESOB: Balancing Equilibria & Social Optimality

Motivated by bid recommendation in online ad auctions, this paper considers a general class of multi-level and multi-agent games, with two major characteristics: one is a large number of anonymous agents, and the other is the intricate interplay between competition and cooperation. To model such complex systems, we propose a novel and tractable bi-objective optimization formulation with mean-field approximation, called MESOB (Mean-field Equilibria & Social Optimality Balancing), as well as an associated occupation measure optimization (OMO) method called MESOB-OMO to solve it. MESOB-OMO enables obtaining approximately Pareto efficient solutions in terms of the dual objectives of competition and cooperation in MESOB, and in particular allows for Nash equilibrium selection and social equalization in an asymptotic manner. We apply MESOB-OMO to bid recommendation in a simulated pay-per-click ad auction. Experiments demonstrate its efficacy in balancing the interests of different parties and in handling the competitive nature of bidders, as well as its advantages over baselines that only consider either the competitive or the cooperative aspects.

Joint Graph Learning and Model Fitting in Laplacian Regularized Stratified Models

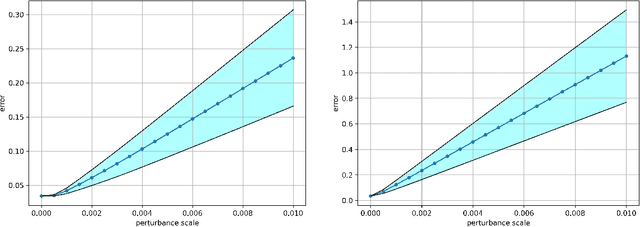
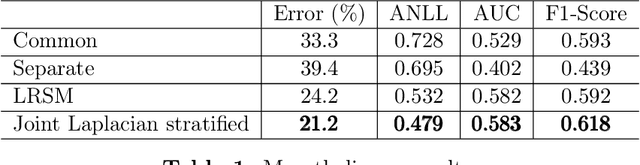
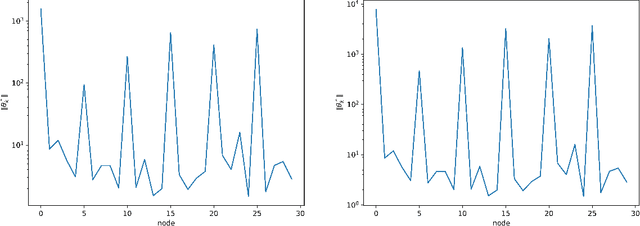
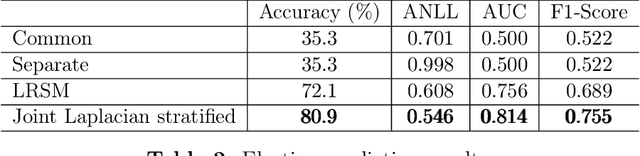
Laplacian regularized stratified models (LRSM) are models that utilize the explicit or implicit network structure of the sub-problems as defined by the categorical features called strata (e.g., age, region, time, forecast horizon, etc.), and draw upon data from neighboring strata to enhance the parameter learning of each sub-problem. They have been widely applied in machine learning and signal processing problems, including but not limited to time series forecasting, representation learning, graph clustering, max-margin classification, and general few-shot learning. Nevertheless, existing works on LRSM have either assumed a known graph or are restricted to specific applications. In this paper, we start by showing the importance and sensitivity of graph weights in LRSM, and provably show that the sensitivity can be arbitrarily large when the parameter scales and sample sizes are heavily imbalanced across nodes. We then propose a generic approach to jointly learn the graph while fitting the model parameters by solving a single optimization problem. We interpret the proposed formulation from both a graph connectivity viewpoint and an end-to-end Bayesian perspective, and propose an efficient algorithm to solve the problem. Convergence guarantees of the proposed optimization algorithm is also provided despite the lack of global strongly smoothness of the Laplacian regularization term typically required in the existing literature, which may be of independent interest. Finally, we illustrate the efficiency of our approach compared to existing methods by various real-world numerical examples.

Beyond Exact Gradients: Convergence of Stochastic Soft-Max Policy Gradient Methods with Entropy Regularization

Entropy regularization is an efficient technique for encouraging exploration and preventing a premature convergence of (vanilla) policy gradient methods in reinforcement learning (RL). However, the theoretical understanding of entropy regularized RL algorithms has been limited. In this paper, we revisit the classical entropy regularized policy gradient methods with the soft-max policy parametrization, whose convergence has so far only been established assuming access to exact gradient oracles. To go beyond this scenario, we propose the first set of (nearly) unbiased stochastic policy gradient estimators with trajectory-level entropy regularization, with one being an unbiased visitation measure-based estimator and the other one being a nearly unbiased yet more practical trajectory-based estimator. We prove that although the estimators themselves are unbounded in general due to the additional logarithmic policy rewards introduced by the entropy term, the variances are uniformly bounded. This enables the development of the first set of convergence results for stochastic entropy regularized policy gradient methods to both stationary points and globally optimal policies. We also develop some improved sample complexity results under a good initialization.

On the Global Convergence of Momentum-based Policy Gradient

Policy gradient (PG) methods are popular and efficient for large-scale reinforcement learning due to their relative stability and incremental nature. In recent years, the empirical success of PG methods has led to the development of a theoretical foundation for these methods. In this work, we generalize this line of research by studying the global convergence of stochastic PG methods with momentum terms, which have been demonstrated to be efficient recipes for improving PG methods. We study both the soft-max and the Fisher-non-degenerate policy parametrizations, and show that adding a momentum improves the global optimality sample complexity of vanilla PG methods by $\tilde{\mathcal{O}}(\epsilon^{-1.5})$ and $\tilde{\mathcal{O}}(\epsilon^{-1})$, respectively, where $\epsilon>0$ is the target tolerance. Our work is the first one that obtains global convergence results for the momentum-based PG methods. For the generic Fisher-non-degenerate policy parametrizations, our result is the first single-loop and finite-batch PG algorithm achieving $\tilde{O}(\epsilon^{-3})$ global optimality sample complexity. Finally, as a by-product, our methods also provide general framework for analyzing the global convergence rates of stochastic PG methods, which can be easily applied and extended to different PG estimators.

Theoretical Guarantees of Fictitious Discount Algorithms for Episodic Reinforcement Learning and Global Convergence of Policy Gradient Methods

When designing algorithms for finite-time-horizon episodic reinforcement learning problems, a common approach is to introduce a fictitious discount factor and use stationary policies for approximations. Empirically, it has been shown that the fictitious discount factor helps reduce variance, and stationary policies serve to save the per-iteration computational cost. Theoretically, however, there is no existing work on convergence analysis for algorithms with this fictitious discount recipe. This paper takes the first step towards analyzing these algorithms. It focuses on two vanilla policy gradient (VPG) variants: the first being a widely used variant with discounted advantage estimations (DAE), the second with an additional fictitious discount factor in the score functions of the policy gradient estimators. Non-asymptotic convergence guarantees are established for both algorithms, and the additional discount factor is shown to reduce the bias introduced in DAE and thus improve the algorithm convergence asymptotically. A key ingredient of our analysis is to connect three settings of Markov decision processes (MDPs): the finite-time-horizon, the average reward and the discounted settings. To our best knowledge, this is the first theoretical guarantee on fictitious discount algorithms for the episodic reinforcement learning of finite-time-horizon MDPs, which also leads to the (first) global convergence of policy gradient methods for finite-time-horizon episodic reinforcement learning.

Sample Efficient Reinforcement Learning with REINFORCE

Policy gradient methods are among the most effective methods for large-scale reinforcement learning, and their empirical success has prompted several works that develop the foundation of their global convergence theory. However, prior works have either required exact gradients or state-action visitation measure based mini-batch stochastic gradients with a diverging batch size, which limit their applicability in practical scenarios. In this paper, we consider classical policy gradient methods that compute an approximate gradient with a single trajectory or a fixed size mini-batch of trajectories, along with the widely-used REINFORCE gradient estimation procedure. By controlling the number of "bad" episodes and resorting to the classical doubling trick, we establish an anytime sub-linear high probability regret bound as well as almost sure global convergence of the average regret with an asymptotically sub-linear rate. These provide the first set of global convergence and sample efficiency results for the well-known REINFORCE algorithm and contribute to a better understanding of its performance in practice.

A General Framework for Learning Mean-Field Games

This paper presents a general mean-field game (GMFG) framework for simultaneous learning and decision-making in stochastic games with a large population. It first establishes the existence of a unique Nash Equilibrium to this GMFG, and demonstrates that naively combining Q-learning with the fixed-point approach in classical MFGs yields unstable algorithms. It then proposes value-based and policy-based reinforcement learning algorithms (GMF-P and GMF-P respectively) with smoothed policies, with analysis of convergence property and computational complexity. The experiments on repeated Ad auction problems demonstrate that GMF-V-Q, a specific GMF-V algorithm based on Q-learning, is efficient and robust in terms of convergence and learning accuracy. Moreover, its performance is superior in convergence, stability, and learning ability, when compared with existing algorithms for multi-agent reinforcement learning.

Robust Super-Level Set Estimation using Gaussian Processes

This paper focuses on the problem of determining as large a region as possible where a function exceeds a given threshold with high probability. We assume that we only have access to a noise-corrupted version of the function and that function evaluations are costly. To select the next query point, we propose maximizing the expected volume of the domain identified as above the threshold as predicted by a Gaussian process, robustified by a variance term. We also give asymptotic guarantees on the exploration effect of the algorithm, regardless of the prior misspecification. We show by various numerical examples that our approach also outperforms existing techniques in the literature in practice.