High Probability Complexity Bounds of Trust-Region Stochastic Sequential Quadratic Programming with Heavy-Tailed Noise

In this paper, we consider nonlinear optimization problems with a stochastic objective and deterministic equality constraints. We propose a Trust-Region Stochastic Sequential Quadratic Programming (TR-SSQP) method and establish its high-probability iteration complexity bounds for identifying first- and second-order $\epsilon$-stationary points. In our algorithm, we assume that exact objective values, gradients, and Hessians are not directly accessible but can be estimated via zeroth-, first-, and second-order probabilistic oracles. Compared to existing complexity studies of SSQP methods that rely on a zeroth-order oracle with sub-exponential tail noise (i.e., light-tailed) and focus mostly on first-order stationarity, our analysis accommodates irreducible and heavy-tailed noise in the zeroth-order oracle and significantly extends the analysis to second-order stationarity. We show that under weaker noise conditions, our method achieves the same high-probability first-order iteration complexity bounds, while also exhibiting promising second-order iteration complexity bounds. Specifically, the method identifies a first-order $\epsilon$-stationary point in $\mathcal{O}(\epsilon^{-2})$ iterations and a second-order $\epsilon$-stationary point in $\mathcal{O}(\epsilon^{-3})$ iterations with high probability, provided that $\epsilon$ is lower bounded by a constant determined by the irreducible noise level in estimation. We validate our theoretical findings and evaluate the practical performance of our method on CUTEst benchmark test set.

Subgradient Method for System Identification with Non-Smooth Objectives

This paper investigates a subgradient-based algorithm to solve the system identification problem for linear time-invariant systems with non-smooth objectives. This is essential for robust system identification in safety-critical applications. While existing work provides theoretical exact recovery guarantees using optimization solvers, the design of fast learning algorithms with convergence guarantees for practical use remains unexplored. We analyze the subgradient method in this setting where the optimization problems to be solved change over time as new measurements are taken, and we establish linear convergence results for both the best and Polyak step sizes after a burn-in period. Additionally, we characterize the asymptotic convergence of the best average sub-optimality gap under diminishing and constant step sizes. Finally, we compare the time complexity of standard solvers with the subgradient algorithm and support our findings with experimental results. This is the first work to analyze subgradient algorithms for system identification with non-smooth objectives.

Reward-Safety Balance in Offline Safe RL via Diffusion Regularization

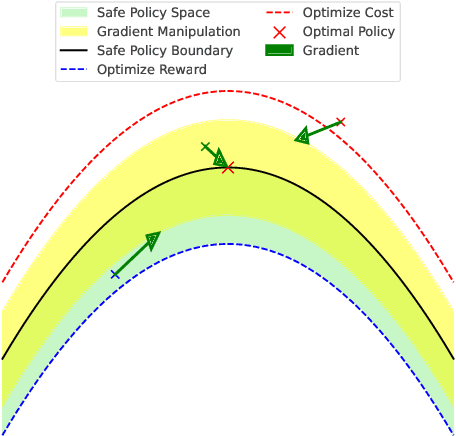
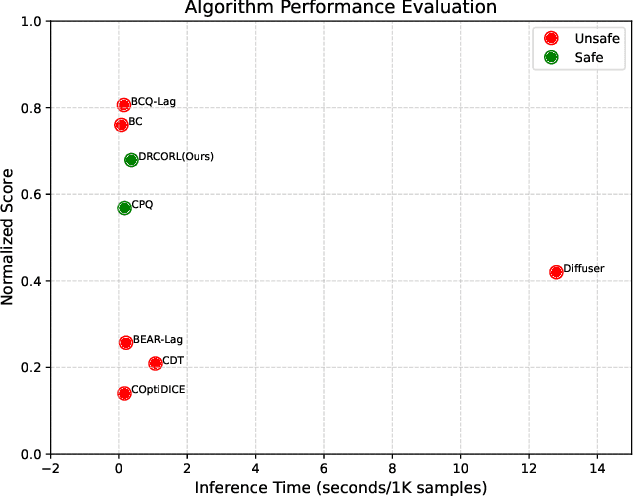
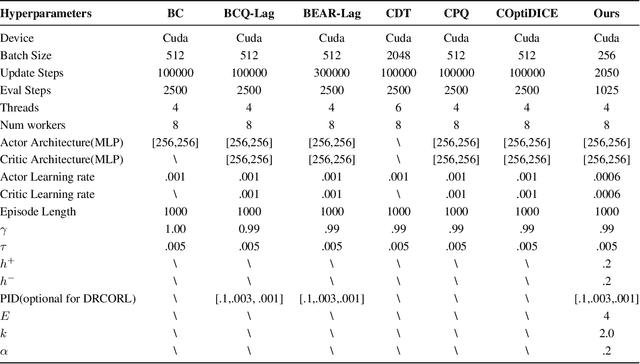
Constrained reinforcement learning (RL) seeks high-performance policies under safety constraints. We focus on an offline setting where the agent has only a fixed dataset -- common in realistic tasks to prevent unsafe exploration. To address this, we propose Diffusion-Regularized Constrained Offline Reinforcement Learning (DRCORL), which first uses a diffusion model to capture the behavioral policy from offline data and then extracts a simplified policy to enable efficient inference. We further apply gradient manipulation for safety adaptation, balancing the reward objective and constraint satisfaction. This approach leverages high-quality offline data while incorporating safety requirements. Empirical results show that DRCORL achieves reliable safety performance, fast inference, and strong reward outcomes across robot learning tasks. Compared to existing safe offline RL methods, it consistently meets cost limits and performs well with the same hyperparameters, indicating practical applicability in real-world scenarios.

Exact Recovery Guarantees for Parameterized Non-linear System Identification Problem under Adversarial Attacks

In this work, we study the system identification problem for parameterized non-linear systems using basis functions under adversarial attacks. Motivated by the LASSO-type estimators, we analyze the exact recovery property of a non-smooth estimator, which is generated by solving an embedded $\ell_1$-loss minimization problem. First, we derive necessary and sufficient conditions for the well-specifiedness of the estimator and the uniqueness of global solutions to the underlying optimization problem. Next, we provide exact recovery guarantees for the estimator under two different scenarios of boundedness and Lipschitz continuity of the basis functions. The non-asymptotic exact recovery is guaranteed with high probability, even when there are more severely corrupted data than clean data. Finally, we numerically illustrate the validity of our theory. This is the first study on the sample complexity analysis of a non-smooth estimator for the non-linear system identification problem.

A Black Swan Hypothesis in Markov Decision Process via Irrationality

Black swan events are statistically rare occurrences that carry extremely high risks. A typical view of defining black swan events is heavily assumed to originate from an unpredictable time-varying environments; however, the community lacks a comprehensive definition of black swan events. To this end, this paper challenges that the standard view is incomplete and claims that high-risk, statistically rare events can also occur in unchanging environments due to human misperception of their value and likelihood, which we call as spatial black swan event. We first carefully categorize black swan events, focusing on spatial black swan events, and mathematically formalize the definition of black swan events. We hope these definitions can pave the way for the development of algorithms to prevent such events by rationally correcting human perception

A CMDP-within-online framework for Meta-Safe Reinforcement Learning

Meta-reinforcement learning has widely been used as a learning-to-learn framework to solve unseen tasks with limited experience. However, the aspect of constraint violations has not been adequately addressed in the existing works, making their application restricted in real-world settings. In this paper, we study the problem of meta-safe reinforcement learning (Meta-SRL) through the CMDP-within-online framework to establish the first provable guarantees in this important setting. We obtain task-averaged regret bounds for the reward maximization (optimality gap) and constraint violations using gradient-based meta-learning and show that the task-averaged optimality gap and constraint satisfaction improve with task-similarity in a static environment or task-relatedness in a dynamic environment. Several technical challenges arise when making this framework practical. To this end, we propose a meta-algorithm that performs inexact online learning on the upper bounds of within-task optimality gap and constraint violations estimated by off-policy stationary distribution corrections. Furthermore, we enable the learning rates to be adapted for every task and extend our approach to settings with a competing dynamically changing oracle. Finally, experiments are conducted to demonstrate the effectiveness of our approach.

Pausing Policy Learning in Non-stationary Reinforcement Learning

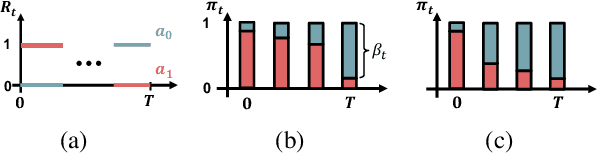
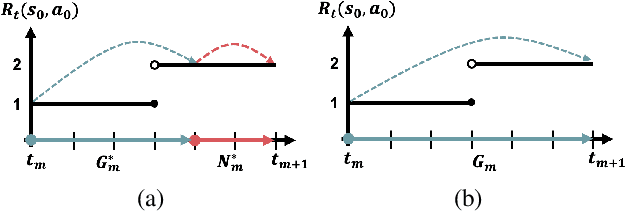
Real-time inference is a challenge of real-world reinforcement learning due to temporal differences in time-varying environments: the system collects data from the past, updates the decision model in the present, and deploys it in the future. We tackle a common belief that continually updating the decision is optimal to minimize the temporal gap. We propose forecasting an online reinforcement learning framework and show that strategically pausing decision updates yields better overall performance by effectively managing aleatoric uncertainty. Theoretically, we compute an optimal ratio between policy update and hold duration, and show that a non-zero policy hold duration provides a sharper upper bound on the dynamic regret. Our experimental evaluations on three different environments also reveal that a non-zero policy hold duration yields higher rewards compared to continuous decision updates.

Absence of spurious solutions far from ground truth: A low-rank analysis with high-order losses

Matrix sensing problems exhibit pervasive non-convexity, plaguing optimization with a proliferation of suboptimal spurious solutions. Avoiding convergence to these critical points poses a major challenge. This work provides new theoretical insights that help demystify the intricacies of the non-convex landscape. In this work, we prove that under certain conditions, critical points sufficiently distant from the ground truth matrix exhibit favorable geometry by being strict saddle points rather than troublesome local minima. Moreover, we introduce the notion of higher-order losses for the matrix sensing problem and show that the incorporation of such losses into the objective function amplifies the negative curvature around those distant critical points. This implies that increasing the complexity of the objective function via high-order losses accelerates the escape from such critical points and acts as a desirable alternative to increasing the complexity of the optimization problem via over-parametrization. By elucidating key characteristics of the non-convex optimization landscape, this work makes progress towards a comprehensive framework for tackling broader machine learning objectives plagued by non-convexity.

Algorithmic Regularization in Tensor Optimization: Towards a Lifted Approach in Matrix Sensing

Gradient descent (GD) is crucial for generalization in machine learning models, as it induces implicit regularization, promoting compact representations. In this work, we examine the role of GD in inducing implicit regularization for tensor optimization, particularly within the context of the lifted matrix sensing framework. This framework has been recently proposed to address the non-convex matrix sensing problem by transforming spurious solutions into strict saddles when optimizing over symmetric, rank-1 tensors. We show that, with sufficiently small initialization scale, GD applied to this lifted problem results in approximate rank-1 tensors and critical points with escape directions. Our findings underscore the significance of the tensor parametrization of matrix sensing, in combination with first-order methods, in achieving global optimality in such problems.

Tempo Adaption in Non-stationary Reinforcement Learning

We first raise and tackle ``time synchronization'' issue between the agent and the environment in non-stationary reinforcement learning (RL), a crucial factor hindering its real-world applications. In reality, environmental changes occur over wall-clock time ($\mathfrak{t}$) rather than episode progress ($k$), where wall-clock time signifies the actual elapsed time within the fixed duration $\mathfrak{t} \in [0, T]$. In existing works, at episode $k$, the agent rollouts a trajectory and trains a policy before transitioning to episode $k+1$. In the context of the time-desynchronized environment, however, the agent at time $\mathfrak{t}_k$ allocates $\Delta \mathfrak{t}$ for trajectory generation and training, subsequently moves to the next episode at $\mathfrak{t}_{k+1}=\mathfrak{t}_{k}+\Delta \mathfrak{t}$. Despite a fixed total episode ($K$), the agent accumulates different trajectories influenced by the choice of \textit{interaction times} ($\mathfrak{t}_1,\mathfrak{t}_2,...,\mathfrak{t}_K$), significantly impacting the sub-optimality gap of policy. We propose a Proactively Synchronizing Tempo (ProST) framework that computes optimal $\{ \mathfrak{t}_1,\mathfrak{t}_2,...,\mathfrak{t}_K \} (= \{ \mathfrak{t} \}_{1:K})$. Our main contribution is that we show optimal $\{ \mathfrak{t} \}_{1:K}$ trades-off between the policy training time (agent tempo) and how fast the environment changes (environment tempo). Theoretically, this work establishes an optimal $\{ \mathfrak{t} \}_{1:K}$ as a function of the degree of the environment's non-stationarity while also achieving a sublinear dynamic regret. Our experimental evaluation on various high dimensional non-stationary environments shows that the ProST framework achieves a higher online return at optimal $\{ \mathfrak{t} \}_{1:K}$ than the existing methods.