Finding Optimal Policy for Queueing Models: New Parameterization

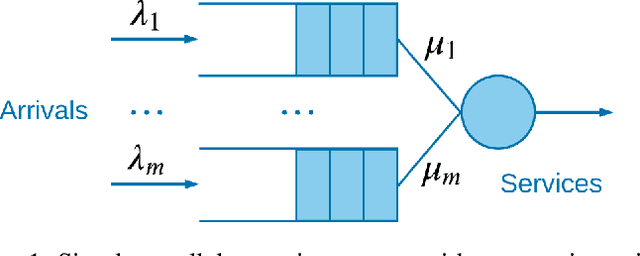
Queueing systems appear in many important real-life applications including communication networks, transportation and manufacturing systems. Reinforcement learning (RL) framework is a suitable model for the queueing control problem where the underlying dynamics are usually unknown and the agent receives little information from the environment to navigate. In this work, we investigate the optimization aspects of the queueing model as a RL environment and provide insight to learn the optimal policy efficiently. We propose a new parameterization of the policy by using the intrinsic properties of queueing network systems. Experiments show good performance of our methods with various load conditions from light to heavy traffic.

Nesterov Accelerated Shuffling Gradient Method for Convex Optimization

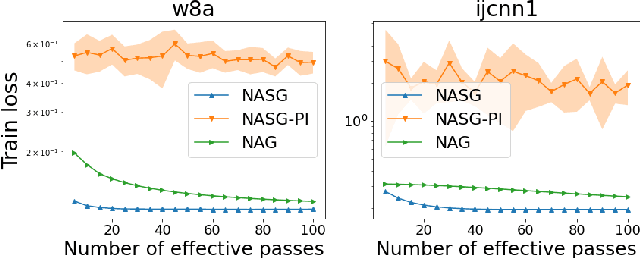
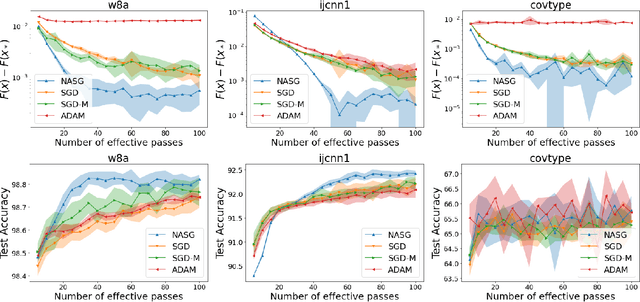
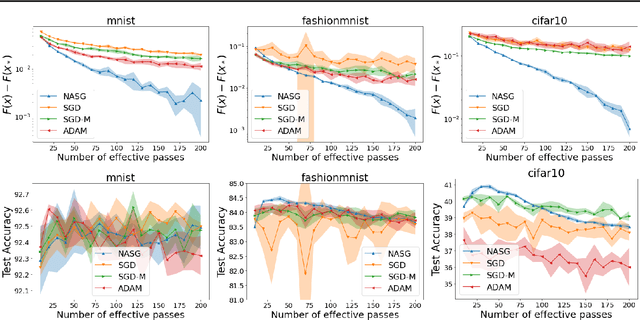
In this paper, we propose Nesterov Accelerated Shuffling Gradient (NASG), a new algorithm for the convex finite-sum minimization problems. Our method integrates the traditional Nesterov's acceleration momentum with different shuffling sampling schemes. We show that our algorithm has an improved rate of $\mathcal{O}(1/T)$ using unified shuffling schemes, where $T$ is the number of epochs. This rate is better than that of any other shuffling gradient methods in convex regime. Our convergence analysis does not require an assumption on bounded domain or a bounded gradient condition. For randomized shuffling schemes, we improve the convergence bound further. When employing some initial condition, we show that our method converges faster near the small neighborhood of the solution. Numerical simulations demonstrate the efficiency of our algorithm.

Adaptive Stochastic Optimization

Optimization lies at the heart of machine learning and signal processing. Contemporary approaches based on the stochastic gradient method are non-adaptive in the sense that their implementation employs prescribed parameter values that need to be tuned for each application. This article summarizes recent research and motivates future work on adaptive stochastic optimization methods, which have the potential to offer significant computational savings when training large-scale systems.

A Novel Smoothed Loss and Penalty Function for Noncrossing Composite Quantile Estimation via Deep Neural Networks

Uncertainty analysis in the form of probabilistic forecasting can significantly improve decision making processes in the smart power grid when integrating renewable energy sources such as wind. Whereas point forecasting provides a single expected value, probabilistic forecasts provide more information in the form of quantiles, prediction intervals, or full predictive densities. Traditionally quantile regression is applied for such forecasting and recently quantile regression neural networks have become popular for weather and renewable energy forecasting. However, one major shortcoming of composite quantile estimation in neural networks is the quantile crossover problem. This paper analyzes the effectiveness of a novel smoothed loss and penalty function for neural network architectures to prevent the quantile crossover problem. Its efficacy is examined on the wind power forecasting problem. A numerical case study is conducted using publicly available wind data from the Global Energy Forecasting Competition 2014. Multiple quantiles are estimated to form 10\%, to 90\% prediction intervals which are evaluated using a quantile score and reliability measures. Benchmark models such as the persistence and climatology distributions, multiple quantile regression, and support vector quantile regression are used for comparison where results demonstrate the proposed approach leads to improved performance while preventing the problem of overlapping quantile estimates.

Feature Engineering and Forecasting via Integration of Derivative-free Optimization and Ensemble of Sequence-to-sequence Networks: Renewable Energy Case Studies

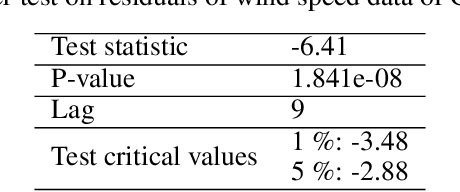
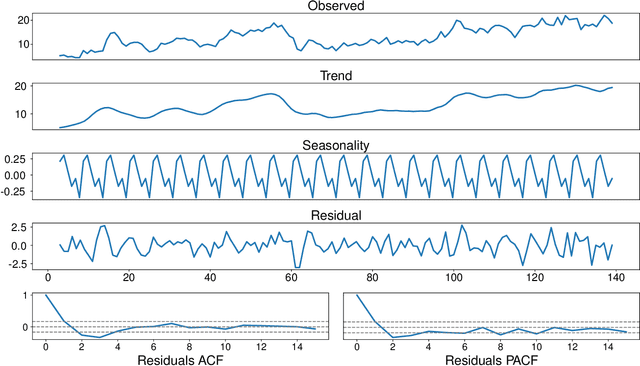
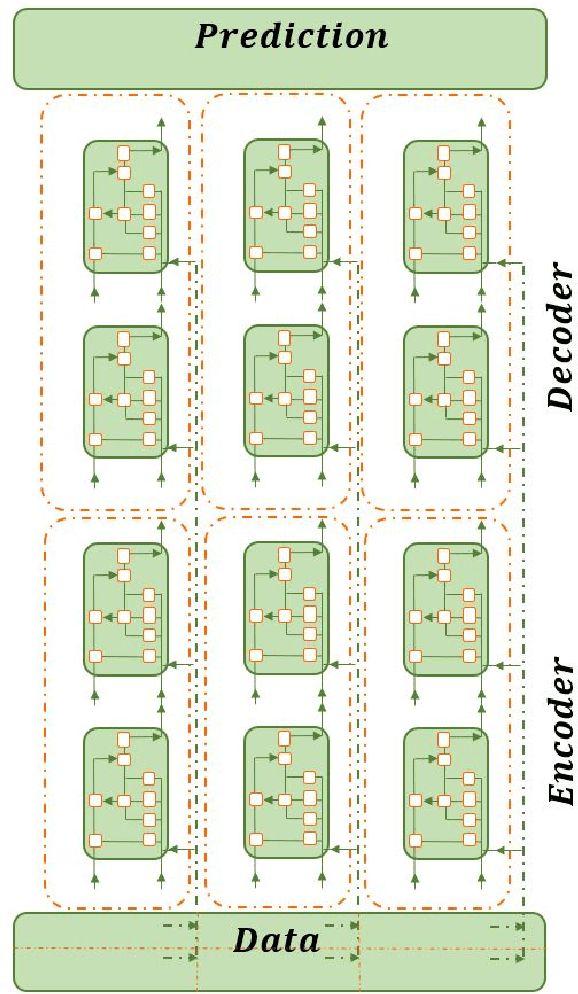
This research introduces a framework for forecasting, reconstruction and feature engineering of multivariate processes. We integrate derivative-free optimization with ensemble of sequence-to-sequence networks. We design a new resampling technique called additive which along with Bootstrap aggregating (bagging) resampling are applied to initialize the ensemble structure. We explore the proposed framework performance on three renewable energy sources wind, solar and ocean wave. We conduct several short- to long-term forecasts showing the superiority of the proposed method compare to numerous machine learning techniques. The findings indicate that the introduced method performs reasonably better when the forecasting horizon becomes longer. In addition, we modify the framework for automated feature selection. The model represents a clear interpretation of the selected features. We investigate the effects of different environmental and marine factors on the wind speed and ocean output power respectively and report the selected features. Moreover, we explore the online forecasting setting and illustrate that the model exceeds alternatives through different measurement errors.

Linear interpolation gives better gradients than Gaussian smoothing in derivative-free optimization

In this paper, we consider derivative free optimization problems, where the objective function is smooth but is computed with some amount of noise, the function evaluations are expensive and no derivative information is available. We are motivated by policy optimization problems in reinforcement learning that have recently become popular [Choromaski et al. 2018; Fazel et al. 2018; Salimans et al. 2016], and that can be formulated as derivative free optimization problems with the aforementioned characteristics. In each of these works some approximation of the gradient is constructed and a (stochastic) gradient method is applied. In [Salimans et al. 2016] the gradient information is aggregated along Gaussian directions, while in [Choromaski et al. 2018] it is computed along orthogonal direction. We provide a convergence rate analysis for a first-order line search method, similar to the ones used in the literature, and derive the conditions on the gradient approximations that ensure this convergence. We then demonstrate via rigorous analysis of the variance and by numerical comparisons on reinforcement learning tasks that the Gaussian sampling method used in [Salimans et al. 2016] is significantly inferior to the orthogonal sampling used in [Choromaski et al. 2018] as well as more general interpolation methods.

Novel and Efficient Approximations for Zero-One Loss of Linear Classifiers

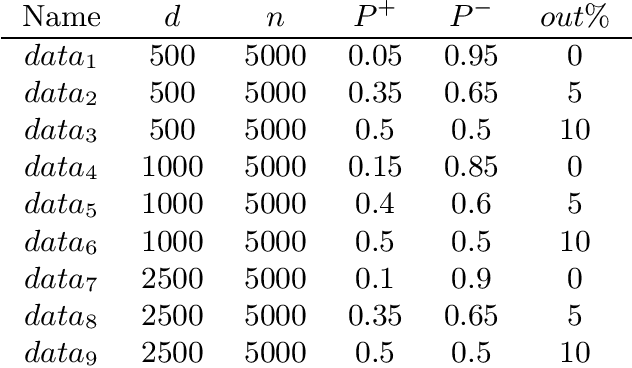
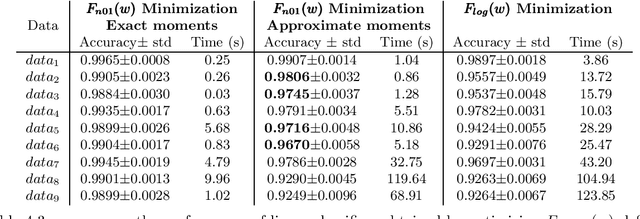
The predictive quality of machine learning models is typically measured in terms of their (approximate) expected prediction accuracy or the so-called Area Under the Curve (AUC). Minimizing the reciprocals of these measures are the goals of supervised learning. However, when the models are constructed by the means of empirical risk minimization (ERM), surrogate functions such as the logistic loss or hinge loss are optimized instead. In this work, we show that in the case of linear predictors, the expected error and the expected ranking loss can be effectively approximated by smooth functions whose closed form expressions and those of their first (and second) order derivatives depend on the first and second moments of the data distribution, which can be precomputed. Hence, the complexity of an optimization algorithm applied to these functions does not depend on the size of the training data. These approximation functions are derived under the assumption that the output of the linear classifier for a given data set has an approximately normal distribution. We argue that this assumption is significantly weaker than the Gaussian assumption on the data itself and we support this claim by demonstrating that our new approximation is quite accurate on data sets that are not necessarily Gaussian. We present computational results that show that our proposed approximations and related optimization algorithms can produce linear classifiers with similar or better test accuracy or AUC, than those obtained using state-of-the-art approaches, in a fraction of the time.

Inexact SARAH Algorithm for Stochastic Optimization

We develop and analyze a variant of variance reducing stochastic gradient algorithm, known as SARAH, which does not require computation of the exact gradient. Thus this new method can be applied to general expectation minimization problems rather than only finite sum problems. While the original SARAH algorithm, as well as its predecessor, SVRG, require an exact gradient computation on each outer iteration, the inexact variant of SARAH (iSARAH), which we develop here, requires only stochastic gradient computed on a mini-batch of sufficient size. The proposed method combines variance reduction via sample size selection and iterative stochastic gradient updates. We analyze the convergence rate of the algorithms for strongly convex, convex, and nonconvex cases with appropriate mini-batch size selected for each case. We show that with an additional, reasonable, assumption iSARAH achieves the best known complexity among stochastic methods in the case of general convex case stochastic value functions.

New Convergence Aspects of Stochastic Gradient Algorithms

The classical convergence analysis of SGD is carried out under the assumption that the norm of the stochastic gradient is uniformly bounded. While this might hold for some loss functions, it is violated for cases where the objective function is strongly convex. In Bottou et al. (2016), a new analysis of convergence of SGD is performed under the assumption that stochastic gradients are bounded with respect to the true gradient norm. We show that for stochastic problems arising in machine learning such bound always holds; and we also propose an alternative convergence analysis of SGD with diminishing learning rate regime, which results in more relaxed conditions than those in Bottou et al. (2016). We then move on the asynchronous parallel setting, and prove convergence of Hogwild! algorithm in the same regime in the case of diminished learning rate. It is well-known that SGD converges if a sequence of learning rates $\{\eta_t\}$ satisfies $\sum_{t=0}^\infty \eta_t \rightarrow \infty$ and $\sum_{t=0}^\infty \eta^2_t < \infty$. We show the convergence of SGD for strongly convex objective function without using bounded gradient assumption when $\{\eta_t\}$ is a diminishing sequence and $\sum_{t=0}^\infty \eta_t \rightarrow \infty$. In other words, we extend the current state-of-the-art class of learning rates satisfying the convergence of SGD.

A Stochastic Trust Region Algorithm Based on Careful Step Normalization

An algorithm is proposed for solving stochastic and finite sum minimization problems. Based on a trust region methodology, the algorithm employs normalized steps, at least as long as the norms of the stochastic gradient estimates are within a specified interval. The complete algorithm---which dynamically chooses whether or not to employ normalized steps---is proved to have convergence guarantees that are similar to those possessed by a traditional stochastic gradient approach under various sets of conditions related to the accuracy of the stochastic gradient estimates and choice of stepsize sequence. The results of numerical experiments are presented when the method is employed to minimize convex and nonconvex machine learning test problems. These results illustrate that the method can outperform a traditional stochastic gradient approach.