Shuffling Gradient-Based Methods for Nonconvex-Concave Minimax Optimization

This paper aims at developing novel shuffling gradient-based methods for tackling two classes of minimax problems: nonconvex-linear and nonconvex-strongly concave settings. The first algorithm addresses the nonconvex-linear minimax model and achieves the state-of-the-art oracle complexity typically observed in nonconvex optimization. It also employs a new shuffling estimator for the "hyper-gradient", departing from standard shuffling techniques in optimization. The second method consists of two variants: semi-shuffling and full-shuffling schemes. These variants tackle the nonconvex-strongly concave minimax setting. We establish their oracle complexity bounds under standard assumptions, which, to our best knowledge, are the best-known for this specific setting. Numerical examples demonstrate the performance of our algorithms and compare them with two other methods. Our results show that the new methods achieve comparable performance with SGD, supporting the potential of incorporating shuffling strategies into minimax algorithms.

Shuffling Momentum Gradient Algorithm for Convex Optimization

The Stochastic Gradient Descent method (SGD) and its stochastic variants have become methods of choice for solving finite-sum optimization problems arising from machine learning and data science thanks to their ability to handle large-scale applications and big datasets. In the last decades, researchers have made substantial effort to study the theoretical performance of SGD and its shuffling variants. However, only limited work has investigated its shuffling momentum variants, including shuffling heavy-ball momentum schemes for non-convex problems and Nesterov's momentum for convex settings. In this work, we extend the analysis of the shuffling momentum gradient method developed in [Tran et al (2021)] to both finite-sum convex and strongly convex optimization problems. We provide the first analysis of shuffling momentum-based methods for the strongly convex setting, attaining a convergence rate of $O(1/nT^2)$, where $n$ is the number of samples and $T$ is the number of training epochs. Our analysis is a state-of-the-art, matching the best rates of existing shuffling stochastic gradient algorithms in the literature.

A Supervised Contrastive Learning Pretrain-Finetune Approach for Time Series

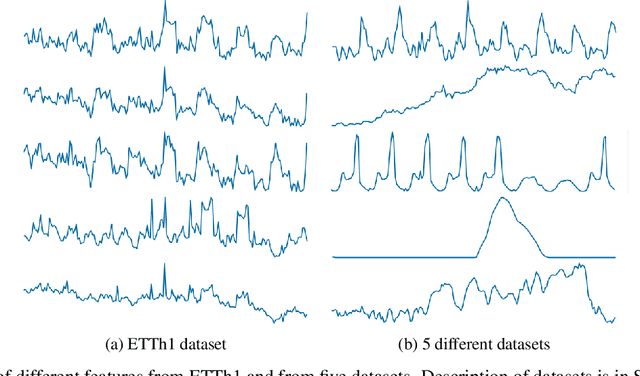
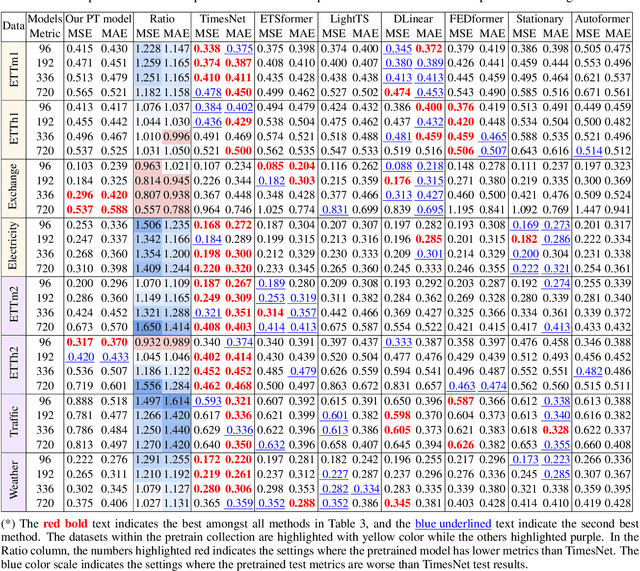
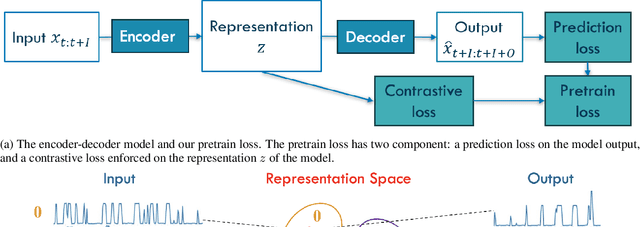
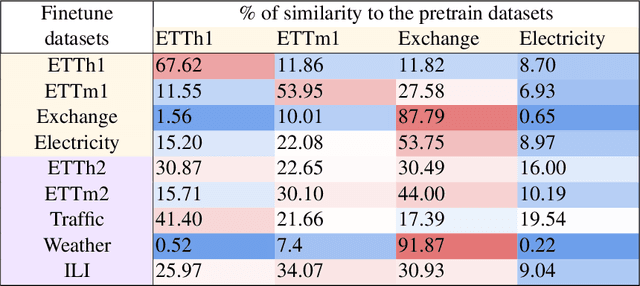
Foundation models have recently gained attention within the field of machine learning thanks to its efficiency in broad data processing. While researchers had attempted to extend this success to time series models, the main challenge is effectively extracting representations and transferring knowledge from pretraining datasets to the target finetuning dataset. To tackle this issue, we introduce a novel pretraining procedure that leverages supervised contrastive learning to distinguish features within each pretraining dataset. This pretraining phase enables a probabilistic similarity metric, which assesses the likelihood of a univariate sample being closely related to one of the pretraining datasets. Subsequently, using this similarity metric as a guide, we propose a fine-tuning procedure designed to enhance the accurate prediction of the target data by aligning it more closely with the learned dynamics of the pretraining datasets. Our experiments have shown promising results which demonstrate the efficacy of our approach.

Learning Robust and Consistent Time Series Representations: A Dilated Inception-Based Approach

Representation learning for time series has been an important research area for decades. Since the emergence of the foundation models, this topic has attracted a lot of attention in contrastive self-supervised learning, to solve a wide range of downstream tasks. However, there have been several challenges for contrastive time series processing. First, there is no work considering noise, which is one of the critical factors affecting the efficacy of time series tasks. Second, there is a lack of efficient yet lightweight encoder architectures that can learn informative representations robust to various downstream tasks. To fill in these gaps, we initiate a novel sampling strategy that promotes consistent representation learning with the presence of noise in natural time series. In addition, we propose an encoder architecture that utilizes dilated convolution within the Inception block to create a scalable and robust network architecture with a wide receptive field. Experiments demonstrate that our method consistently outperforms state-of-the-art methods in forecasting, classification, and abnormality detection tasks, e.g. ranks first over two-thirds of the classification UCR datasets, with only $40\%$ of the parameters compared to the second-best approach. Our source code for CoInception framework is accessible at https://github.com/anhduy0911/CoInception.

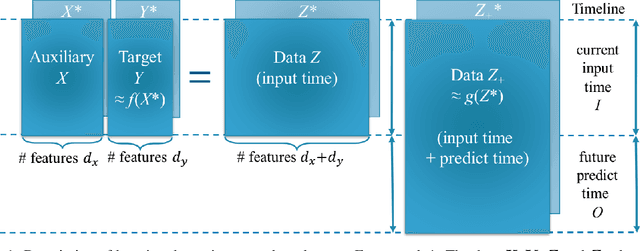
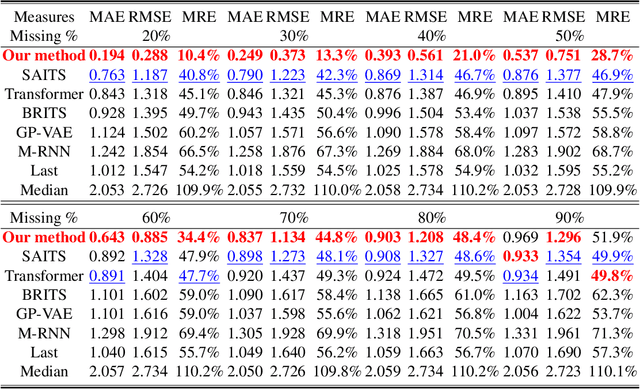
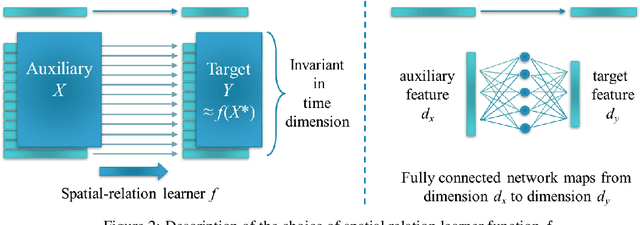
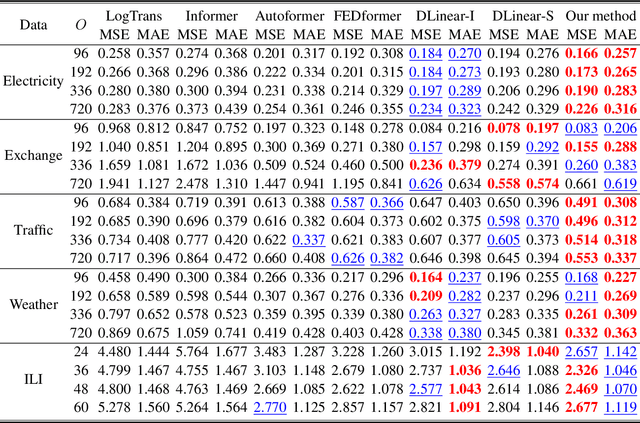
An End-to-End Time Series Model for Simultaneous Imputation and Forecast

Time series forecasting using historical data has been an interesting and challenging topic, especially when the data is corrupted by missing values. In many industrial problem, it is important to learn the inference function between the auxiliary observations and target variables as it provides additional knowledge when the data is not fully observed. We develop an end-to-end time series model that aims to learn the such inference relation and make a multiple-step ahead forecast. Our framework trains jointly two neural networks, one to learn the feature-wise correlations and the other for the modeling of temporal behaviors. Our model is capable of simultaneously imputing the missing entries and making a multiple-step ahead prediction. The experiments show good overall performance of our framework over existing methods in both imputation and forecasting tasks.

Finding Optimal Policy for Queueing Models: New Parameterization

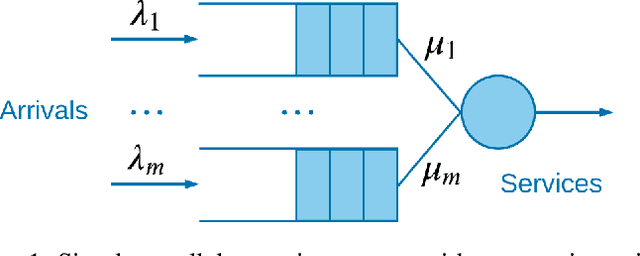
Queueing systems appear in many important real-life applications including communication networks, transportation and manufacturing systems. Reinforcement learning (RL) framework is a suitable model for the queueing control problem where the underlying dynamics are usually unknown and the agent receives little information from the environment to navigate. In this work, we investigate the optimization aspects of the queueing model as a RL environment and provide insight to learn the optimal policy efficiently. We propose a new parameterization of the policy by using the intrinsic properties of queueing network systems. Experiments show good performance of our methods with various load conditions from light to heavy traffic.

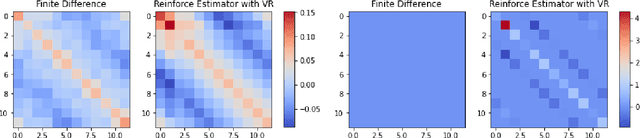
On the Convergence to a Global Solution of Shuffling-Type Gradient Algorithms

Stochastic gradient descent (SGD) algorithm is the method of choice in many machine learning tasks thanks to its scalability and efficiency in dealing with large-scale problems. In this paper, we focus on the shuffling version of SGD which matches the mainstream practical heuristics. We show the convergence to a global solution of shuffling SGD for a class of non-convex functions under over-parameterized settings. Our analysis employs more relaxed non-convex assumptions than previous literature. Nevertheless, we maintain the desired computational complexity as shuffling SGD has achieved in the general convex setting.

Nesterov Accelerated Shuffling Gradient Method for Convex Optimization

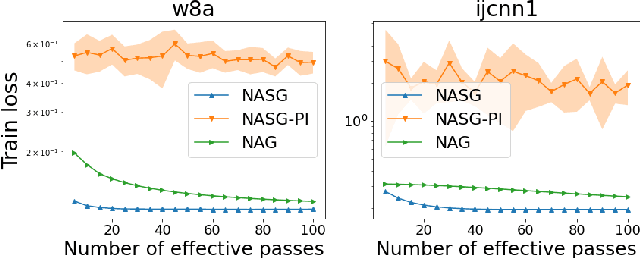
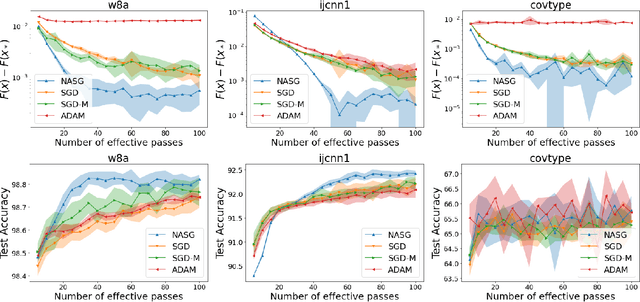
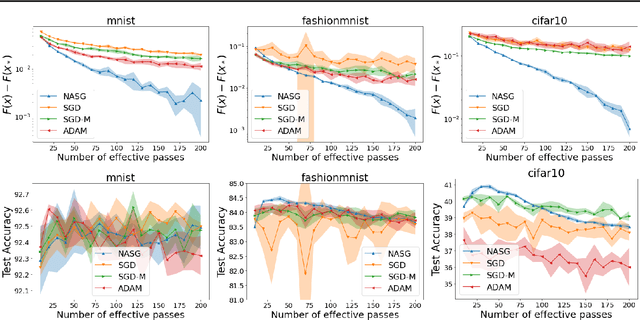
In this paper, we propose Nesterov Accelerated Shuffling Gradient (NASG), a new algorithm for the convex finite-sum minimization problems. Our method integrates the traditional Nesterov's acceleration momentum with different shuffling sampling schemes. We show that our algorithm has an improved rate of $\mathcal{O}(1/T)$ using unified shuffling schemes, where $T$ is the number of epochs. This rate is better than that of any other shuffling gradient methods in convex regime. Our convergence analysis does not require an assumption on bounded domain or a bounded gradient condition. For randomized shuffling schemes, we improve the convergence bound further. When employing some initial condition, we show that our method converges faster near the small neighborhood of the solution. Numerical simulations demonstrate the efficiency of our algorithm.

Finite-Sum Optimization: A New Perspective for Convergence to a Global Solution

Deep neural networks (DNNs) have shown great success in many machine learning tasks. Their training is challenging since the loss surface of the network architecture is generally non-convex, or even non-smooth. How and under what assumptions is guaranteed convergence to a \textit{global} minimum possible? We propose a reformulation of the minimization problem allowing for a new recursive algorithmic framework. By using bounded style assumptions, we prove convergence to an $\varepsilon$-(global) minimum using $\mathcal{\tilde{O}}(1/\varepsilon^3)$ gradient computations. Our theoretical foundation motivates further study, implementation, and optimization of the new algorithmic framework and further investigation of its non-standard bounded style assumptions. This new direction broadens our understanding of why and under what circumstances training of a DNN converges to a global minimum.

Shuffling Gradient-Based Methods with Momentum

We combine two advanced ideas widely used in optimization for machine learning: shuffling strategy and momentum technique to develop a novel shuffling gradient-based method with momentum to approximate a stationary point of non-convex finite-sum minimization problems. While our method is inspired by momentum techniques, its update is significantly different from existing momentum-based methods. We establish that our algorithm achieves a state-of-the-art convergence rate for both constant and diminishing learning rates under standard assumptions (i.e., $L$-smoothness and bounded variance). When the shuffling strategy is fixed, we develop another new algorithm that is similar to existing momentum methods. This algorithm covers the single-shuffling and incremental gradient schemes as special cases. We prove the same convergence rate of this algorithm under the $L$-smoothness and bounded gradient assumptions. We demonstrate our algorithms via numerical simulations on standard datasets and compare them with existing shuffling methods. Our tests have shown encouraging performance of the new algorithms.