Nesterov Accelerated Shuffling Gradient Method for Convex Optimization
Paper and Code
Feb 07, 2022
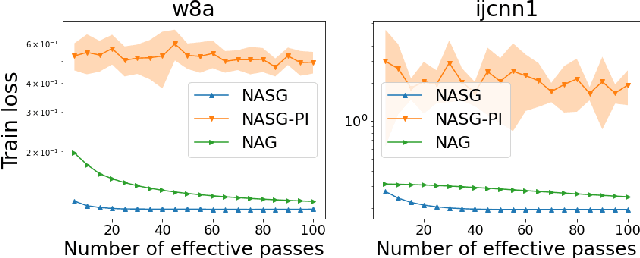
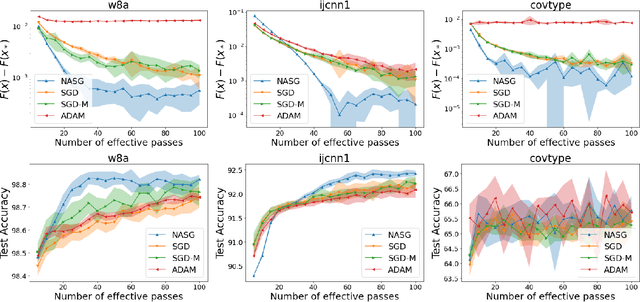
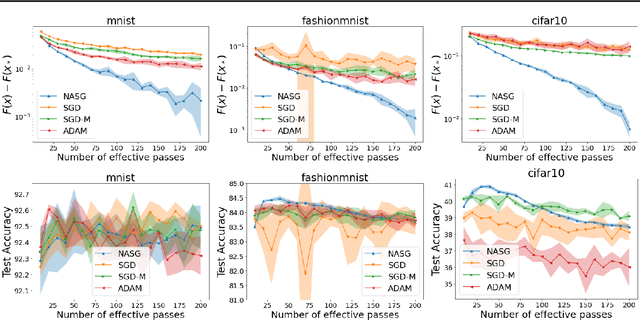
In this paper, we propose Nesterov Accelerated Shuffling Gradient (NASG), a new algorithm for the convex finite-sum minimization problems. Our method integrates the traditional Nesterov's acceleration momentum with different shuffling sampling schemes. We show that our algorithm has an improved rate of $\mathcal{O}(1/T)$ using unified shuffling schemes, where $T$ is the number of epochs. This rate is better than that of any other shuffling gradient methods in convex regime. Our convergence analysis does not require an assumption on bounded domain or a bounded gradient condition. For randomized shuffling schemes, we improve the convergence bound further. When employing some initial condition, we show that our method converges faster near the small neighborhood of the solution. Numerical simulations demonstrate the efficiency of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge