Quantifying and Mitigating Privacy Risks for Tabular Generative Models

Synthetic data from generative models emerges as the privacy-preserving data-sharing solution. Such a synthetic data set shall resemble the original data without revealing identifiable private information. The backbone technology of tabular synthesizers is rooted in image generative models, ranging from Generative Adversarial Networks (GANs) to recent diffusion models. Recent prior work sheds light on the utility-privacy tradeoff on tabular data, revealing and quantifying privacy risks on synthetic data. We first conduct an exhaustive empirical analysis, highlighting the utility-privacy tradeoff of five state-of-the-art tabular synthesizers, against eight privacy attacks, with a special focus on membership inference attacks. Motivated by the observation of high data quality but also high privacy risk in tabular diffusion, we propose DP-TLDM, Differentially Private Tabular Latent Diffusion Model, which is composed of an autoencoder network to encode the tabular data and a latent diffusion model to synthesize the latent tables. Following the emerging f-DP framework, we apply DP-SGD to train the auto-encoder in combination with batch clipping and use the separation value as the privacy metric to better capture the privacy gain from DP algorithms. Our empirical evaluation demonstrates that DP-TLDM is capable of achieving a meaningful theoretical privacy guarantee while also significantly enhancing the utility of synthetic data. Specifically, compared to other DP-protected tabular generative models, DP-TLDM improves the synthetic quality by an average of 35% in data resemblance, 15% in the utility for downstream tasks, and 50% in data discriminability, all while preserving a comparable level of privacy risk.

Considerations on the Theory of Training Models with Differential Privacy

In federated learning collaborative learning takes place by a set of clients who each want to remain in control of how their local training data is used, in particular, how can each client's local training data remain private? Differential privacy is one method to limit privacy leakage. We provide a general overview of its framework and provable properties, adopt the more recent hypothesis based definition called Gaussian DP or $f$-DP, and discuss Differentially Private Stochastic Gradient Descent (DP-SGD). We stay at a meta level and attempt intuitive explanations and insights \textit{in this book chapter}.

Gradient Descent-Type Methods: Background and Simple Unified Convergence Analysis

In this book chapter, we briefly describe the main components that constitute the gradient descent method and its accelerated and stochastic variants. We aim at explaining these components from a mathematical point of view, including theoretical and practical aspects, but at an elementary level. We will focus on basic variants of the gradient descent method and then extend our view to recent variants, especially variance-reduced stochastic gradient schemes (SGD). Our approach relies on revealing the structures presented inside the problem and the assumptions imposed on the objective function. Our convergence analysis unifies several known results and relies on a general, but elementary recursive expression. We have illustrated this analysis on several common schemes.

Generalizing DP-SGD with Shuffling and Batching Clipping

Classical differential private DP-SGD implements individual clipping with random subsampling, which forces a mini-batch SGD approach. We provide a general differential private algorithmic framework that goes beyond DP-SGD and allows any possible first order optimizers (e.g., classical SGD and momentum based SGD approaches) in combination with batch clipping, which clips an aggregate of computed gradients rather than summing clipped gradients (as is done in individual clipping). The framework also admits sampling techniques beyond random subsampling such as shuffling. Our DP analysis follows the $f$-DP approach and introduces a new proof technique which allows us to also analyse group privacy. In particular, for $E$ epochs work and groups of size $g$, we show a $\sqrt{g E}$ DP dependency for batch clipping with shuffling. This is much better than the previously anticipated linear dependency in $g$ and is much better than the previously expected square root dependency on the total number of rounds within $E$ epochs which is generally much more than $\sqrt{E}$.

Game Theoretic Mixed Experts for Combinational Adversarial Machine Learning

Recent advances in adversarial machine learning have shown that defenses considered to be robust are actually susceptible to adversarial attacks which are specifically tailored to target their weaknesses. These defenses include Barrage of Random Transforms (BaRT), Friendly Adversarial Training (FAT), Trash is Treasure (TiT) and ensemble models made up of Vision Transformers (ViTs), Big Transfer models and Spiking Neural Networks (SNNs). A natural question arises: how can one best leverage a combination of adversarial defenses to thwart such attacks? In this paper, we provide a game-theoretic framework for ensemble adversarial attacks and defenses which answers this question. In addition to our framework we produce the first adversarial defense transferability study to further motivate a need for combinational defenses utilizing a diverse set of defense architectures. Our framework is called Game theoretic Mixed Experts (GaME) and is designed to find the Mixed-Nash strategy for a defender when facing an attacker employing compositional adversarial attacks. We show that this framework creates an ensemble of defenses with greater robustness than multiple state-of-the-art, single-model defenses in addition to combinational defenses with uniform probability distributions. Overall, our framework and analyses advance the field of adversarial machine learning by yielding new insights into compositional attack and defense formulations.

Finite-Sum Optimization: A New Perspective for Convergence to a Global Solution

Deep neural networks (DNNs) have shown great success in many machine learning tasks. Their training is challenging since the loss surface of the network architecture is generally non-convex, or even non-smooth. How and under what assumptions is guaranteed convergence to a \textit{global} minimum possible? We propose a reformulation of the minimization problem allowing for a new recursive algorithmic framework. By using bounded style assumptions, we prove convergence to an $\varepsilon$-(global) minimum using $\mathcal{\tilde{O}}(1/\varepsilon^3)$ gradient computations. Our theoretical foundation motivates further study, implementation, and optimization of the new algorithmic framework and further investigation of its non-standard bounded style assumptions. This new direction broadens our understanding of why and under what circumstances training of a DNN converges to a global minimum.

Back in Black: A Comparative Evaluation of Recent State-Of-The-Art Black-Box Attacks

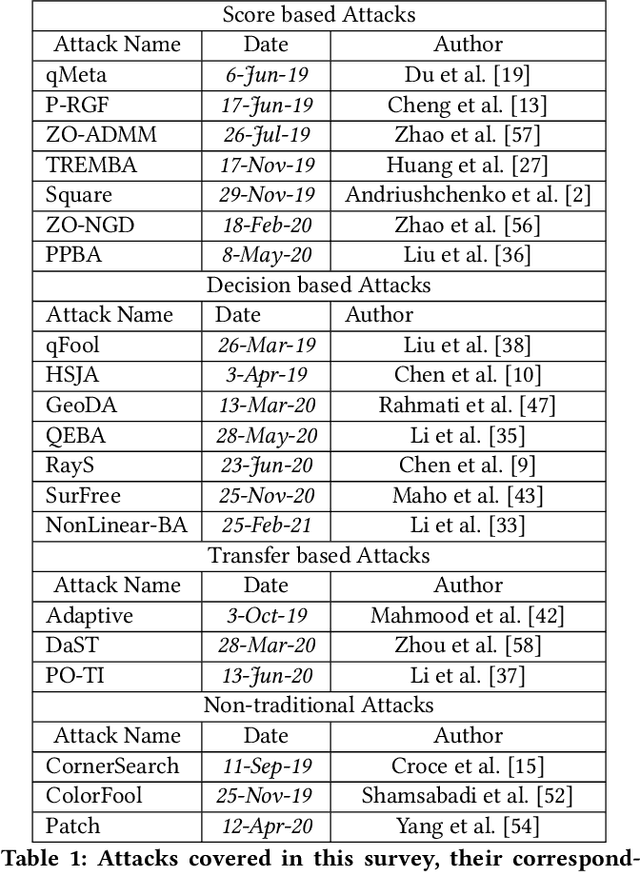
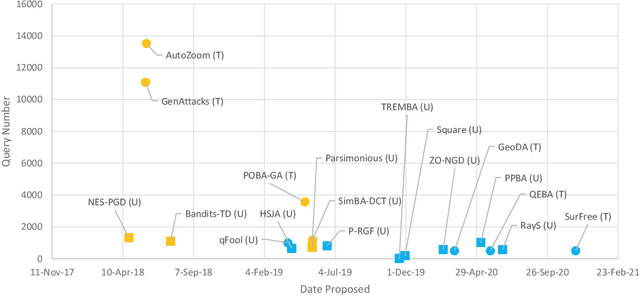
The field of adversarial machine learning has experienced a near exponential growth in the amount of papers being produced since 2018. This massive information output has yet to be properly processed and categorized. In this paper, we seek to help alleviate this problem by systematizing the recent advances in adversarial machine learning black-box attacks since 2019. Our survey summarizes and categorizes 20 recent black-box attacks. We also present a new analysis for understanding the attack success rate with respect to the adversarial model used in each paper. Overall, our paper surveys a wide body of literature to highlight recent attack developments and organizes them into four attack categories: score based attacks, decision based attacks, transfer attacks and non-traditional attacks. Further, we provide a new mathematical framework to show exactly how attack results can fairly be compared.

On the Robustness of Vision Transformers to Adversarial Examples

Recent advances in attention-based networks have shown that Vision Transformers can achieve state-of-the-art or near state-of-the-art results on many image classification tasks. This puts transformers in the unique position of being a promising alternative to traditional convolutional neural networks (CNNs). While CNNs have been carefully studied with respect to adversarial attacks, the same cannot be said of Vision Transformers. In this paper, we study the robustness of Vision Transformers to adversarial examples. Our analyses of transformer security is divided into three parts. First, we test the transformer under standard white-box and black-box attacks. Second, we study the transferability of adversarial examples between CNNs and transformers. We show that adversarial examples do not readily transfer between CNNs and transformers. Based on this finding, we analyze the security of a simple ensemble defense of CNNs and transformers. By creating a new attack, the self-attention blended gradient attack, we show that such an ensemble is not secure under a white-box adversary. However, under a black-box adversary, we show that an ensemble can achieve unprecedented robustness without sacrificing clean accuracy. Our analysis for this work is done using six types of white-box attacks and two types of black-box attacks. Our study encompasses multiple Vision Transformers, Big Transfer Models and CNN architectures trained on CIFAR-10, CIFAR-100 and ImageNet.

Differential Private Hogwild! over Distributed Local Data Sets

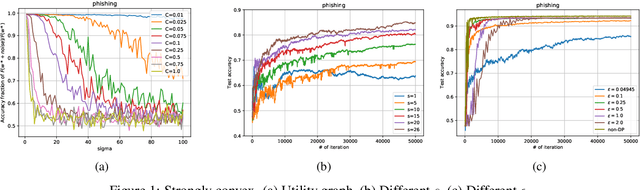
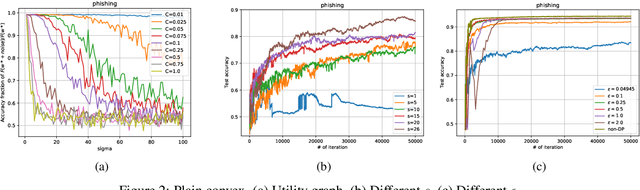
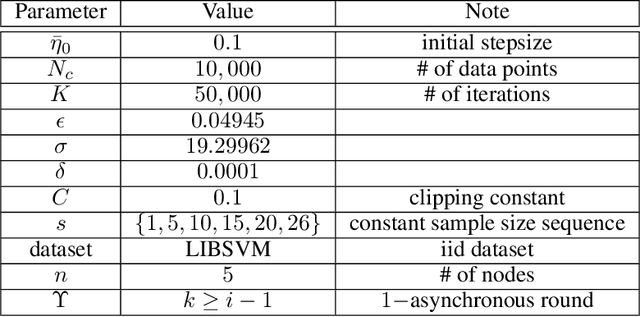
We consider the Hogwild! setting where clients use local SGD iterations with Gaussian based Differential Privacy (DP) for their own local data sets with the aim of (1) jointly converging to a global model (by interacting at a round to round basis with a centralized server that aggregates local SGD updates into a global model) while (2) keeping each local data set differentially private with respect to the outside world (this includes all other clients who can monitor client-server interactions). We show for a broad class of sample size sequences (this defines the number of local SGD iterations for each round) that a local data set is $(\epsilon,\delta)$-DP if the standard deviation $\sigma$ of the added Gaussian noise per round interaction with the centralized server is at least $\sqrt{2(\epsilon+ \ln(1/\delta))/\epsilon}$.

Hogwild! over Distributed Local Data Sets with Linearly Increasing Mini-Batch Sizes

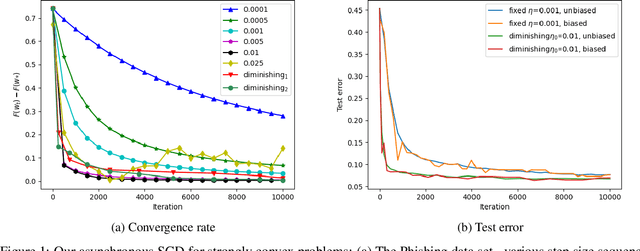
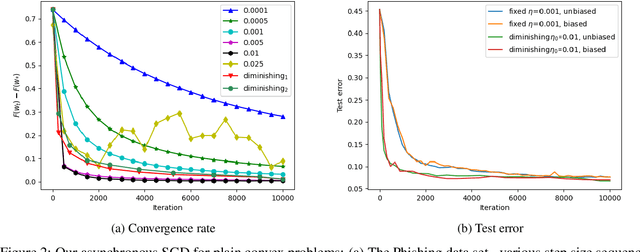
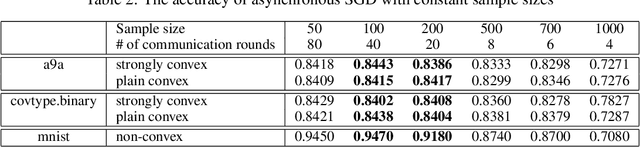
Hogwild! implements asynchronous Stochastic Gradient Descent (SGD) where multiple threads in parallel access a common repository containing training data, perform SGD iterations and update shared state that represents a jointly learned (global) model. We consider big data analysis where training data is distributed among local data sets -- and we wish to move SGD computations to local compute nodes where local data resides. The results of these local SGD computations are aggregated by a central "aggregator" which mimics Hogwild!. We show how local compute nodes can start choosing small mini-batch sizes which increase to larger ones in order to reduce communication cost (round interaction with the aggregator). We prove a tight and novel non-trivial convergence analysis for strongly convex problems which does not use the bounded gradient assumption as seen in many existing publications. The tightness is a consequence of our proofs for lower and upper bounds of the convergence rate, which show a constant factor difference. We show experimental results for plain convex and non-convex problems for biased and unbiased local data sets.