Differential Private Hogwild! over Distributed Local Data Sets

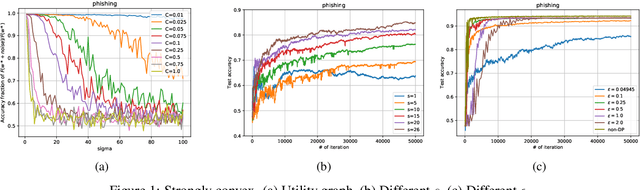
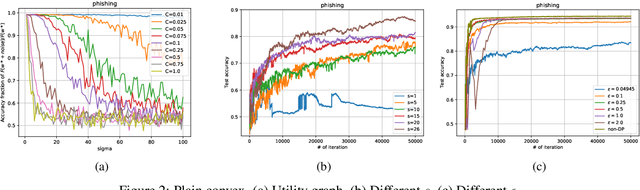
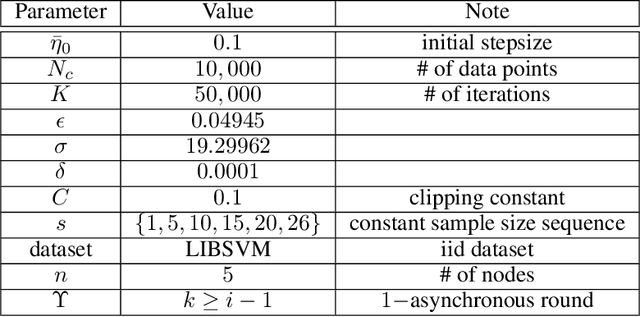
We consider the Hogwild! setting where clients use local SGD iterations with Gaussian based Differential Privacy (DP) for their own local data sets with the aim of (1) jointly converging to a global model (by interacting at a round to round basis with a centralized server that aggregates local SGD updates into a global model) while (2) keeping each local data set differentially private with respect to the outside world (this includes all other clients who can monitor client-server interactions). We show for a broad class of sample size sequences (this defines the number of local SGD iterations for each round) that a local data set is $(\epsilon,\delta)$-DP if the standard deviation $\sigma$ of the added Gaussian noise per round interaction with the centralized server is at least $\sqrt{2(\epsilon+ \ln(1/\delta))/\epsilon}$.