Distributed Learning and its Application for Time-Series Prediction

Extreme events are occurrences whose magnitude and potential cause extensive damage on people, infrastructure, and the environment. Motivated by the extreme nature of the current global health landscape, which is plagued by the coronavirus pandemic, we seek to better understand and model extreme events. Modeling extreme events is common in practice and plays an important role in time-series prediction applications. Our goal is to (i) compare and investigate the effect of some common extreme events modeling methods to explore which method can be practical in reality and (ii) accelerate the deep learning training process, which commonly uses deep recurrent neural network (RNN), by implementing the asynchronous local Stochastic Gradient Descent (SGD) framework among multiple compute nodes. In order to verify our distributed extreme events modeling, we evaluate our proposed framework on a stock data set S\&P500, with a standard recurrent neural network. Our intuition is to explore the (best) extreme events modeling method which could work well under the distributed deep learning setting. Moreover, by using asynchronous distributed learning, we aim to significantly reduce the communication cost among the compute nodes and central server, which is the main bottleneck of almost all distributed learning frameworks. We implement our proposed work and evaluate its performance on representative data sets, such as S&P500 stock in $5$-year period. The experimental results validate the correctness of the design principle and show a significant training duration reduction upto $8$x, compared to the baseline single compute node. Our results also show that our proposed work can achieve the same level of test accuracy, compared to the baseline setting.

Differential Private Hogwild! over Distributed Local Data Sets

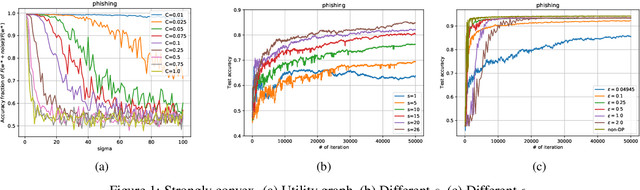
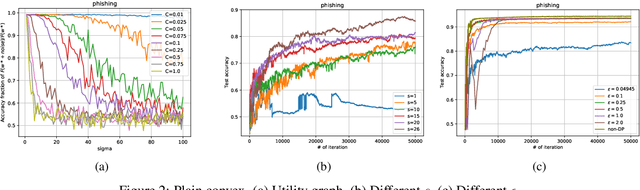
We consider the Hogwild! setting where clients use local SGD iterations with Gaussian based Differential Privacy (DP) for their own local data sets with the aim of (1) jointly converging to a global model (by interacting at a round to round basis with a centralized server that aggregates local SGD updates into a global model) while (2) keeping each local data set differentially private with respect to the outside world (this includes all other clients who can monitor client-server interactions). We show for a broad class of sample size sequences (this defines the number of local SGD iterations for each round) that a local data set is $(\epsilon,\delta)$-DP if the standard deviation $\sigma$ of the added Gaussian noise per round interaction with the centralized server is at least $\sqrt{2(\epsilon+ \ln(1/\delta))/\epsilon}$.

Hogwild! over Distributed Local Data Sets with Linearly Increasing Mini-Batch Sizes

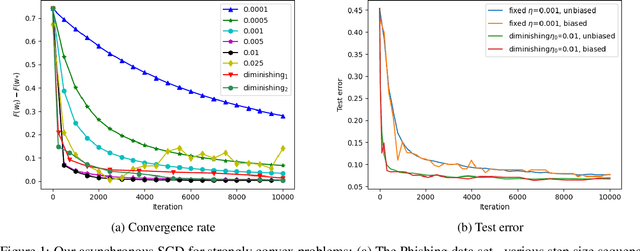
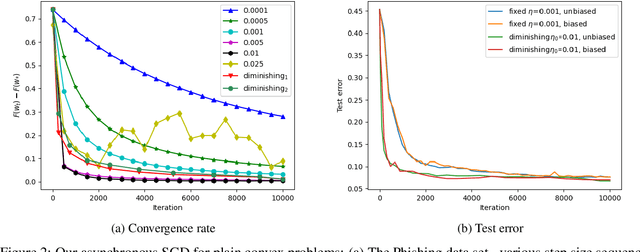
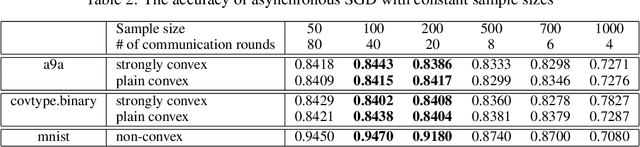
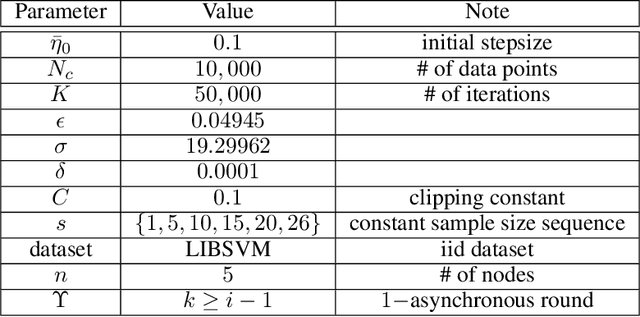
Hogwild! implements asynchronous Stochastic Gradient Descent (SGD) where multiple threads in parallel access a common repository containing training data, perform SGD iterations and update shared state that represents a jointly learned (global) model. We consider big data analysis where training data is distributed among local data sets -- and we wish to move SGD computations to local compute nodes where local data resides. The results of these local SGD computations are aggregated by a central "aggregator" which mimics Hogwild!. We show how local compute nodes can start choosing small mini-batch sizes which increase to larger ones in order to reduce communication cost (round interaction with the aggregator). We prove a tight and novel non-trivial convergence analysis for strongly convex problems which does not use the bounded gradient assumption as seen in many existing publications. The tightness is a consequence of our proofs for lower and upper bounds of the convergence rate, which show a constant factor difference. We show experimental results for plain convex and non-convex problems for biased and unbiased local data sets.

Asynchronous Federated Learning with Reduced Number of Rounds and with Differential Privacy from Less Aggregated Gaussian Noise

The feasibility of federated learning is highly constrained by the server-clients infrastructure in terms of network communication. Most newly launched smartphones and IoT devices are equipped with GPUs or sufficient computing hardware to run powerful AI models. However, in case of the original synchronous federated learning, client devices suffer waiting times and regular communication between clients and server is required. This implies more sensitivity to local model training times and irregular or missed updates, hence, less or limited scalability to large numbers of clients and convergence rates measured in real time will suffer. We propose a new algorithm for asynchronous federated learning which eliminates waiting times and reduces overall network communication - we provide rigorous theoretical analysis for strongly convex objective functions and provide simulation results. By adding Gaussian noise we show how our algorithm can be made differentially private -- new theorems show how the aggregated added Gaussian noise is significantly reduced.