Activations Through Extensions: A Framework To Boost Performance Of Neural Networks

Activation functions are non-linearities in neural networks that allow them to learn complex mapping between inputs and outputs. Typical choices for activation functions are ReLU, Tanh, Sigmoid etc., where the choice generally depends on the application domain. In this work, we propose a framework/strategy that unifies several works on activation functions and theoretically explains the performance benefits of these works. We also propose novel techniques that originate from the framework and allow us to obtain ``extensions'' (i.e. special generalizations of a given neural network) of neural networks through operations on activation functions. We theoretically and empirically show that ``extensions'' of neural networks have performance benefits compared to vanilla neural networks with insignificant space and time complexity costs on standard test functions. We also show the benefits of neural network ``extensions'' in the time-series domain on real-world datasets.

TabularFM: An Open Framework For Tabular Foundational Models

Foundational models (FMs), pretrained on extensive datasets using self-supervised techniques, are capable of learning generalized patterns from large amounts of data. This reduces the need for extensive labeled datasets for each new task, saving both time and resources by leveraging the broad knowledge base established during pretraining. Most research on FMs has primarily focused on unstructured data, such as text and images, or semi-structured data, like time-series. However, there has been limited attention to structured data, such as tabular data, which, despite its prevalence, remains under-studied due to a lack of clean datasets and insufficient research on the transferability of FMs for various tabular data tasks. In response to this gap, we introduce a framework called TabularFM, which incorporates state-of-the-art methods for developing FMs specifically for tabular data. This includes variations of neural architectures such as GANs, VAEs, and Transformers. We have curated a million of tabular datasets and released cleaned versions to facilitate the development of tabular FMs. We pretrained FMs on this curated data, benchmarked various learning methods on these datasets, and released the pretrained models along with leaderboards for future comparative studies. Our fully open-sourced system provides a comprehensive analysis of the transferability of tabular FMs. By releasing these datasets, pretrained models, and leaderboards, we aim to enhance the validity and usability of tabular FMs in the near future.

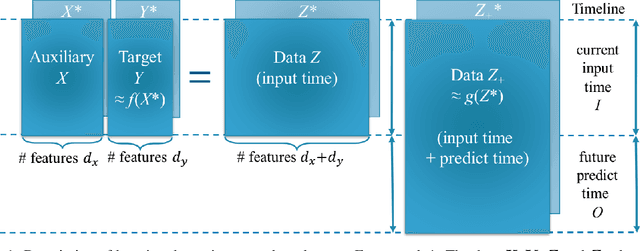
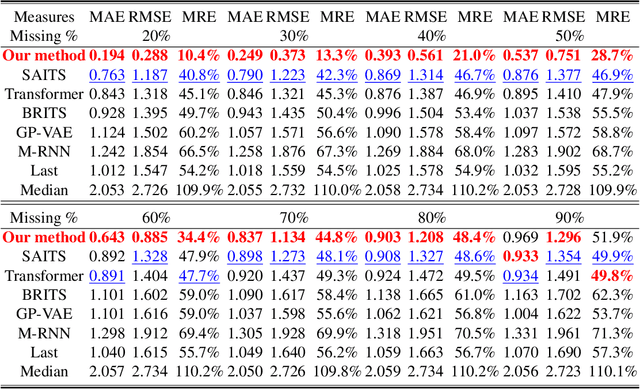
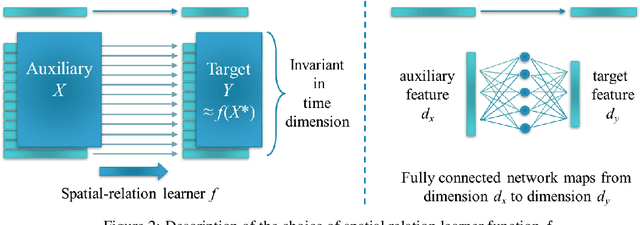
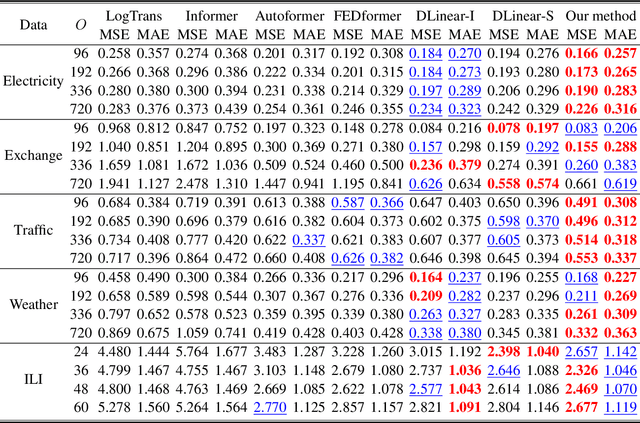
An End-to-End Time Series Model for Simultaneous Imputation and Forecast

Time series forecasting using historical data has been an interesting and challenging topic, especially when the data is corrupted by missing values. In many industrial problem, it is important to learn the inference function between the auxiliary observations and target variables as it provides additional knowledge when the data is not fully observed. We develop an end-to-end time series model that aims to learn the such inference relation and make a multiple-step ahead forecast. Our framework trains jointly two neural networks, one to learn the feature-wise correlations and the other for the modeling of temporal behaviors. Our model is capable of simultaneously imputing the missing entries and making a multiple-step ahead prediction. The experiments show good overall performance of our framework over existing methods in both imputation and forecasting tasks.

Interpretable Clustering via Multi-Polytope Machines

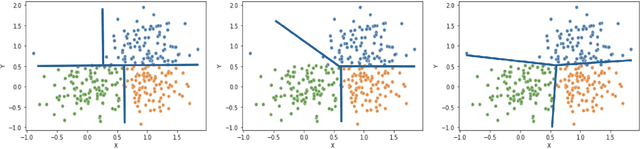
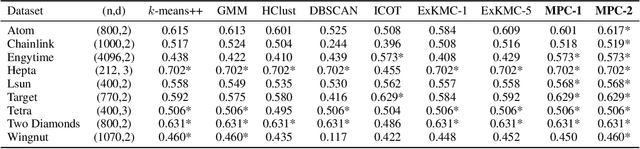
Clustering is a popular unsupervised learning tool often used to discover groups within a larger population such as customer segments, or patient subtypes. However, despite its use as a tool for subgroup discovery and description - few state-of-the-art algorithms provide any rationale or description behind the clusters found. We propose a novel approach for interpretable clustering that both clusters data points and constructs polytopes around the discovered clusters to explain them. Our framework allows for additional constraints on the polytopes - including ensuring that the hyperplanes constructing the polytope are axis-parallel or sparse with integer coefficients. We formulate the problem of constructing clusters via polytopes as a Mixed-Integer Non-Linear Program (MINLP). To solve our formulation we propose a two phase approach where we first initialize clusters and polytopes using alternating minimization, and then use coordinate descent to boost clustering performance. We benchmark our approach on a suite of synthetic and real world clustering problems, where our algorithm outperforms state of the art interpretable and non-interpretable clustering algorithms.

A Scale Invariant Flatness Measure for Deep Network Minima

It has been empirically observed that the flatness of minima obtained from training deep networks seems to correlate with better generalization. However, for deep networks with positively homogeneous activations, most measures of sharpness/flatness are not invariant to rescaling of the network parameters, corresponding to the same function. This means that the measure of flatness/sharpness can be made as small or as large as possible through rescaling, rendering the quantitative measures meaningless. In this paper we show that for deep networks with positively homogenous activations, these rescalings constitute equivalence relations, and that these equivalence relations induce a quotient manifold structure in the parameter space. Using this manifold structure and an appropriate metric, we propose a Hessian-based measure for flatness that is invariant to rescaling. We use this new measure to confirm the proposition that Large-Batch SGD minima are indeed sharper than Small-Batch SGD minima.